4.7. Параметрические цепи.
Это очень интересный и специфический раздел теории цепей. Прежде всего, мы ещё раз вспомним отличие параметрических цепей от нелинейных на простом примере с активным элементом.
Нелинейная
цепь, рис 4.27а. Задано ![]() и
и ![]() (или
(или ![]() ).
Требуется найти
).
Требуется найти ![]() . В такой цепи
. В такой цепи ![]() является функцией искомого тока
(нелинейность). Если ток меняется со временем, то и сопротивление будет
зависеть от времени (через ток).
является функцией искомого тока
(нелинейность). Если ток меняется со временем, то и сопротивление будет
зависеть от времени (через ток).
Параметрическая
линейная цепь, рис. 4.27б. Задано ![]() и
и ![]() . Требуется определить
. Требуется определить ![]() . Сопротивление
. Сопротивление ![]() управляется
не искомым сигналом, а «внешним», не указанным на схеме. Закон изменения
управляется
не искомым сигналом, а «внешним», не указанным на схеме. Закон изменения ![]() задан. Тогда ток в цепи
задан. Тогда ток в цепи ![]() , где
, где ![]() есть
проводимость цепи. Важная особенность параметрических цепей состоит в их
способности преобразовывать спектр входного сигнала так, что в спектре тоже
появляются новые частоты, как в нелинейных цепях. Именно это обстоятельство я и
хочу проиллюстрировать на нескольких простых примерах.
есть
проводимость цепи. Важная особенность параметрических цепей состоит в их
способности преобразовывать спектр входного сигнала так, что в спектре тоже
появляются новые частоты, как в нелинейных цепях. Именно это обстоятельство я и
хочу проиллюстрировать на нескольких простых примерах.
Мы совершенно не будем затрагивать интересные вопросы параметрического усиления и генерирования, проблемы устойчивости таких цепей, это выходит за рамки курса.
В
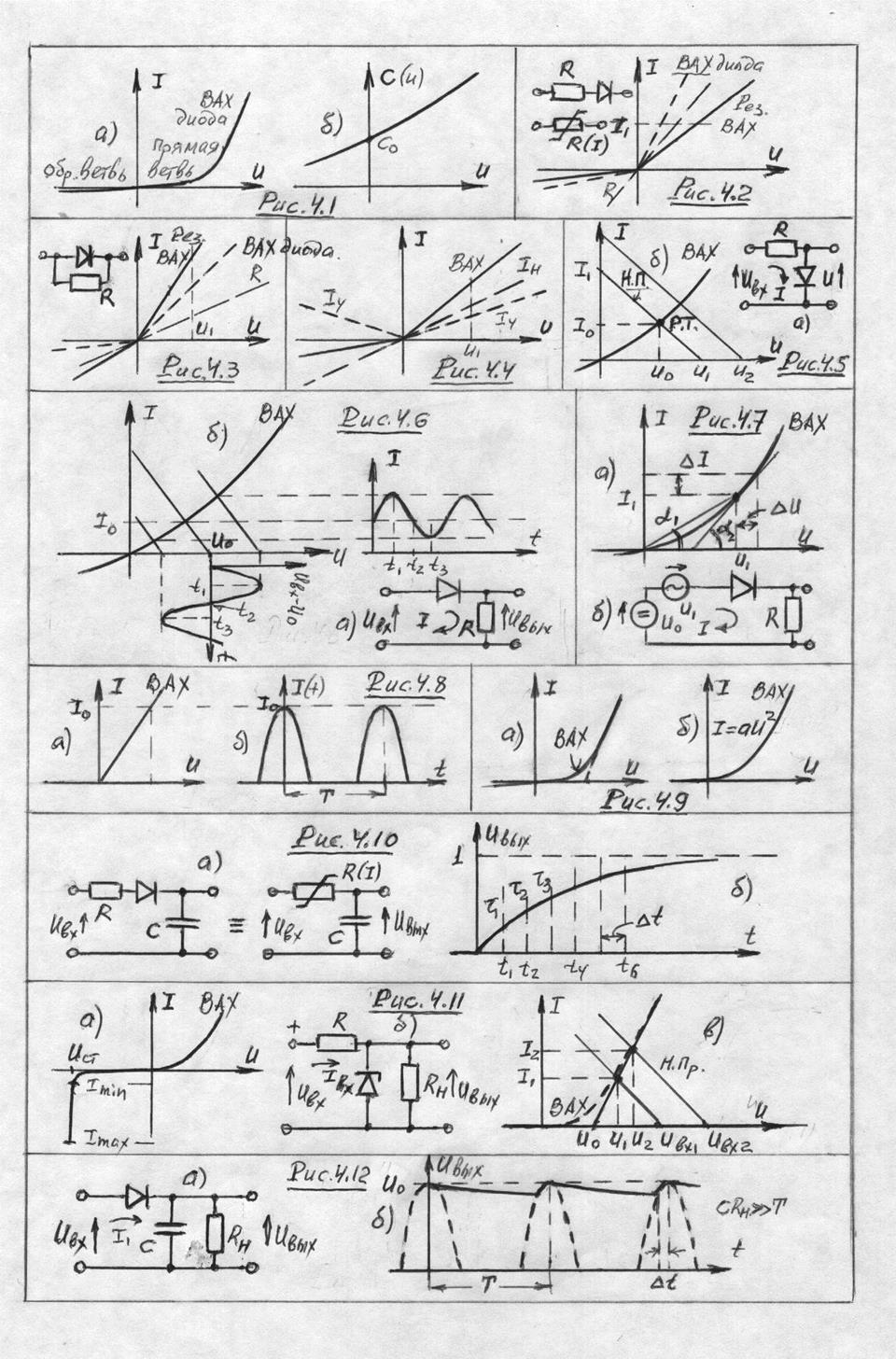
качестве первого примера рассмотрим цепь с ключом, рис. 4.28. ![]() , когда ключ замкнут, и
, когда ключ замкнут, и ![]() , когда ключ разомкнут.
, когда ключ разомкнут. ![]() . Закон изменения
. Закон изменения ![]() задан
и изображён на рис. 4.29. Там же приведён и результат. В первом случае, рис.
4.29а, получили синхронное выпрямление, всё как при ограничении сигнала диодом.
Появилась постоянная составляющая
задан
и изображён на рис. 4.29. Там же приведён и результат. В первом случае, рис.
4.29а, получили синхронное выпрямление, всё как при ограничении сигнала диодом.
Появилась постоянная составляющая ![]() и гармоники частоты
и гармоники частоты ![]() . В схеме ограничителя с диодом проводимость
диода управляется входным напряжением. Ток течёт только тогда, когда
. В схеме ограничителя с диодом проводимость
диода управляется входным напряжением. Ток течёт только тогда, когда ![]() . Диод тоже работает как ключ.
. Диод тоже работает как ключ.
В
параметрической цепи проводимостью управляет внешний сигнал. Поэтому появляется
новая возможность. Сместим функцию ![]() на четверть периода
вправо, рис. 4.29б. Постоянная составляющая тока исчезла, но гармоники частоты
на четверть периода
вправо, рис. 4.29б. Постоянная составляющая тока исчезла, но гармоники частоты ![]() остались. Такая схема может служить
фазовым детектором. В реальных схемах роль управляемого ключа играют
транзисторы.
остались. Такая схема может служить
фазовым детектором. В реальных схемах роль управляемого ключа играют
транзисторы.
Вернёмся
к схеме на рис. 4.27б. Для неё ![]() . Значит эта простая
схема с параметрической проводимостью
. Значит эта простая
схема с параметрической проводимостью ![]() может
обеспечить перемножение сигналов
может
обеспечить перемножение сигналов ![]() и
и ![]() без нелинейных элементов. Цепь получается
линейной. Следовательно, такие операции как преобразование несущей частоты, модуляция,
синхронное детектирование, которые сводятся к перемножению сигналов, могут быть
реализованы без нелинейных элементов. Понятно, что это сложная задача. Только
на бумаге всё делается очень легко. Практически реализовать достаточно линейный
перемножитель совсем не просто, но можно.
без нелинейных элементов. Цепь получается
линейной. Следовательно, такие операции как преобразование несущей частоты, модуляция,
синхронное детектирование, которые сводятся к перемножению сигналов, могут быть
реализованы без нелинейных элементов. Понятно, что это сложная задача. Только
на бумаге всё делается очень легко. Практически реализовать достаточно линейный
перемножитель совсем не просто, но можно.
Приведём
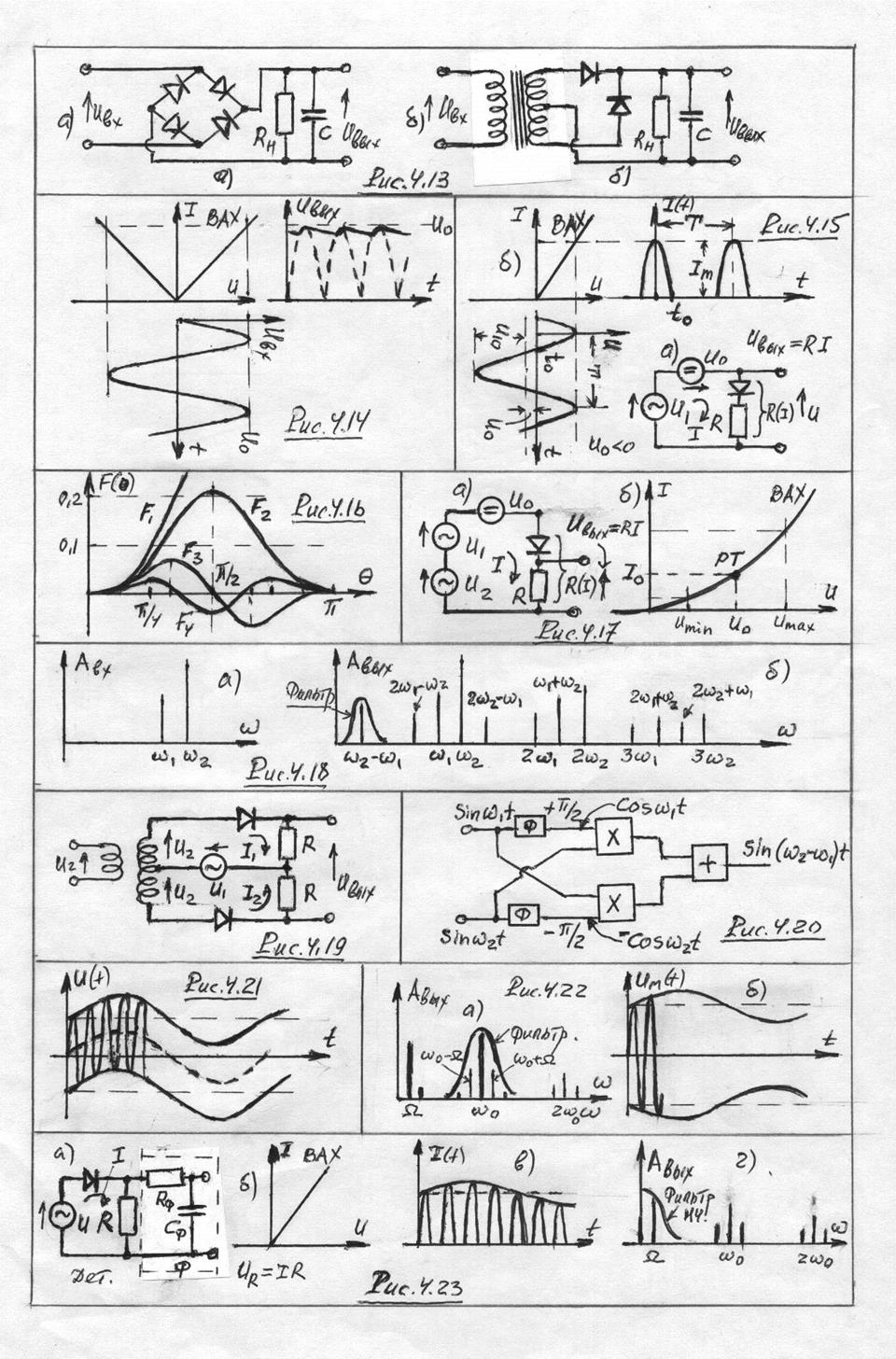
пример реализации параметрического модулятора. Пусть ![]() ,
а
,
а ![]() . Тогда
. Тогда ![]() ,
, ![]() . Получили чистую модуляцию. Не надо
никаких фильтров. Вся проблема заключается теперь в реализации нужной
зависимости
. Получили чистую модуляцию. Не надо
никаких фильтров. Вся проблема заключается теперь в реализации нужной
зависимости ![]() . Надо научиться управлять проводимостью с
помощью электрического сигнала. Приведём один из вариантов такого устройства.
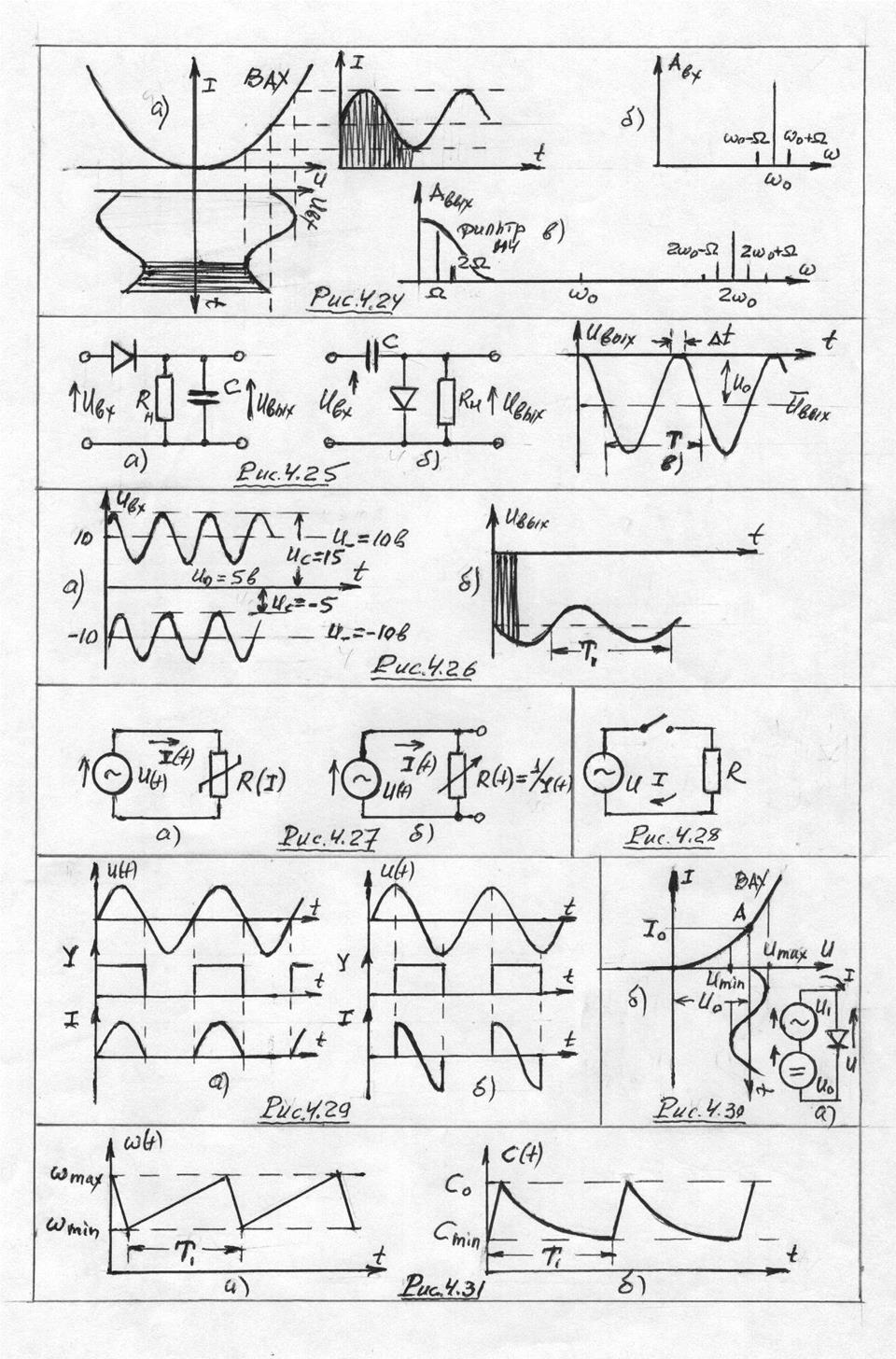
На рис. 4.30 изображена схема и ВАХ диода.
. Надо научиться управлять проводимостью с
помощью электрического сигнала. Приведём один из вариантов такого устройства.
На рис. 4.30 изображена схема и ВАХ диода. ![]() .
Постоянное напряжение
.
Постоянное напряжение ![]() определяет рабочую точку А на
ВАХ диода.
определяет рабочую точку А на
ВАХ диода. ![]() . Определим дифференциальную проводимость
диода
. Определим дифференциальную проводимость
диода ![]() в малой окрестности рабочей точки. Если на
этом выделенном малом участке ВАХ
в малой окрестности рабочей точки. Если на
этом выделенном малом участке ВАХ ![]() , то
, то ![]() , т.е. будет меняться пропорционально
, т.е. будет меняться пропорционально ![]() . Осталось совместить две рассмотренные
цепи. Можно и это сделать, но на этом мы останавливаться уже не будем.
. Осталось совместить две рассмотренные
цепи. Можно и это сделать, но на этом мы останавливаться уже не будем.
Последний
пример касается получения сигналов, частота которых периодически меняется по линейному
закону (ЛЧМ сигналы). Они получили широкое применение. Частоту колебаний
высокочастотного генератора обычно определяет колебательный контур. Чтобы
изменить его резонансную частоту, надо менять индуктивность или ёмкость. Будем
менять ![]() . Мы хотим обеспечить медленное, по
сравнению с периодом колебаний
. Мы хотим обеспечить медленное, по
сравнению с периодом колебаний ![]() , возрастание частоты по
линейному закону
, возрастание частоты по
линейному закону ![]() на периоде
на периоде ![]() , рис. 4.31а. Пусть
, рис. 4.31а. Пусть ![]() .
Искомая зависимость
.
Искомая зависимость ![]() определяется из следующего равенства:
определяется из следующего равенства:
![]() .
. ![]() .
Результат изображён качественно на рис. 4.31б. Надо реализовать такой закон
изменения ёмкости и мы получим ЛЧМ сигнал.
.
Результат изображён качественно на рис. 4.31б. Надо реализовать такой закон
изменения ёмкости и мы получим ЛЧМ сигнал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.