Генераторы. Генератор пилообразных импульсов. Генератор гармонических колебаний с обратной связью. Метод фазовой плоскости, страница 4

Мощные генераторы для увеличения КПД часто работают с «отсечкой» тока. Транзистор открывается в некоторый оптимальный момент только на короткое время (малую часть периода), чтобы осуществить подпитку контура энергией.

Стабильность частоты является очень важной характеристикой генератора. Чем определяется стабильность частоты? Она определяется добротностью колебательной системы генератора. Чем больше добротность, тем лучше стабильность частоты. Стабильность оценивается по относительным изменениям частоты и составляет для обычных генераторов величину порядка .

7.2.1. Генератор с контуром в цепи стока.

Проиллюстрируем на этом примере, рис. 7.13, другой способ рассуждений для получения условий возбуждения. Рассмотрим это устройство как усилитель с обратной связью и применим общую формулу . Здесь  есть коэффициент усиления без обратной связи, а  - коэффициент передачи цепи обратной связи. Неустойчивость, возбуждение возникает тогда, когда . Это комплексное в общем случае условие часто записывают в виде двух вещественных равенств: 1. «Баланс» фаз, ; 2. «Баланс» амплитуд, .

Рассуждают следующим образом. Разомкнём цепь обратной связи и определим произведение , считая, что на вход транзистора поступает некоторое «внешнее» напряжение . Сначала определяем напряжение на контуре. . Здесь:  - динамическая крутизна транзистора;  - комплексное сопротивление контура; ; ; . Нас интересует напряжение на резонансной частоте , когда . Тогда сопротивление контура активно и коэффициент усиления без обратной связи . Теперь определяем ток в индуктивной ветви контура, считая , и напряжение обратной связи. ; . Наконец, коэффициент передачи цепи обратной связи, . Знак минус соответствует положительной обратной связи. В результате имеем: . Напряжения  и  оказываются синфазными (положительная связь). Надлежащим выбором параметров может быть реализовано условие , т.е. . Это и есть условие возбуждения. Замыкая цепь обратной связи, мы получим генератор. «Внешнее» напряжение  больше не нужно.

Условия возбуждения оказались одинаковыми, независимо от того, в какой цепи транзистора стоит колебательный контур. На практике широко используется автотрансформаторная схема подключения цепи обратной связи к контуру, изображённая на рис. 7.14.

7.3. Метод медленно меняющихся амплитуд.

Вернёмся к вопросу установления амплитуды колебаний в генераторах с колебательным контуром и изложим коротко идею названного метода решения нелинейного дифференциального уравнения  . Здесь: . Нелинейность проявляется через параметр .

Если  считать постоянным, то уравнение линейно. Соответствующее характеристическое уравнение  имеет корни , где 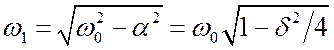 есть частота, на которой контур «звучит». Обычно, если добротность , то . Будем считать эти неравенства выполненными. Решение дифференциального уравнения есть комбинация функций . При этом амплитуда колебаний  меняется гораздо медленнее, чем осциллирующий множитель . .

Учтём изложенные соображения и вернёмся к нелинейному уравнению. Будем сразу искать его решение в виде произведения . Добротность считаем большой (), . Относительное изменение амплитуды за период мало (). Вычисляем производные: ; . Подставляя их в дифференциальное уравнение, получим . Оставим в этом уравнении только главные члены, второй и четвёртый, имеющие порядок . Два другие члена имеют порядок . В результате, получили более простое нелинейное уравнение первого порядка для амплитудной функции. . Параметр  этого уравнения есть заданная функция амплитуды, через вносимое сопротивление и среднюю крутизну.

На этом можно было и закончить изложение метода медленно меняющихся амплитуд. Дальше надо решать это уравнение. Общий характер решения очевиден из энергетических соображений и изображён на рис. 7.15. Это мы уже подробно обсуждали. Однако, вернёмся к этому вопросу ещё раз.

Пусть рабочая точка выбрана на участке с максимальной крутизной  (точка  на рис. 7.10) и условие возбуждения для этой точки выполнено. Тогда . Реализован «мягкий» режим возбуждения. При очень малых амплитудах мы можем считать уравнение линейным, поскольку  и постоянно, и написать его решение. . Дальше используется такой типичный алгоритм приближенного решения нелинейного уравнения для . Весь интересующий нас временной интервал разбивается на промежутки, в пределах которых мы решаем уравнение, как линейное, с некоторым постоянным значением , определённым по амплитуде предыдущего шага (квазилинейный подход, амплитуда меняется медленно). Тогда, на промежутке , .