4. ДИСКРЕТИЗАЦИЯ РАДИОСИГНАЛОВ
Дискретизация радиосигналов на основе теоремы Котельникова
Дискретизация – представление непрерывного (аналогового) сигнала дискретной последовательностью отсчетов, по которым с заданной точностью можно восстановить исходный аналоговый сигнал.
Теорема Котельникова:
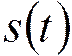 - сигнал
- сигнал
![]() - верхняя граничная частота спектра
сигнала
- верхняя граничная частота спектра
сигнала
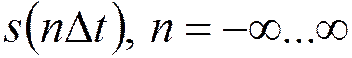 - отсчеты через интервал времени
- отсчеты через интервал времени 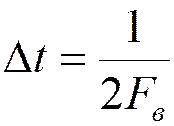
Ряд Котельникова:
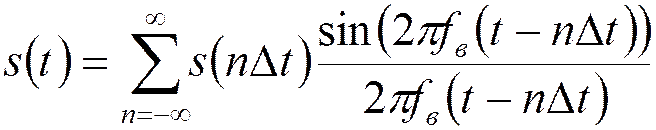
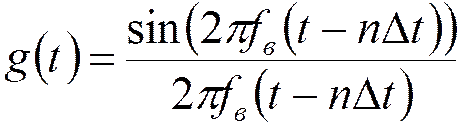 - импульсная характеристика ФНЧ
с полосой пропускания
- импульсная характеристика ФНЧ
с полосой пропускания ![]() .
.
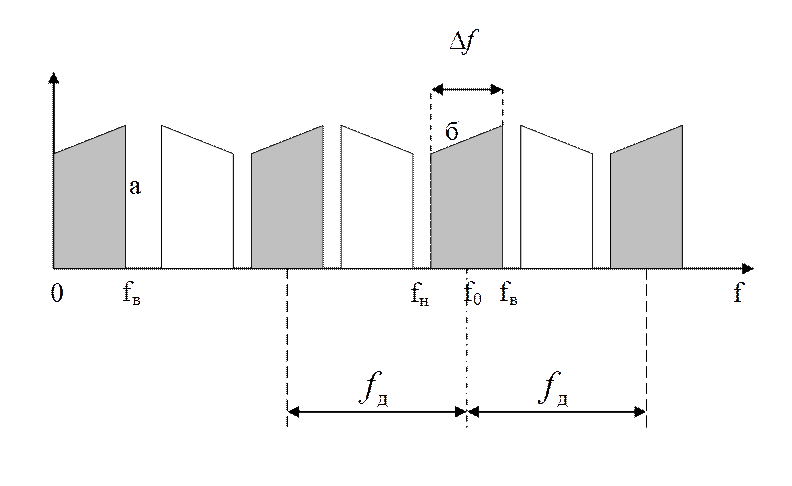
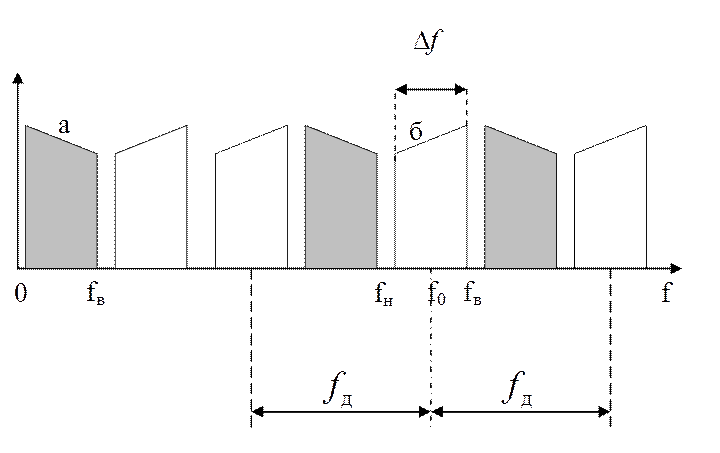
Частота дискретизации НЧ сигналов: 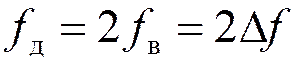
Частота дискретизации полосовых сигналов: 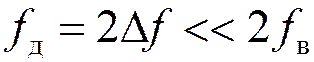
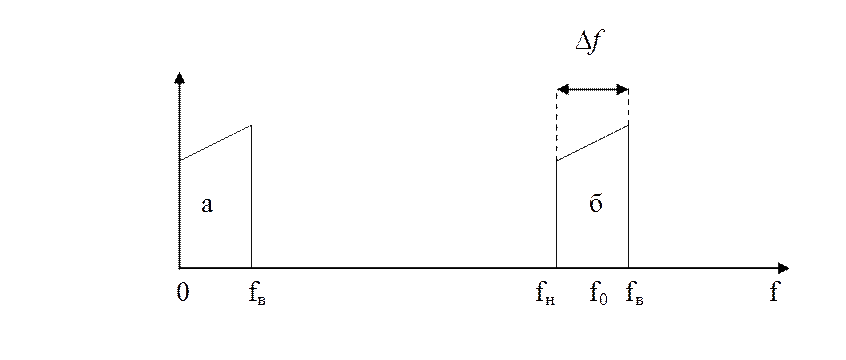
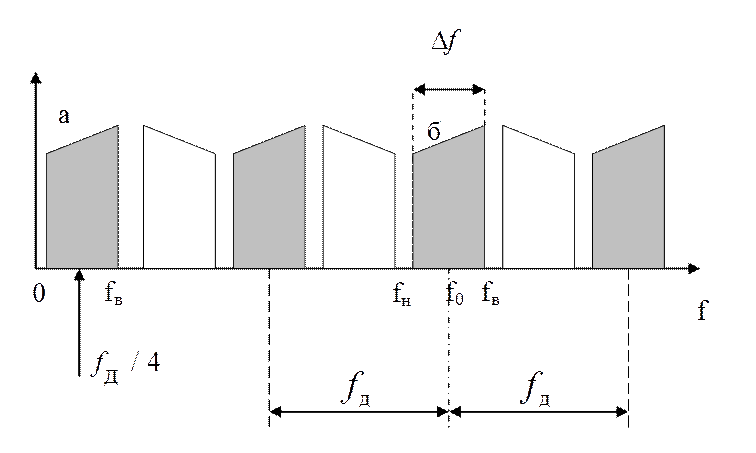
а б
Спектры низкочастотного а) и полосового б) сигналов
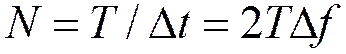 - число отсчетов на интервале времени
- число отсчетов на интервале времени ![]()
Ряд Котельникова для полосового сигнала:
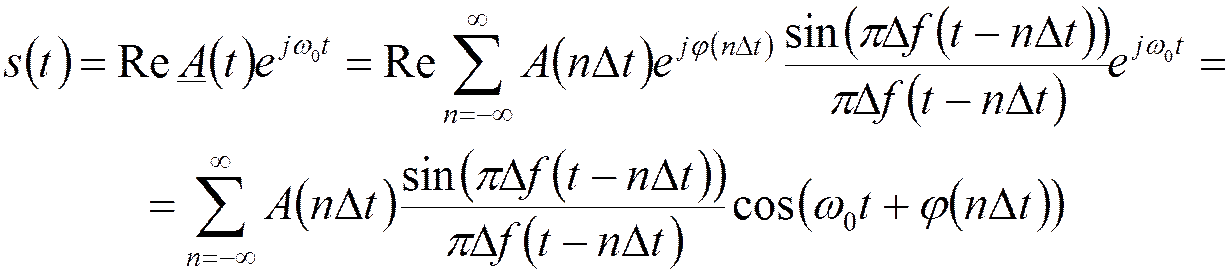
 - полоса частот радиосигнала,
- полоса частот радиосигнала,
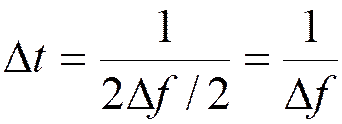 - интервал дискретизации
- интервал дискретизации
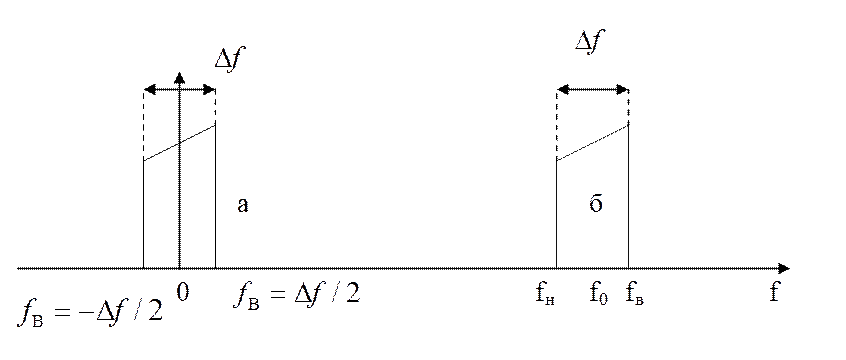
а б
Спектры комплексной огибающей а) и исходного радиосигнала б)
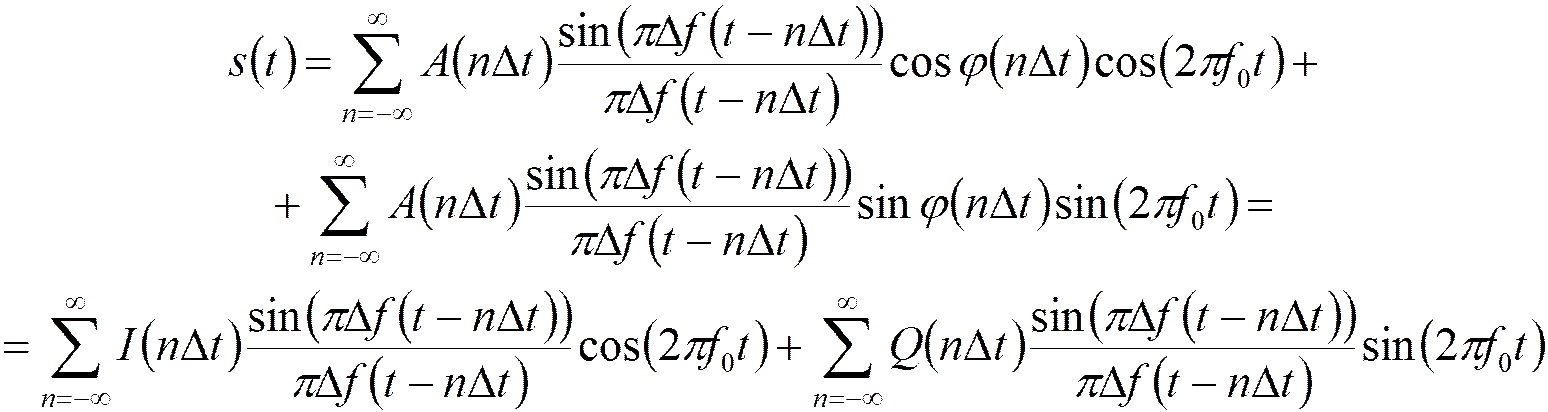
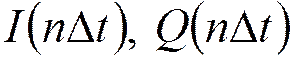 - синфазная и квадратурная составляющие
- синфазная и квадратурная составляющие
Микроуровневая дискретизация
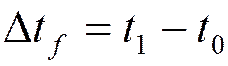 - интервал времени от момента
стробирования
- интервал времени от момента
стробирования ![]() до момента первого
до момента первого ![]() положительного перехода через ноль
положительного перехода через ноль
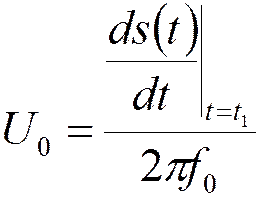 - амплитуда гармонического колебания
- амплитуда гармонического колебания
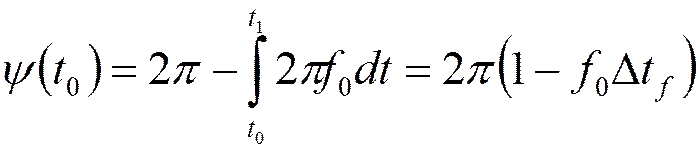 - фаза гармонического колебания
- фаза гармонического колебания
Стробирование радиосигналов
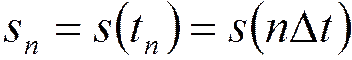 - отсчет сигнала
- отсчет сигнала
![]() - момент времени взятия отсчета
- момент времени взятия отсчета
Источники погрешностей при стробировании:
- время стробирования и хранения
- скорость изменения сигнала во времени
Время стробирования и хранения.
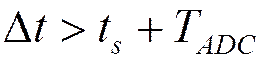 - временной цикл дискретизации состоит из
следующих этапов:
- временной цикл дискретизации состоит из
следующих этапов:
![]() - время стробирования,
- время стробирования,
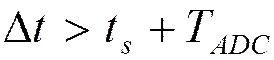 - время аналого-цифрового преобразования.
- время аналого-цифрового преобразования.
Типы устройств выборки-хранения (УВХ):
- следящий
- интегрирующий 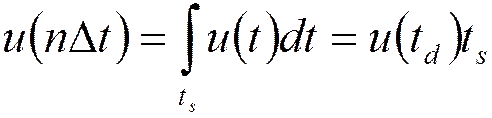
Ошибка за счет длительности строба
Критерий выбора
длительности строба: 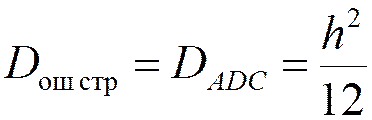 .
.
Двуполярный синусоидальный сигнал с частотой ![]() :
: 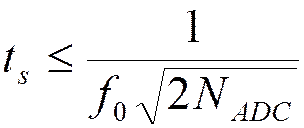
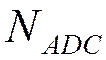 – полное число уровней квантования.
– полное число уровней квантования.
Влияние ширины спектра сигнала на ошибку стробирования:
Наихудший случай
– спектр сосредоточен на границе полосы частот  :
:
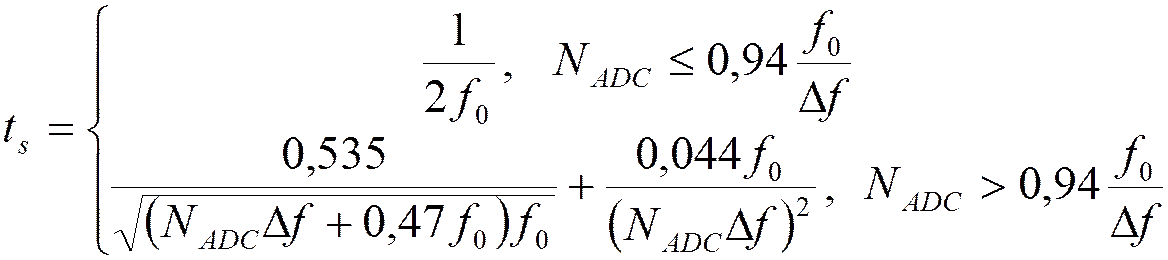
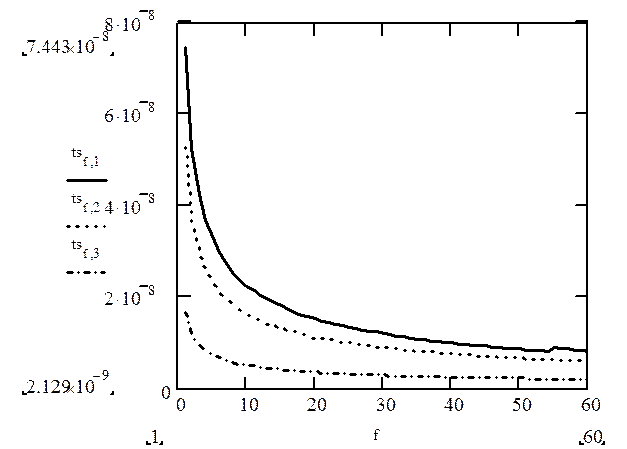 МГц
МГц
Зависимость длительности строба от несущей частоты сигнала
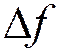 =50 кГц – сплошная линия
=50 кГц – сплошная линия
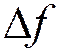 =100 кГц – пунктирная
линия
=100 кГц – пунктирная
линия
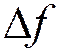 =1 МГц – штрих-пунктирная
линия
=1 МГц – штрих-пунктирная
линия
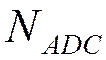 =1024.
=1024.
Метод устранения ограничения 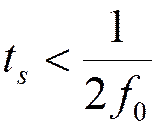
Метод радиоимпульсного стробирования:
радиоимпульс частотой ![]() , длительностью
, длительностью 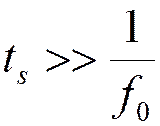
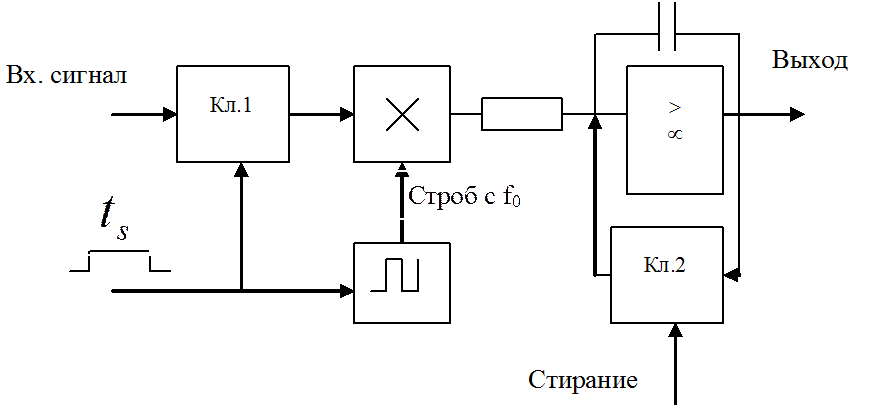
Пусть на вход поступает гармонический сигнал с частотой ![]() :
: 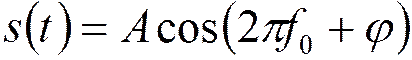 .
.
Результат интегрирования за время 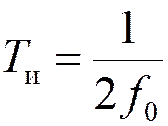 :
:
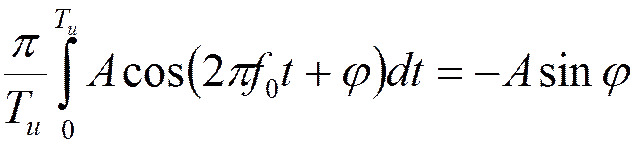
Время стробирования: 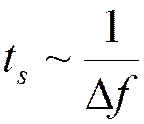 .
.
Двухканальные устройства дискретизации радиосигналов
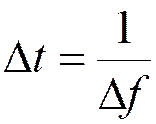 - интервал дискретизации
- интервал дискретизации
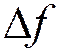 - ширина спектра радиосигнала
- ширина спектра радиосигнала
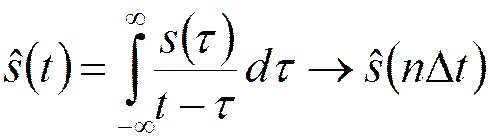
Преобразование Гильберта для узкополосного сигнала:
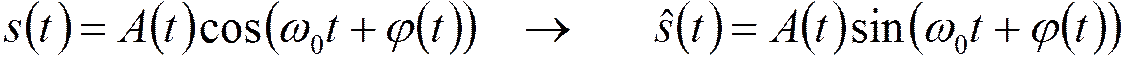
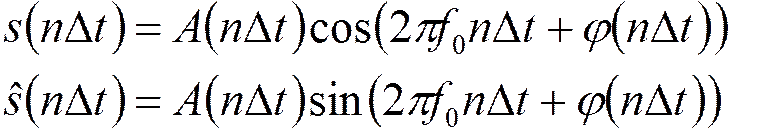
Используем за основу ряд Котельникова для узкополосных сигналов:
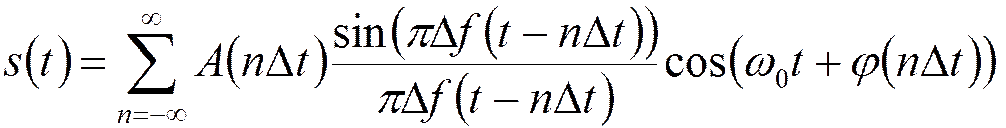
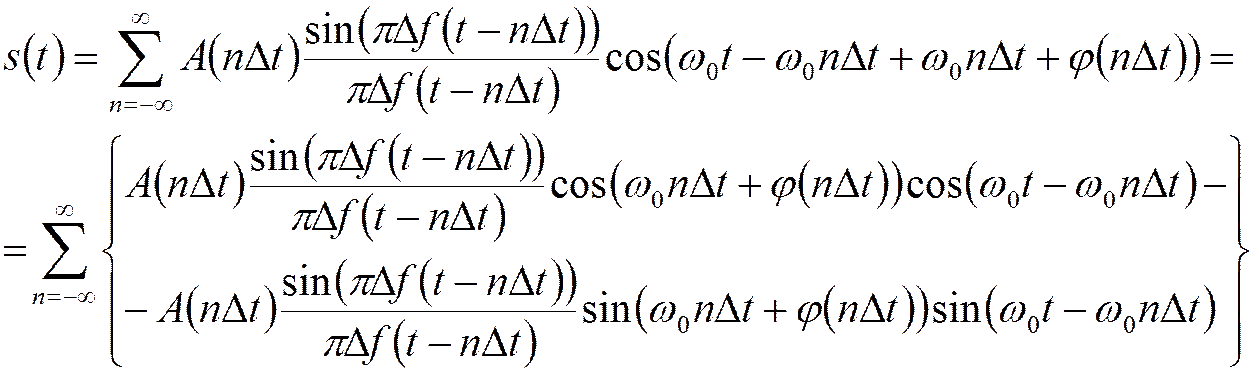
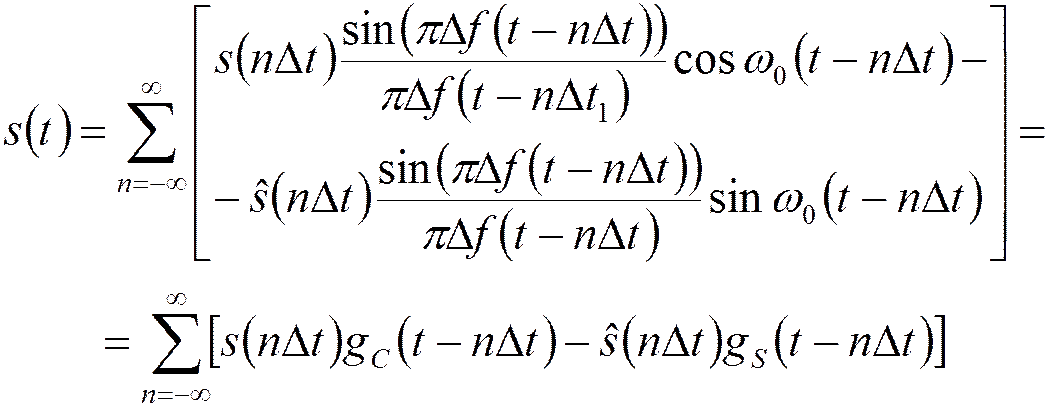
импульсные характеристики полосовых фильтров:
Двухканальная дискретизация → ограничение на соотношение между ![]() и
и ![]() отсутствуют
отсутствуют
Одноканальная дискретизация радиосигналов
Дискретизация = амплитудно-импульсная модуляция
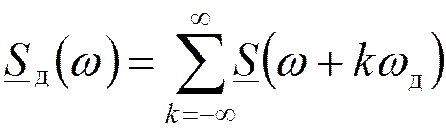 - спектр дискретного
радиосигнала
- спектр дискретного
радиосигнала
Спектр дискретного радиосигнала
РАЦИОНАЛЬНАЯ дискретизация: отсутствует наложение спектральных образов :
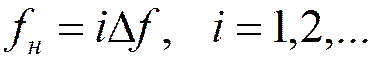 ,
, 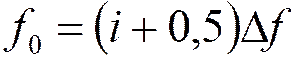
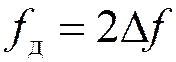
ОПТИМАЛЬНАЯ дискретизация: отсутствует наложение спектральных образов, обеспечивается одинаковый защитный интервал между спектральными образами
Внимание ! Величина защитного интервала включена в значение ширины спектра сигнала.
Вариант 1. Частота
гармоники частоты дискретизации, ближайшей к спектру исходного сигнала 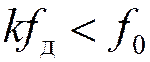 . При этом самый низкочастотный
спектральный образ дискретного сигнала является неинвертированным по частоте по
отношению к спектру исходного сигнала.
. При этом самый низкочастотный
спектральный образ дискретного сигнала является неинвертированным по частоте по
отношению к спектру исходного сигнала.
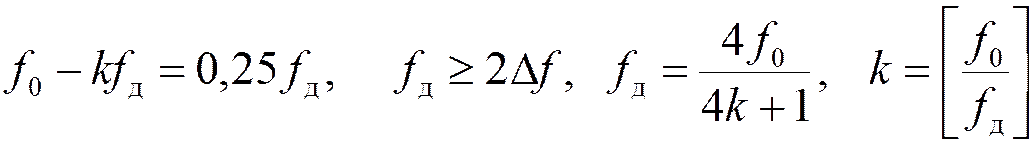
где квадратные скобки означают усечение до целого числа
Алгоритм расчета оптимальной частоты дискретизации:
1) 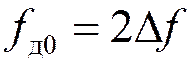 - нулевое приближение частоты
дискретизации
- нулевое приближение частоты
дискретизации
2) 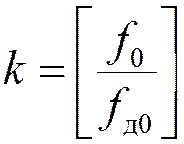 - номер гармоники спектрального
образа, наиболее близкого к спектру исходного сигнала
- номер гармоники спектрального
образа, наиболее близкого к спектру исходного сигнала
3) 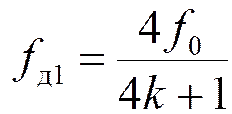 - первое приближение частоты
дискретизации
- первое приближение частоты
дискретизации
4) если 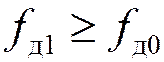 , то расчет окончен, если
, то расчет окончен, если 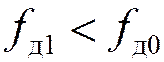 , то
, то 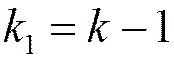 и
расчет повторяется с п.3
и
расчет повторяется с п.3
Пример 1. ![]() =1000 кГц,
=1000 кГц, 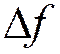 =150
кГц.
=150
кГц.
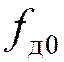 =2*150=300 кГц.
=2*150=300 кГц.
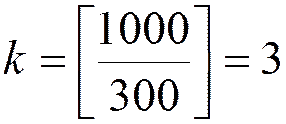 .
.
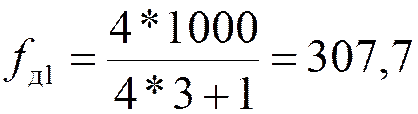 кГц.
кГц.
Так как 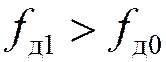 , то
, то 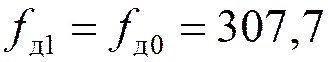 кГц
кГц
Вариант 2. Частота
гармоники частоты дискретизации, ближайшей к спектру исходного сигнала 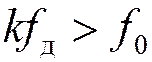 . При этом самый низкочастотный
спектральный образ дискретного сигнала является инвертированным по частоте по отношению
к спектру исходного сигнала.
. При этом самый низкочастотный
спектральный образ дискретного сигнала является инвертированным по частоте по отношению
к спектру исходного сигнала.
В этом случае алгоритм определения частоты дискретизации аналогичен, но формулы несколько другие:
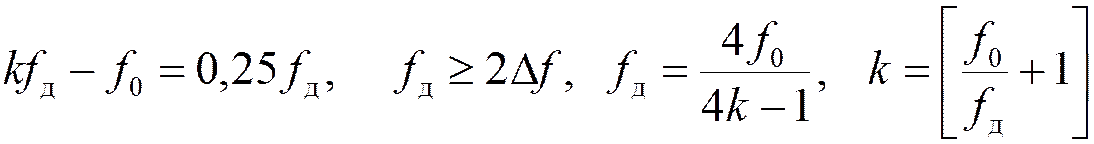 ,
,
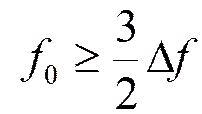 .
.
Пример. ![]() =1000 кГц,
=1000 кГц, 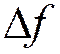 =150
кГц.
=150
кГц.
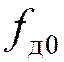 =2*150=300 кГц.
=2*150=300 кГц.
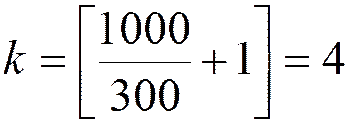 .
.
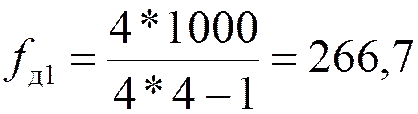 кГц.
кГц.
Так как 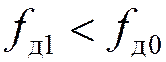 , то
, то 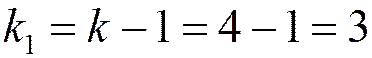
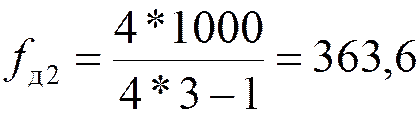 кГц
кГц
Так как 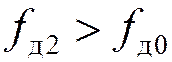 , то
, то 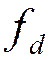 =363,6 кГц.
=363,6 кГц.
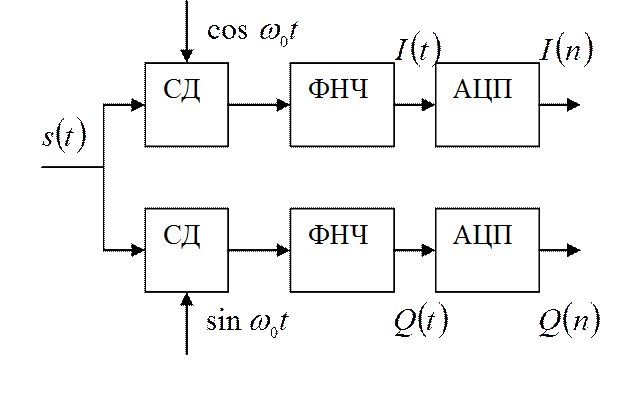
Формирование квадратурных составляющих радиосигналов
1. Двухканальная дискретизация радиосигнала на основе преобразования Гильберта;
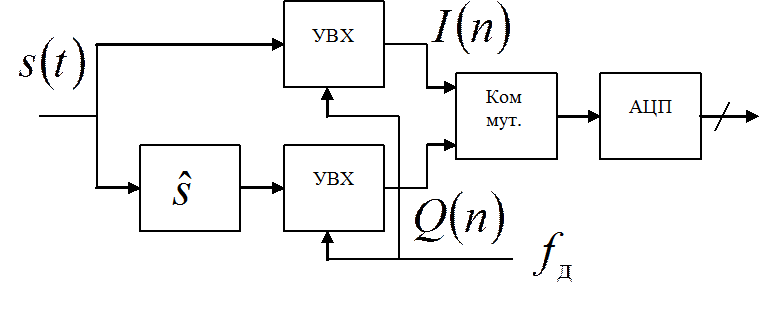
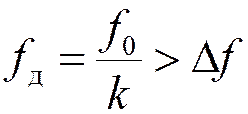
Дискретизация в этом случае поясняется следующими формулами:
а) в основном канале:
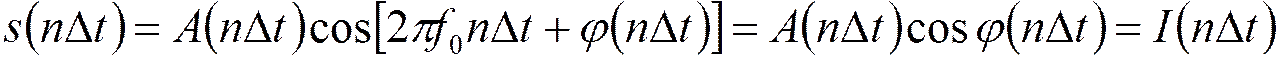 ;
;
б) в канале преобразования Гильберта:
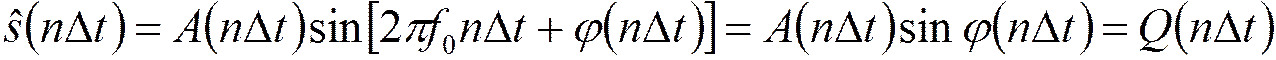 ;
;
2. Двухканальная дискретизация сигналов с выходов смесителей
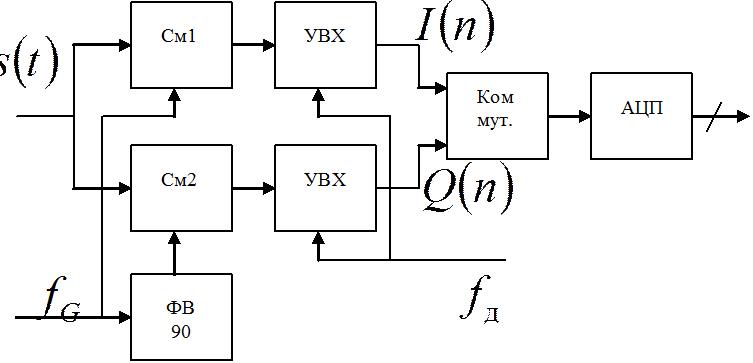
а) 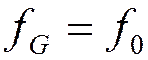 → синхронное детектирование,
полоса частот ФНЧ
→ синхронное детектирование,
полоса частот ФНЧ 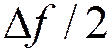
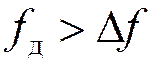
б) 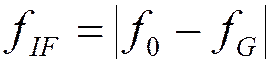 ,
,
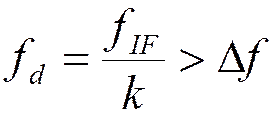
Преобразование Гильберта с помощью преобразователей частоты
а)_в канале 0°:
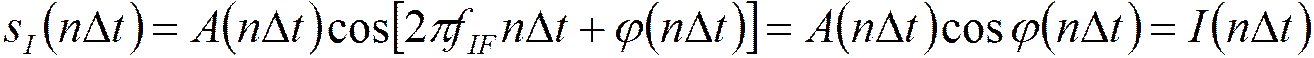 ;
;
б) в канале 90°:
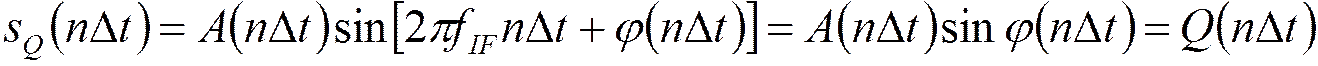 .
.
3. Двухканальная дискретизация, с использованием отсчетных
импульсов, задержанных относительно друг друга на четверть периода несущего
колебания 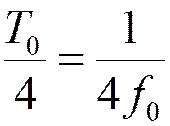 ,
, 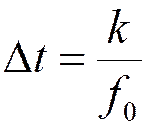 .
.
а) 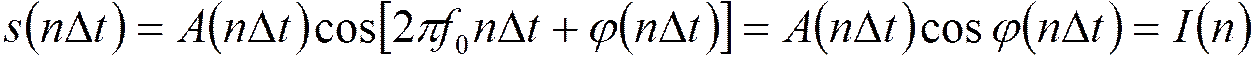
б) 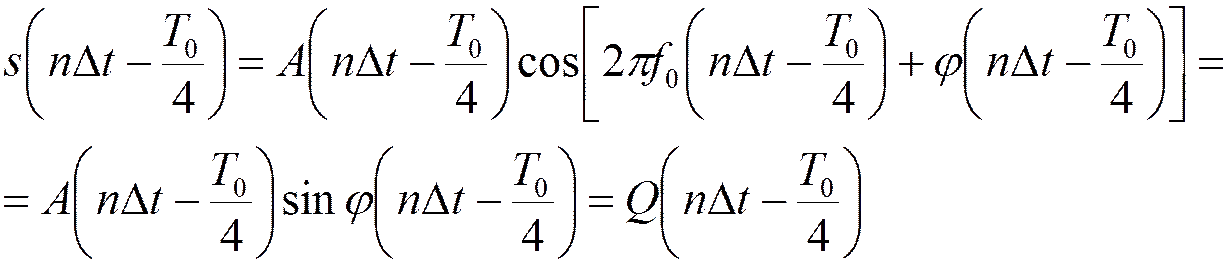
Для совмещения во времени отсчетов
квадратурных сигналов  требуется
интерполяция с помощью линейного интерполирующего фильтра.
требуется
интерполяция с помощью линейного интерполирующего фильтра.
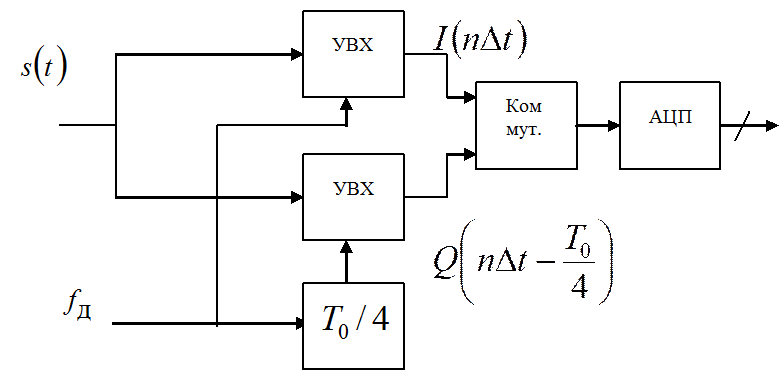
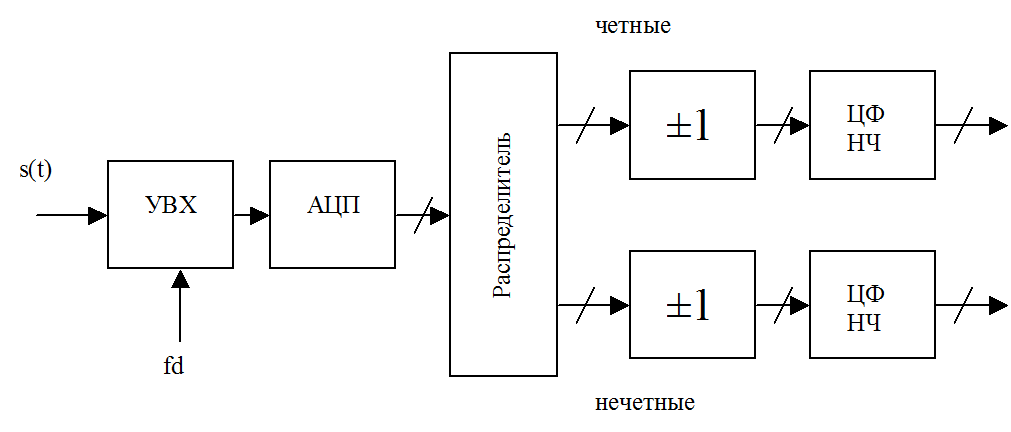
4. Одноканальная дискретизация радиосигналов
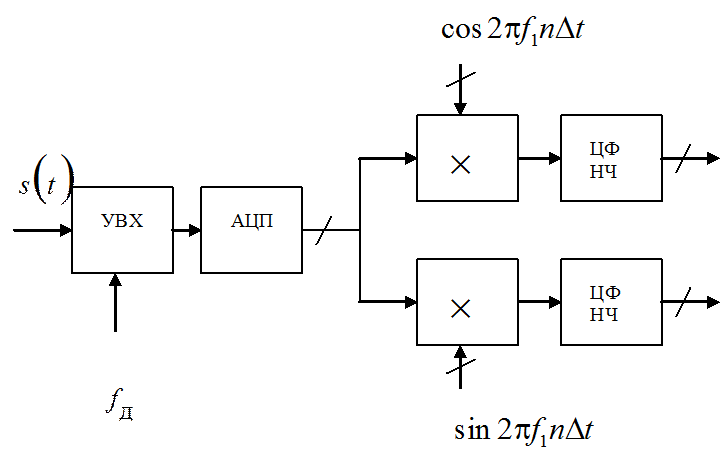
Последовательность отсчетов умножается на 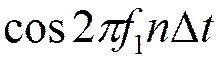 и
и
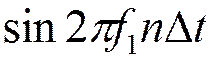 , где
, где 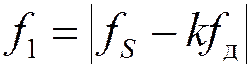 -
центральная частота самого низкочастотного отображения спектра полосового
сигнала,
-
центральная частота самого низкочастотного отображения спектра полосового
сигнала, ![]() – номер ближайшей к
– номер ближайшей к ![]() гармоники частоты
гармоники частоты ![]() .
.

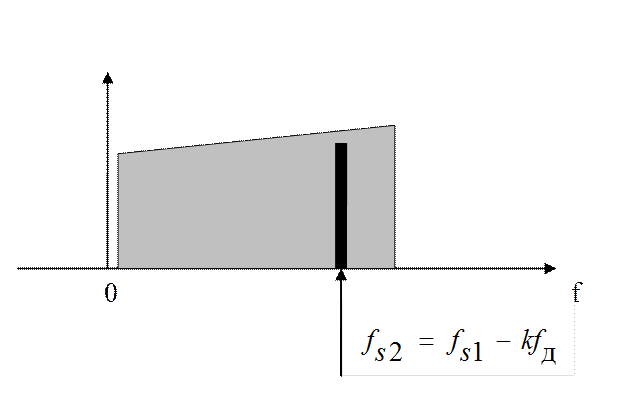
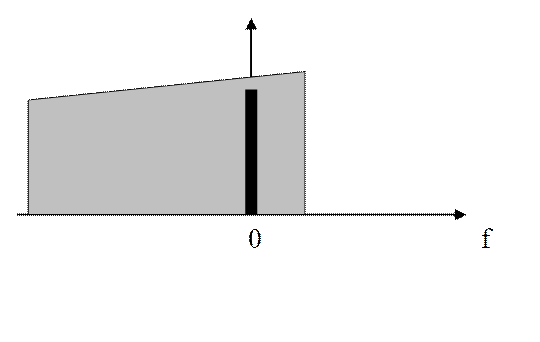
Спектры сигнала после преобразования в цифровом смесителе
Частный случай:
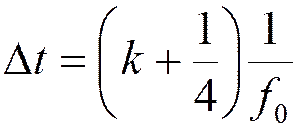 при
при 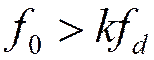
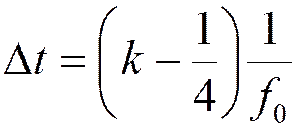 при
при 
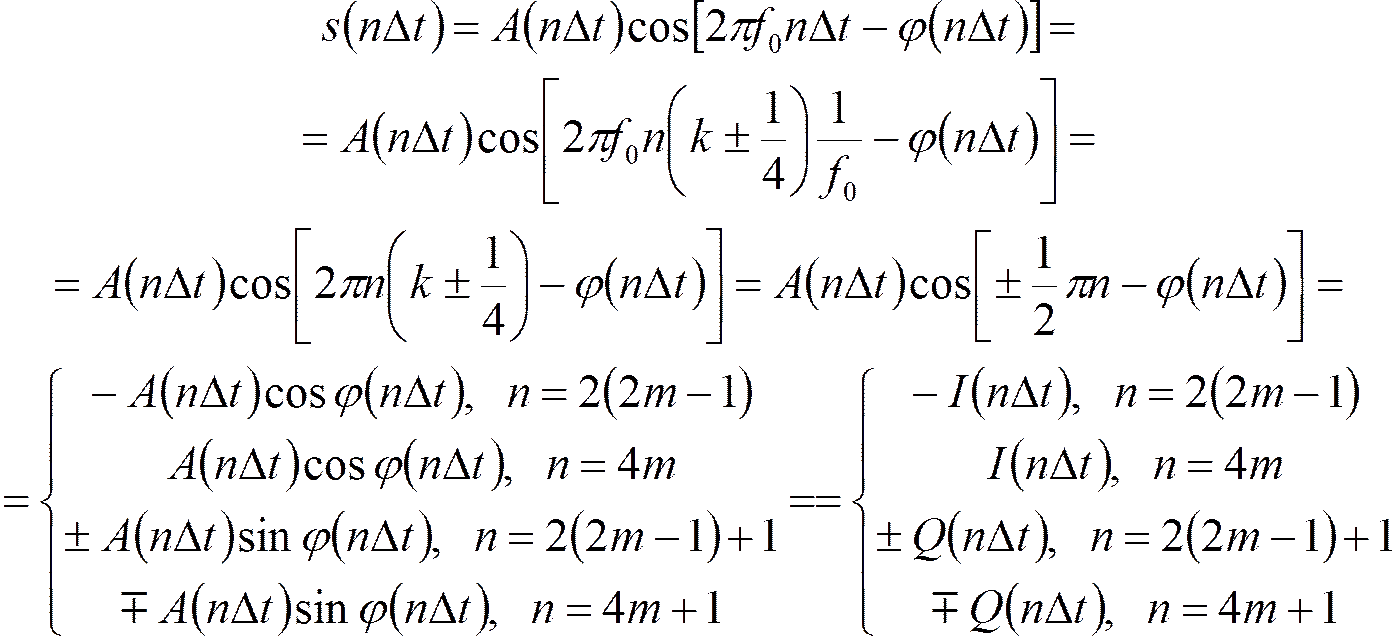
Восстановление сигнала:
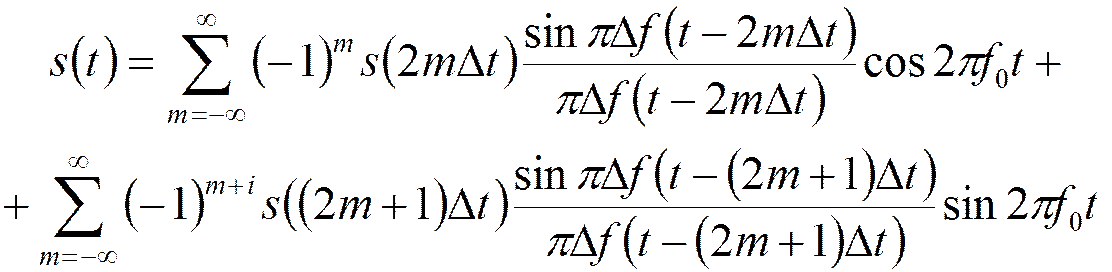 ,
,
где ![]() при
при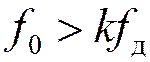 ,
, ![]() при
при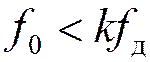 .
.
Аналогичный результат можно получить, если 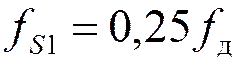 .
.
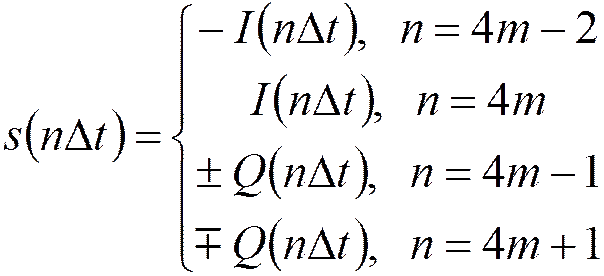
Требуется интерполяция:
Теорема Найквиста
Если синхронные короткие импульсы с
частотой следования ![]() подаются в канал, имеющий
идеальную прямоугольную АЧХ с частотой среза
подаются в канал, имеющий
идеальную прямоугольную АЧХ с частотой среза 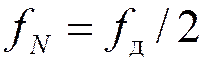 , то
отклики на эти импульсы можно наблюдать независимо, т.е. без межсимвольной
интерференции.
, то
отклики на эти импульсы можно наблюдать независимо, т.е. без межсимвольной
интерференции.

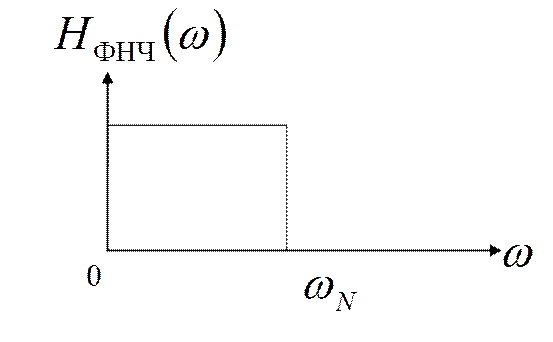
Применение амплитудного корректора
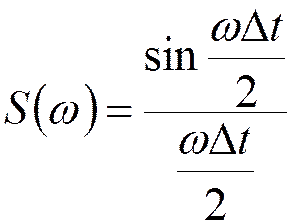 - спектр возбуждающих
импульсов АИМ
- спектр возбуждающих
импульсов АИМ
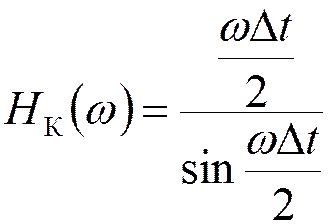 - АЧХ
амплитудного корректора
- АЧХ
амплитудного корректора
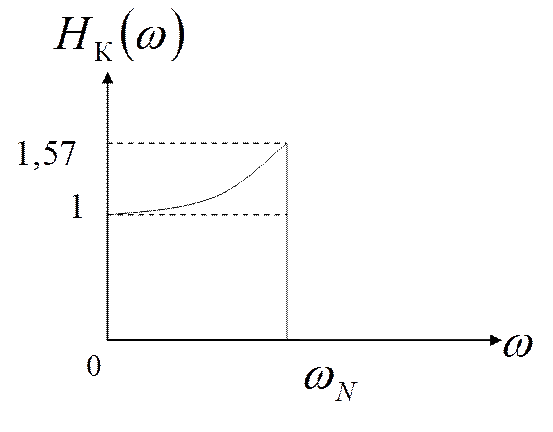
Теорема Найквиста о частичной симметрии.
Суммирование 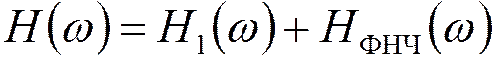 действительной
кососимметричной функции передачи
действительной
кососимметричной функции передачи 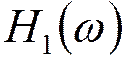 с характеристикой
передачи идеального ФНЧ
с характеристикой
передачи идеального ФНЧ 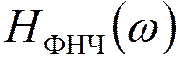 сохраняет моменты
пересечения импульсной характеристики с нулевой осью.
сохраняет моменты
пересечения импульсной характеристики с нулевой осью.
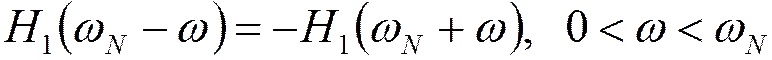 - свойство кососимметрии
- свойство кососимметрии
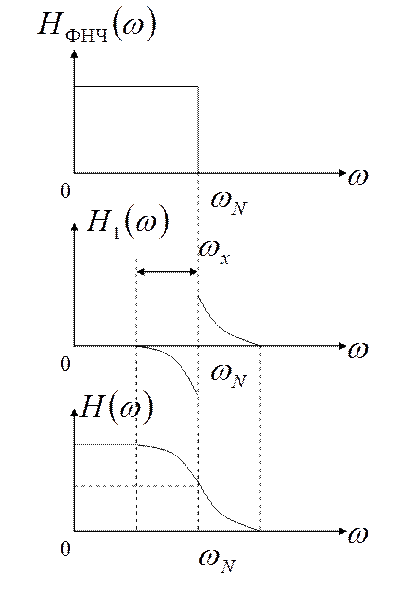
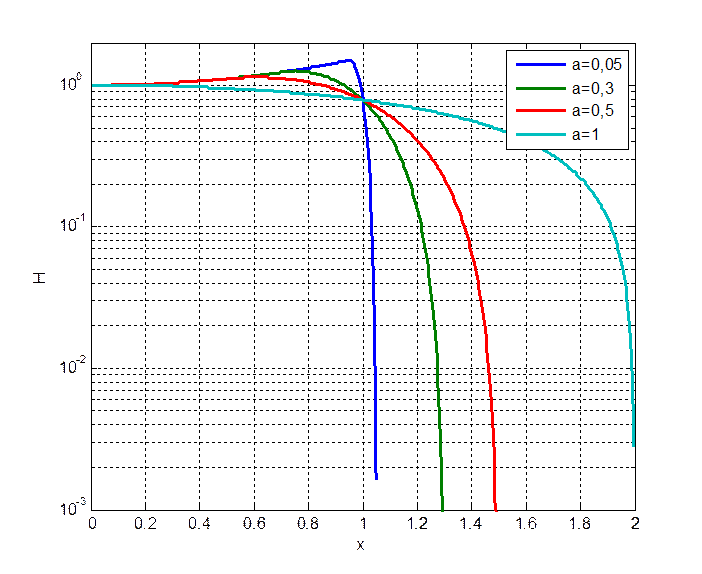
АЧХ фильтра вида «приподнятый косинус»:
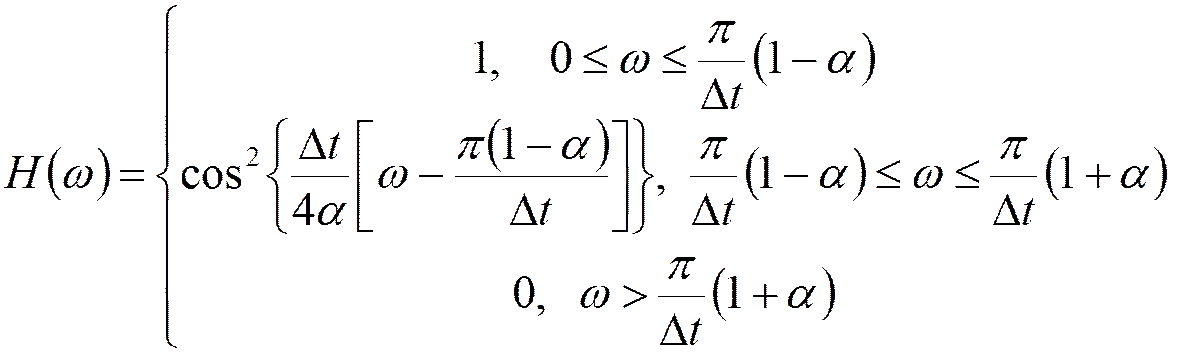
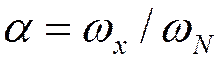 - коэффициент скругления
- коэффициент скругления
Это обеспечивает отсутствие межсимвольных искажений
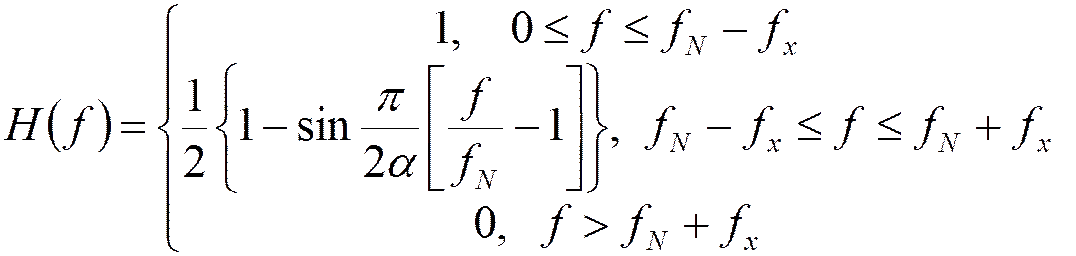
С учетом АЧХ амплитудного корректора:
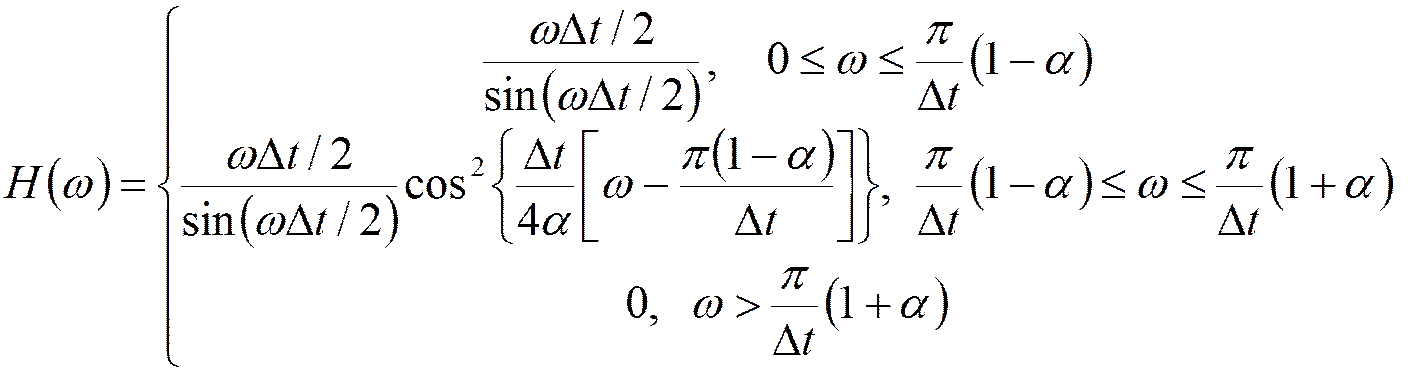
![]() - фильтр нереализуемый
- фильтр нереализуемый
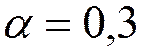 - джиттер 36%
- джиттер 36%
![]() - джиттер 0%, полоса частот в 2 раза
больше минимальной
- джиттер 0%, полоса частот в 2 раза
больше минимальной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.