Анализ надёжности артиллерийского орудия при помощи программного обеспечения OBRIS

Балтийский Государственный Технический Университет им. Д.Ф.Устинова «Военмех»

_________________________________________________

Кафедра Е1

Анализ надёжности артиллерийского орудия

при помощи программного обеспечения OBRIS

Преподаватель: Вященко Ю.Л.

Студент: Шибко А.В.

Группа: Е112 

                            Зач.кн. № Е11317

Санкт-Петербург

2005

 Содержание

Описание пакета прикладных программ OBRIS используемых для определения вероятности безотказной работы, определяемой по результатам испытаний.

Оценка показателя надежности (в данном случае вероятности безотказной работы) производится при помощи пакета прикладных программ OBRIS по результатам испытаний (в данном случае условных). Пакет использует модели испытаний, оперирующие данными ти­па: «успех - отказ - доработка».

Задача определения оценки вероятности безотказной работы по результатам испытаний разбита на ряд подзадач:

ü  подзадача принятия решения об однородности исходной информации;

ü  подзадача выбора модели испытаний;

ü  подзадача определения оценок параметров модели испытаний;

ü  подзадача определения оценок показателей надежности по модели ис­пытаний.

Ограничения на применение для программных средств, решающих за­дачу определения оценки показателя надежности КЧ по результатам испытаний, следующие:

ü  число серий испытаний NIS < 30;

ü  при числе серий испытаний более 3-х КЧ должна иметь устойчивую тенденцию к не уменьшению безотказности к концу испытаний;

ü  в каждой серии испытаний число испытаний должно превышать число отказов: ;

ü числа испытаний в различных сериях испытаний не должны отличаться более чем на порядок:

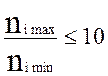
ü числа устранённых причин отказов в различных доработках не должны отличаться более чем в три-пять раз: .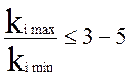

Подзадача принятия решения об однородности исходной информации. Решение подзадачи заключается в нахождении нижних и верхних до­верительных границ вероятности безотказной работы в каждой серии испы­таний и проверке биномиальной гипотезы для каждой серии. При этом за фиксируемый уровень принимается точечная оценка вероятности безотказ­ной работы, определённая по схеме Бернулли по суммарной наработке всех серий испытаний.

Определение доверительных границ вероятности безотказной работы основано на решении уравнений Клеппера-Пирсона с использованием ап­проксимации неполной бета-функцией (Судаков Р.С. и др. Статистические задачи отработки систем и таблицы для числовых расчётов показателей на­дёжности. М., Высшая школа, 1975 г.).

Подзадача выбора модели испытаний артиллерийской системы

Выбор модели испытаний регламентирован характером исходных дан­ных.

При однородных данных или при единственной серии испытаний при­нимается биномиальная модель (ГОСТ В20.57.304-76).

При неоднородных данных и не более трёх серий испытаний принима­ется рекуррентная модель (Тёскин О.И - Оценка надёжности систем на этапе экспериментальной отработки. Сборник: Обработка результатов испытаний на надёжность. М., Знание, 1981 г.).

При неоднородных данных и более трёх серий испытаний принимается аппроксимационная модель (Волков Л.И., Шишкевич А.М. Надёжность лета­тельных аппаратов. М., Высшая школа, 1975 г.).

Подзадача определения оценок параметров моделей испытаний.

Определение оценки параметра  рекуррентной моделиW_i

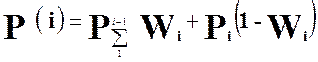
основано на использовании «точного критерия Фишера» (матрицы 2х2).

  Определение оценок параметров , , aаппроксимационной модели

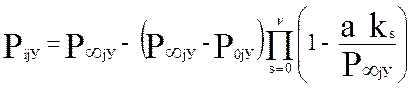
основано на поиске максимума функции максимального правдоподобия.

Подзадача определения оценок показателей надежности по модели испытаний.

Принятая модель испытаний реализуется при вычисленных оценках параметров. В результате определяются точечная оценка вероятности безотказной работы, точечная оценка средней наработки на отказ, нижняя доверительная граница вероятности безотказной работы, нижняя доверительная граница средней наработки на отказ, эквивалентное число отказов и, при рекуррентной модели, эквивалентное число испытаний.

Входные и выходные данные пакета прикладных программ.

Входными данными задачи определения вероятности безотказной работы артиллерийской системы являются:

ü  число серии испытании;

ü  количество испытаний в каждой серии;

ü  количество отказов в каждой серии;

ü  количество причин отказов, устранённых в каждой доработке.

Выходными данными задачи определения вероятности безотказной работы артиллерийской системы являются:

ü  точечная оценка вероятности безотказной работы;

ü  точечная оценка средней наработки на отказ;

ü  нижняя доверительная граница вероятности безотказной работы при доверительной вероятности 0,8;

ü  нижняя доверительная граница средней наработки да отказ при доверительной вероятности 0,8;

ü  эквивалентное число отказов;

ü  эквивалентное или фактическое число испытаний.

Анализ при помощи БИНОМИНАЛЬНОЙ МОДЕЛИ.

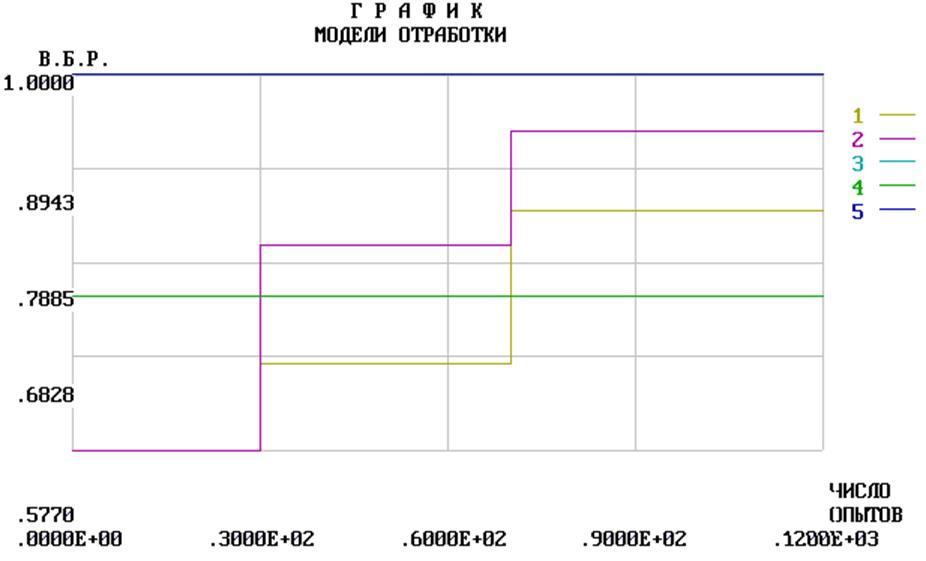
Анализ при помощи РЕКУРЕНТНОЙ МОДЕЛИ.

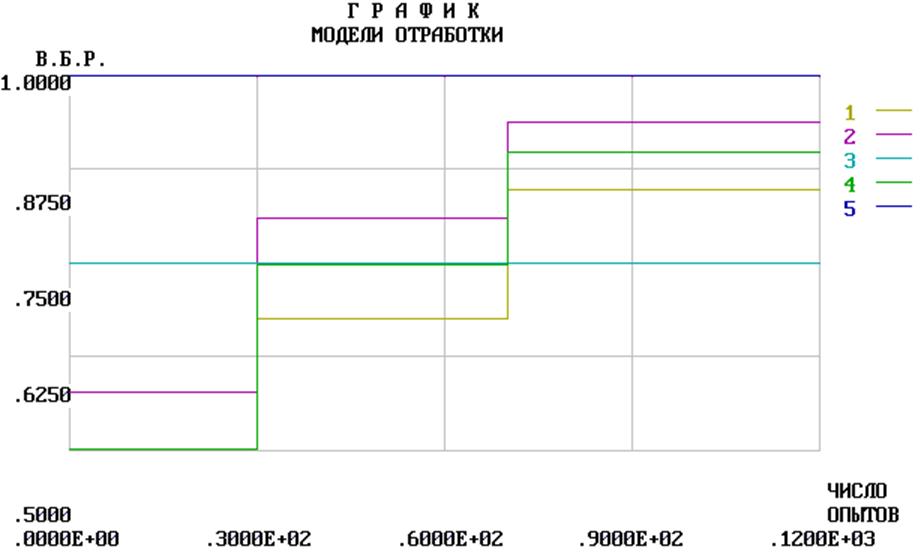
Анализ при помощи АПРОКСИМИРУЮЩЕЙ МОДЕЛИ.

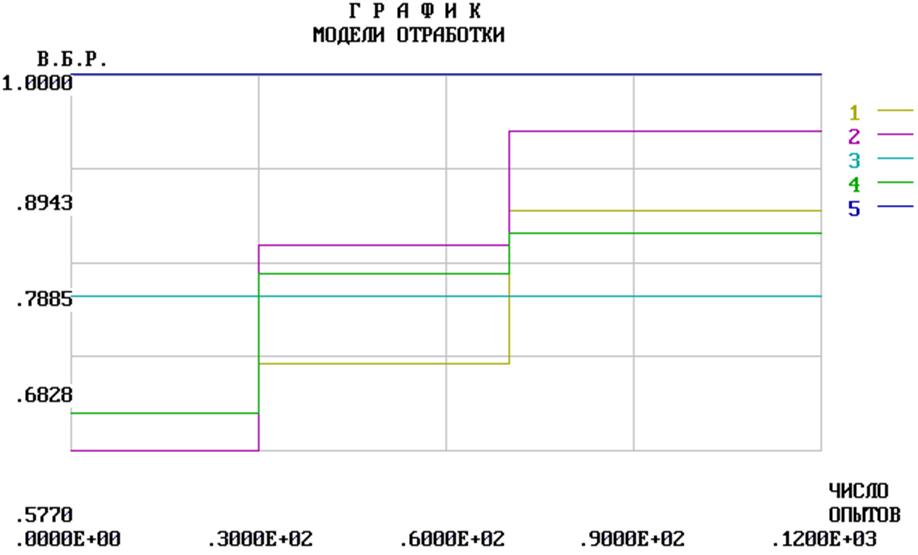
Анализ по всем моделям.

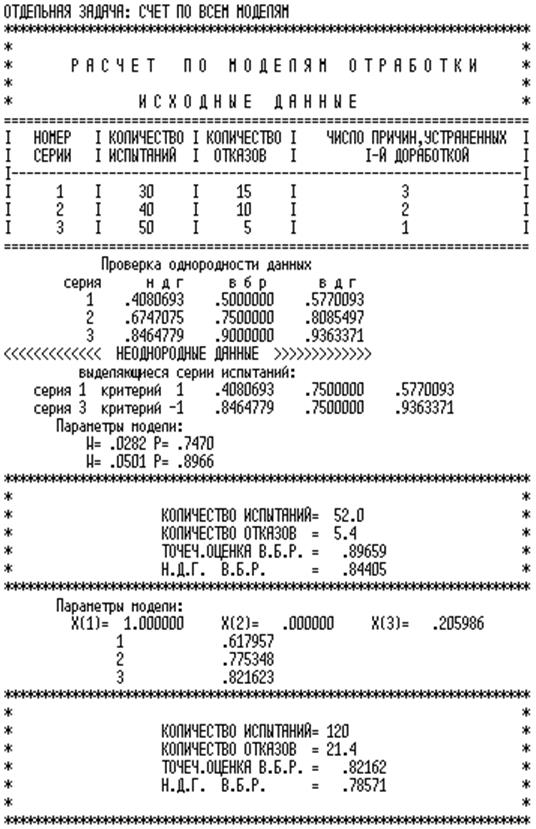
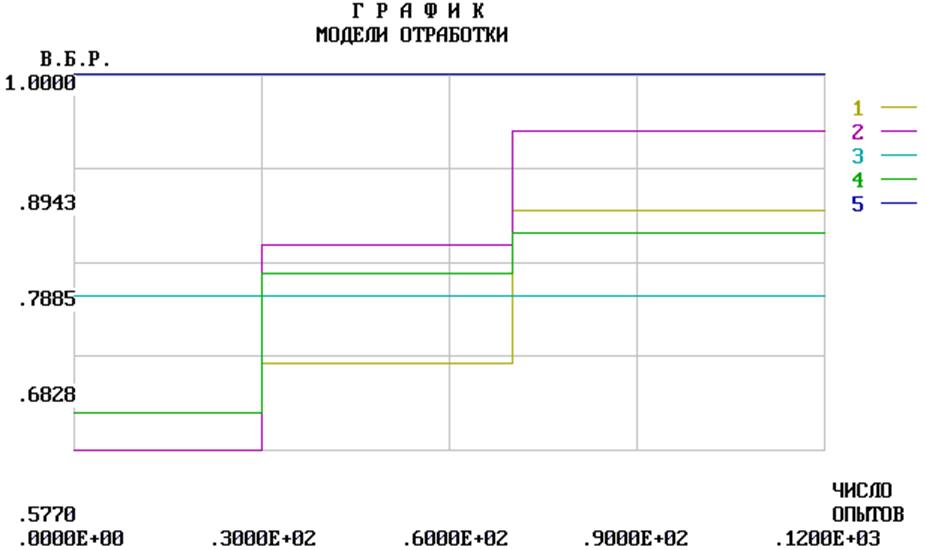
Выводы

В данной работе был произведён анализ данных, полученных в результате испытаний артиллерийского орудия.

Анализ экспериментальных данных при помощи биноминальной схемы выявил их неоднородность.

Следовательно, анализировать данные следует по аппроксимирующей и рекуррентной моделям.

Анализ данных с помощью рекуррентной модели дал наилучшие, по сравнению с аппроксимирующей моделью, результаты. Это подтверждает правило, что рекуррентная модель работает лучше в тех случаях, когда количество серий испытаний не превышает трёх. В случае, когда количество серий испытаний превышает три, следует пользоваться аппроксимирующей моделью.