Квантование радиосигналов (Лабораторная работа № 1)

Федеральное агентство по образованию РФ

РГРТУ

Кафедра РТУ

Лабораторная работа № 1

"Квантование радиосигналов"

Выполнил:

Студент 815 группы

Тараскин А.С.

Хонякин И.Н.

Кочетков А.Н.

Калинчева К.О.

Проверил:

Гусев С.И.

Рязань 2012

Цель работы: исследование шумов и помех, возникающих в АЦП вследствие нелинейности, а также наличия источников теплового шума.

Экспериментальная часть.

1. Определение уровня шума квантования

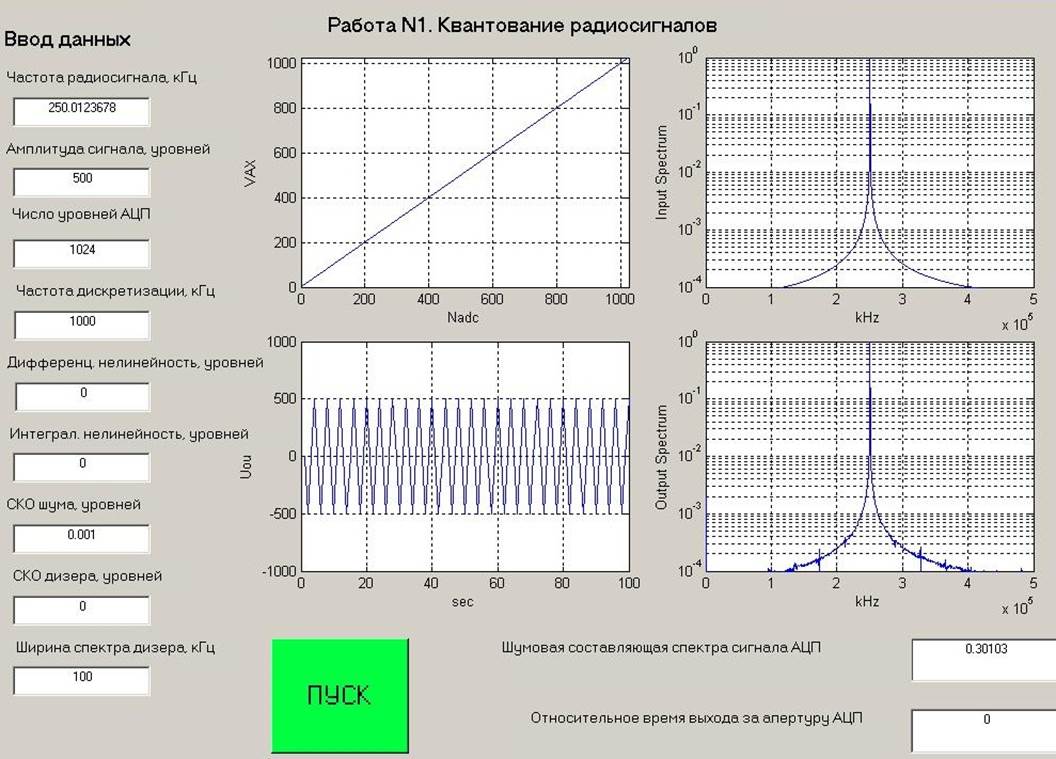
          В качестве экспериментальных данных выставлено: N_АЦП=1024 уровня,

f_д=1000кГц,f₀=250кГц,f_диз=100кГц, ∆h_диф=0, ∆h_инт=0, σ_диз=0, A_m=500 уровней, σ_ш=10^-3.

          В результате ненормированное среднеквадратичное значение  шумовой составляющей спектра выходного сигнала АЦП, рассчитанное в полосе частот, где сигнала отсутствует.

2. Снятие зависимости отношения сигнал/шум от амплитуды входного сигнала АЦП

          Пронаблюдать и зарисовать форму спектра выходного сигнала АЦП.

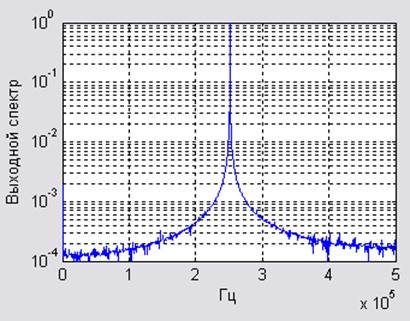Т.о АЦП изменяет спектр выходного сигнала, что является признаком наличия шумов квантования, связанных с округлением или усечением аналогового сигнала.

Определить уровень сигнала на выходе АЦП по амплитуде гармонической составляющей спектра на частоте сигнала. Рассчитать отношение сигнал-шум

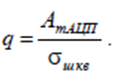
         Повторить эксперимент для нескольких значений амплитуды входного сигнала, при которых заметно изменение отношения сигнал-шум. Построить график зависимости :

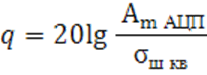
	100	200	300	400	500
	1	1	1	1	1
	0.29261	0.28619	0.29236	0.3045	0.28372
q, дБ	10.839	10.577	10.934	9.947	10.730

        

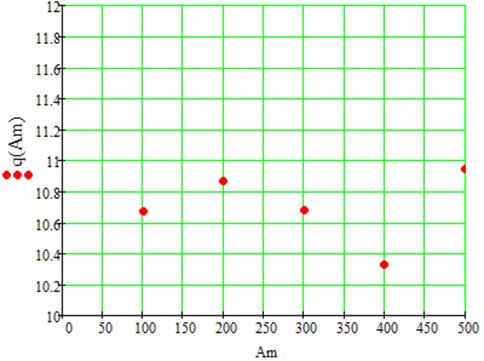
         Таким образом, не имеет смысла сильно увеличивать амплитуду сигнала на входе АЦП, что приводит к выходу сигнала за апертуру АЦП и уменьшению отношения сигнала/шума.

4.3 Исследование влияния дифференциальной нелинейности на уровень шума

          Введение дифференциальной нелинейности в АЦП приводит к изменению передаточной характеристики АЦП, что характеризуется случайным изменением шага квантования h.

          В качестве экспериментальных данных выставлено: N_АЦП=1024 уровня,

f_д=1000кГц,f₀=250кГц,f_диз=100кГц, ∆h_диф=0.5, ∆h_инт=0, σ_диз=0, A_m=500 уровней, σ_ш=10^-3

	0	0.5	1	10	100
	0.29072	0.40245	0.40218	0.39785	0.39951

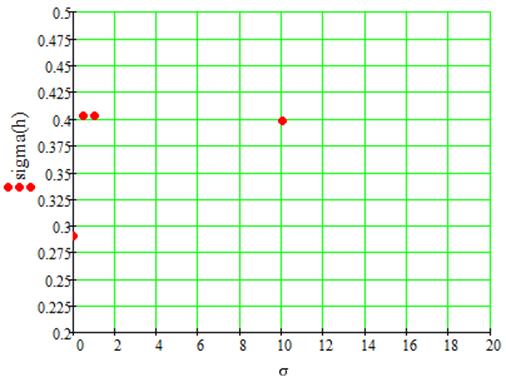
          Введение дифференциальной нелинейности приводит к увеличению шумовых составляющих выходного спектра. Это связано с изменением равномерного закона шага квантования на другой случайный закон, вследствие чего увеличивается общая дисперсия шума квантования.

4.4 Исследование влияния интегральной нелинейности на уровень шума

          Интегральная нелинейность эквивалентна изменению среднего значения передаточной характеристик АЦП. В результате она отличается от равномерной.

          В качестве экспериментальных данных выставлено:  N_АЦП=1024 уровня,

f_д=1000кГц,f₀=270кГц,f_диз=20кГц, ∆h_диф=0, ∆h_инт=10 ур., σ_диз=0, A_m=500 уровней, σ_ш=30

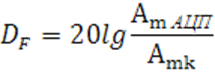
	50	60	70	80	90	100
	1	1	1	1	1	1
	0.09	0.085	0.075	0.075	0.06	0.05
	20.915	21.412	22.498	22.498	24.237	26.021

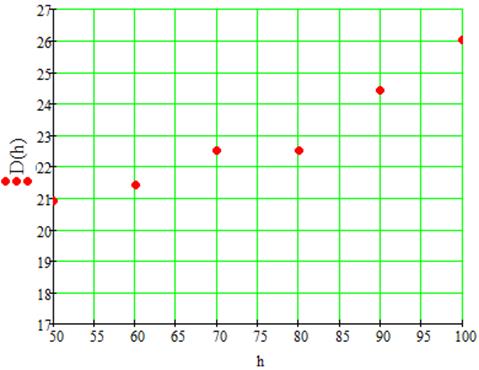         Введение интегральной нелинейности приводит к изменению спектра выходного сигнала – появляются новые спектральные составляющие с частотами, кратными частоте сигнала. Т.о. появляются нелинейные искажения сигнала подобно аналоговой техники. Увеличение интегральной нелинейности соответственно понижает свободный от шумов динамический диапазон сигнала. Это снижает возможный уровень сигнала на входе АЦП.

4.5 Исследование влияния широкополосного дизера на свободный динамический диапазон (в качестве дизера – тепловой шум)

          В качестве экспериментальных данных выставлено:  N_АЦП=1024 уровня,

f_д=1000кГц,f₀=270кГц,f_диз=20кГц, ∆h_диф=0, ∆h_инт=10, σ_диз=0, A_m=200 уровней, σ_ш=10^-3

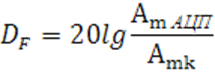
	10	20	30	40	50
	1	1	1	1	1
	0.09	0.085	0.095	0.1	0.005
	13.979	14.895	18.416	26.021	27.959

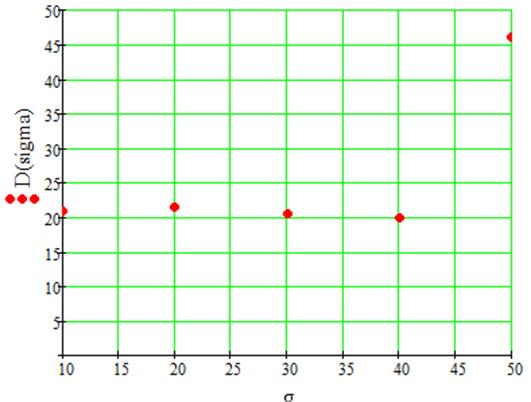
          Введение дизера (случайного шума как модели широкополосного теплового шума) во входной сигнал приводит к увеличению динамического диапазона при тех же значениях интегральной нелинейности. Это связано с усреднением значений передаточной характеристики АЦП, что приводит к выравниванию шага квантования. В результате интегральная нелинейность снижается и увеличивается свободный динамический диапазон.   

4.6 Исследование влияния узкополосного дизера на свободный динамический диапазон

          Вторым способом является использование не широкополосного, а узкополосного дизера, сосредоточенного вблизи частоты сигнала. Это позволяет снизить дополнительно вводимые шумы вне полосы сигнала.

          В качестве экспериментальных данных выставлено:  N_АЦП=1024 уровня,

f_д=1000кГц,f₀=270кГц,f_диз=20кГц, ∆h_диф=0, ∆h_инт=10, σ_диз=0, A_m=200 уровней, σ_ш=10^-3

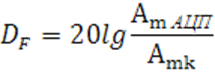
	50	60	70	80	90	100	120
	1	1	1	1	1	1	1
	0.08	0.08	0.09	0.1	0.1	0.14	0.2
	21.938	21.938	20.915	20	20	17.077	13.979

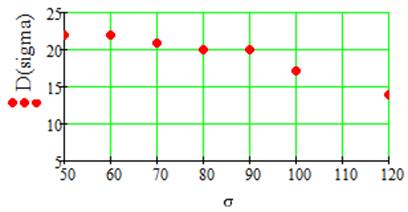
Вывод:

          В данной работе были исследованы процессы, происходящие в АЦП при обработке сигнала. Фундаментальными причинами искажения сигнала являются наличие шумов квантования (даже в идеальном в теоретическом смысле АЦП), дифференциальной и интегральной нелинейностей. Одним из способов уменьшения нелинейности является «подкрашивание» сигнала шумом (либо внеполосный, либо широкополосным). Это усредняет шаг квантования и увеличивает свободный динамический диапазон и отношение сигнал-шум. Еще одним способом увеличения сигнал-шум является существенное увеличение частоты дискретизации – передискретизация. Так как мощность шумов при  этом остается той же, а спектральная плотность шумов распределяется по большей полосе частот, определяемой частотой дискретизации. Это ведет к увеличению ДД.