Функционально-стоимостной анализ: Методические указания к практическим занятиям, страница 8

7.1. Расчет показателя обобщенного качества.

Дальнейший отбор вариантов исполнения основных (главной) функций осуществляется на основании оценки качества вариантов в соответствии с выбранными критериями качества.

Для такой оценки используются экспертные методы (бальный, оценки по приоритетам и т.д.).

В целях повышения достоверности результатов будем использовать метод расстановки приоритетов (оценки по приоритетам), который включает следующие этапы :

1.  Согласно “дереву целей” выбирают критерии (показатели, параметры), по которым будем анализировать варианты и обозначают их:

k₁,k₂,…,k_i,… - критерии качества;

x₁,x₂,…,x_i,… - варианты реализации изделия.

2.  Составляют матрицу смежности критериев для определения абсолютных (B_i) и относительных (b_i) значимостей, причем bi определяется как

                                                (7.1)

3.  Для каждого критерия аналогичным способом определяют абсолютные (P_ij) и относительные (p_ij) приоритеты вариантов реализации объекта.

4.  Рассчитывают показатель обобщенного качества (Q_i) для каждого варианта по формуле

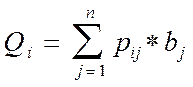,                                              (7.2)

где p_ij – относительный приоритет i-го варианта  исполнения  РЭА  по  j-му критерию;

bj – относительная значимость j-го критерия.

Об оптимальности варианта можно судить по максимальности показателя обобщенного качества.

ПРИМЕР: Представим, что отбор лучшего из предложенных изделий (X1, X2, X3 - варианты исполнения), согласно “дереву целей”, целесообразно проводить по следующим  3 - м критериям:

1. Габаритные размеры - K1.

2. Масса - K2.

3. Эргономичность  - K3.

В целях повышения достоверности экспертных оценок при сравнении вариантов , и систематизации процедур экспертизы  лучше использовать метод расстановки приоритетов.

На первом этапе составим матрицы смежности для сравнения вариантов функции F1 по каждому из критериев.

a)ПО КРИТЕРИЮ ГАБАРИТНЫХ РАЗМЕРОВ (K1):

	X1	X2	XЗ	Сумм	Pi1	рi1
X1	= 1	<  0.5	<  0.5	2.0	5.5	0.22
X2	> 1.5	=  1	<  0.5	3.0	8	0.32
XЗ	>   1.5	>  1.5	= 1	4.0	11.5	0.46
Сумма				9.0	25	1

Абсолютные приоритеты вариантов функции :

Для расчета Рv(1) каждая строка в матрице умножается на вектор - столбец (Сумм.).

Р_1.1 = 1*2.0+0.5*З.0+0.5*4.0=5.5

Р_2.1 = 1.5*2.0+1*3.0+0.5*4.0=8

Р_3.1 = 1.5*2.0+1.5*3.0+1*4.0=11.5

Относительные приоритеты :

р_1.1 = 5.5/25=0.22

р_2.1 = 8/25=0.32

р_3.1 = 11.5/25=0.46

б)ПО КРИТЕРИЮ МАССЫ (K2)

	X1	X2	XЗ	Сумм	Рi2	pi2
X1	= 1	>  1.5	> 1.5	4.0	11.5	0.46
X2	< 0.5	= 1	>  1.5	3.0	8	0.32
XЗ	< 0.5	<  0.5	= 1	2.0	5.5	0.22
Сумма				9.0	25	1.0

Абсолютные приоритеты :

Р_1.2 = 1*4.0+1.5*3.0+1.5*2.0=11.5

P_2.2 = 0.5*4.0+1*З.0+1.5*2.0=6

Р_3.2 = 0.5*4.0+0.5*3.0+1**2.0-5.5

Относительные приоритеты :

p_1.2 = 11.5/25=0.46

p_2.2 = 8/25=0.32

p_3.2 = 5.5/25=0.22

в) ПО КРИТЕРИЮ ЭРГОНОМИЧНОСТИ(K3).

	X1	X2	XЗ	Сумм	Рi3	pi3
X1	= 1	<  0.5	<  0.5	2.0	9.25	0.22
X2	>  1.5	= 1	>  1.5	4.0	21.25	0.46
XЗ	>  1.5	<  0.5	= 1	3.0	12.25	0.32
Сумма				9.0	25	1.0