Статический расчёт системы стабилизации скорости ЭП типа ТВ-Г-Д, страница 2

-LG(LM)-обмотка возбуждения генератора (двигателя)-формирует поток возбуждения генератора(двигателя).

-ВА-датчик тока якорной цепи.

-LM-обмотка возбуждения двигателя.

5) Расчет параметров генератора как обобщенного преобразователя

Режим работы ЭП на номинальной скорости:   

Эквивалентное сопротивление якорной цепи генератора и двигателя:

 

 ЭДС двигателя в номинальном режиме:

                            

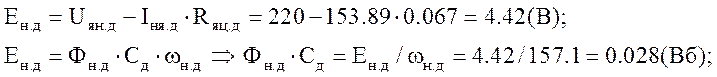
ЭДС генератора, соответствующая номинальному режиму работы привода:

 

  

Номинальный (паспортный) ток возбуждения генератора:

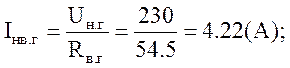
Номинальный (паспортный) магнитный поток генератора определяем по характеристики намагничивания (рис.1):

Номинальная ЭДС генератора(паспортная):

Конструктивная постоянная генератора:

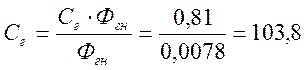
Магнитный поток генератора соответствующий номинальному режиму:

 

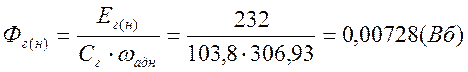
Ток возбуждения генератора, необходимый для работы ЭП в номинальном режиме определяем по характеристики намагничивания:

Коэффициент передачи генератора для номинального режима:

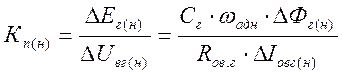
и  находим по рис.2

;

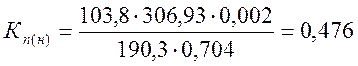
Индуктивность обмотки возбуждения соответствующая номинальному режиму:

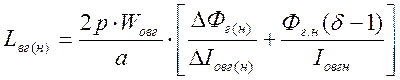,где

-число пар полюсов генератора

-число параллельных ветвей.   

-коэффициент рассеяния обмотки возбуждения   

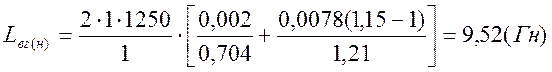
Постоянная времени обмотки возбуждения для номинального режима:

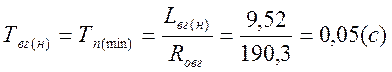
6) Режим работы ЭП на минимальной скорости .

Минимальная скорость двигателя:

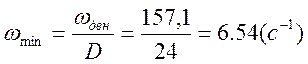
где, D – заданный диапазон регулирования

ЭДС генератора, обеспечивающая :

Магнитный поток генератора соответствующий :

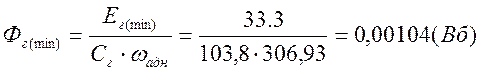
Ток возбуждения генератора необходимый для работы ЭП на минимальной скорости:

Определяем по характеристике намагничивания:

Напряжение обмотки возбуждения генератора при :

Коэффициент передачи генератора для режима, обеспечивающего :

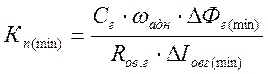
так как участок кривой намагничивания при и  линейный, то можно принять

  ;

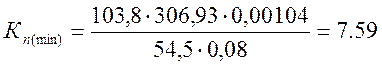
Индуктивность обмотки возбуждения при :

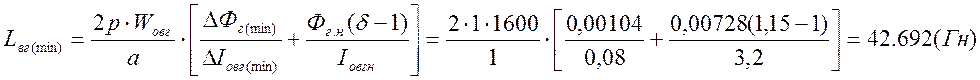
Постоянная времени обмотки возбуждения при :

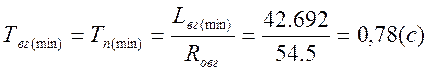
7)Расчет параметров структурной схемы привода.

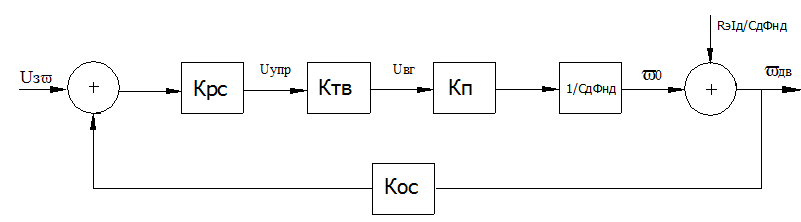
Рис.3 Структурная схема СУЭП в установившемся режиме.

Принимаем

Коэффициент обратной связи по скорости:

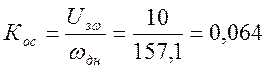
Максимальное напряжение обмотки возбуждения генератора:

, где -коэффициент форсировки возбуждения.

 Берем

Коэффициент усиления тиристорного возбудителя:

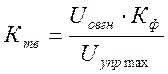, где -максимальное напряжение управления тиристорным возбудителем.

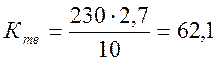
Для нахождения коэффициента передачи регулятора скорости по рис.4 запишем уровнение скоростной характеристики электропривода:

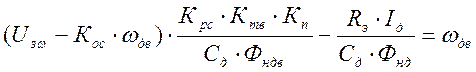 (3)

Из (3) выражаем  и получаем уравнение скоростной характеристики ЭП.

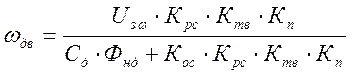
Чтобы определить  учитываем требования к статической точности регулирования. Ошибка максимальная при минимальной частоте вращения:

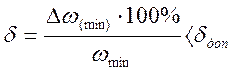=2%

Выражаем

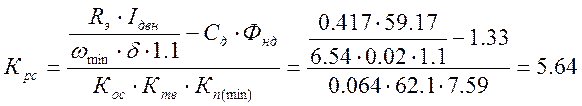
Статическая просадка скорости при работе на характеристике, обеспечивающей  при номинальном токе двигателя:

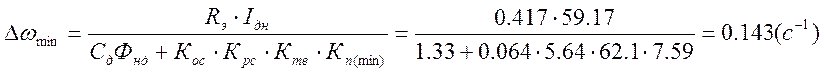
Скорость идеального холостого хода:

Уровень задающего напряжения, обеспечивающий :

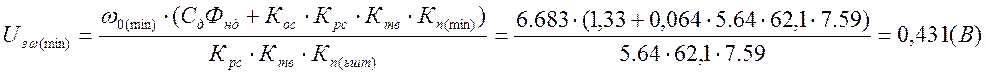Рассчитываем уровень задающего напряжения, обеспечивающего номинальный режим работы привода.

Статическая просадка скорости:

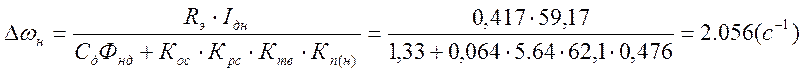
Скорость идеального холостого хода:

 

Уровень задающего напряжения, обеспечивающий номинальный режим работы привода:

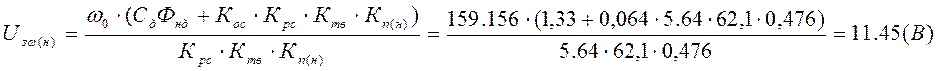
8) Расчет токовой отсечки.

Статическая структурная схема СУЭП для расчета параметров узла токовой отсечки.

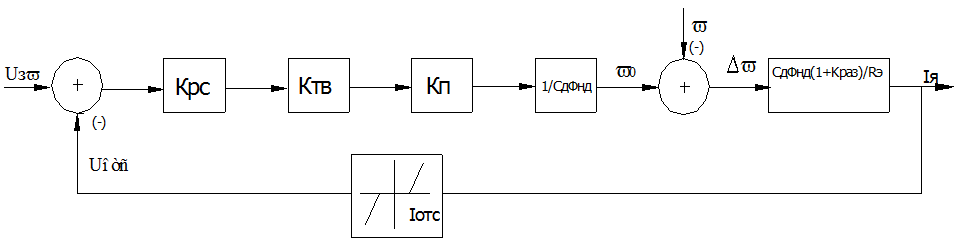
     Рис.4 Статическая структурная схема СУЭП для расчета токовой отсечки.

Токовая отсечка рассчитывается при максимальном сигнале задания скорости

Ток отсечки:

 

Ток упора:

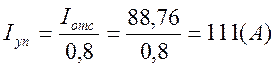
Коэффициент усиления разомкнутой СУЭП:

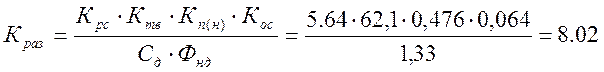
Напряжение обратной связи по току на участке токовой отсечки:

  (4)

По рис. 4 запишем выражение для тока якоря:

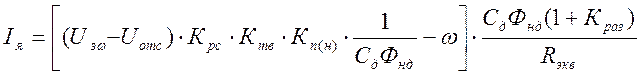   (5)

Из (5) выражаем  при   

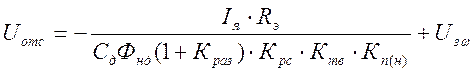 (6)

при

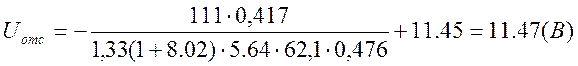
Из (4) выражаем

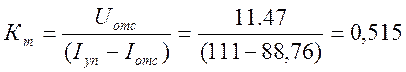
Участок отсечки на характеристике для номинальной скорости:

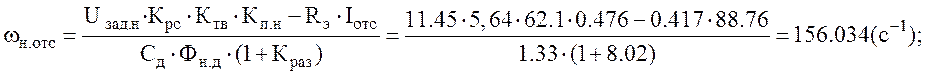
Жесткость характеристики токовой отсечки:

   

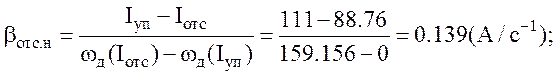
Участок отсечки на характеристике для минимальной скорости:

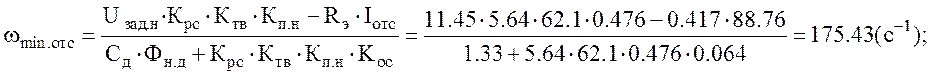Жесткость характеристики токовой отсечки:

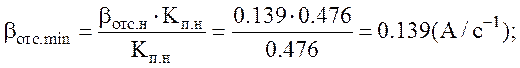
Статическая просадка при отсечки на номинальной скорости:

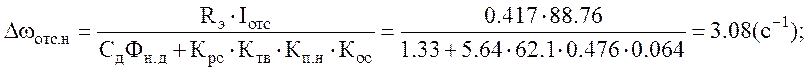
9) Построение скоростных характеристик ЭП.

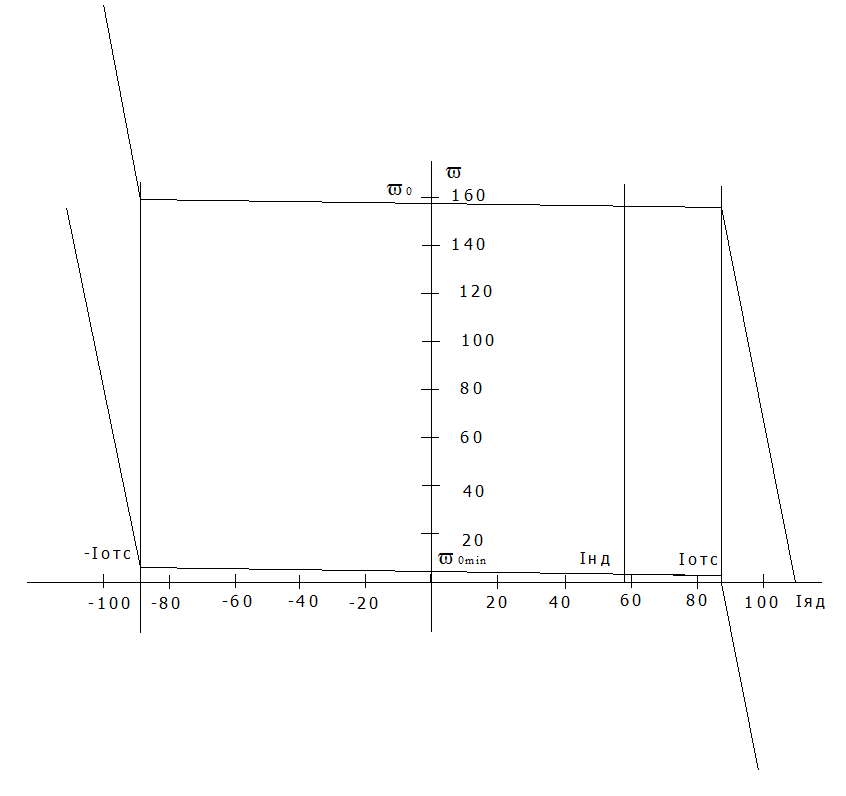                                             Рис.5 Скоростные характеристики электропривода.

10) Анализ устойчивости синтезированной системы электропривода.

Наиболее неблагоприятные условия для устойчивости создаются при работе на номинальной скорости вращения.

Составляем структурную схему с учетом инерционности преобразователя и двигателя. 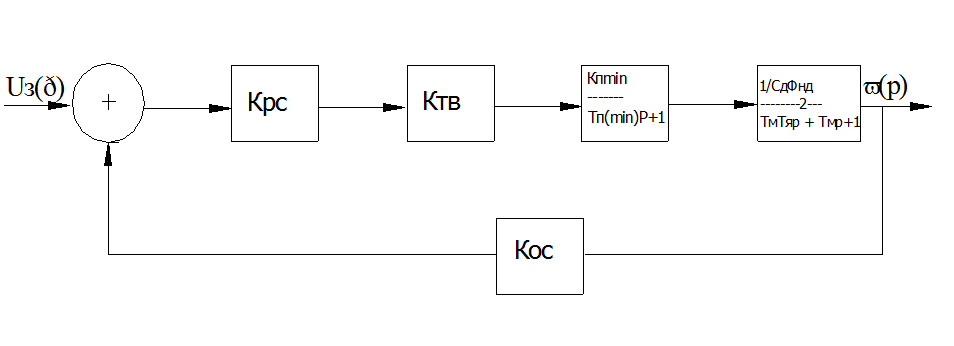                      Рис.6 Структурная схема СУЭП для рабочих нагрузок.

На рис.6 обозначено.

Электромеханическая постоянная времени привода:

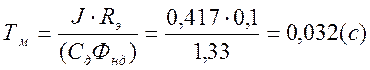
Электромагнитная постоянная времени якорной цепи:

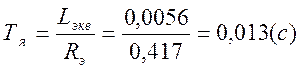
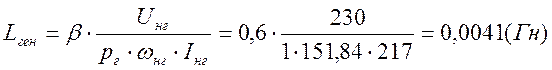
где -коэффициент компенсации

По рис.7 записываем выражение для передаточной функции замкнутой системы:

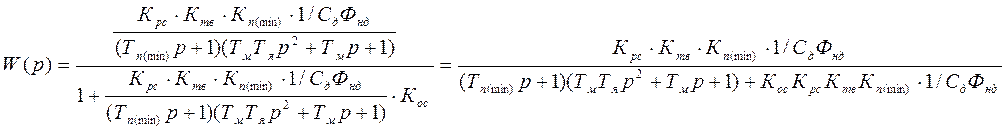Характеристический полином замкнутой системы имеет вид:

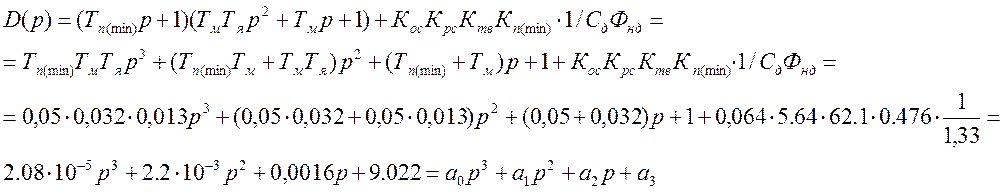Для исследования устойчивости воспользуемся алгебраическим критерием Гурвица:

 Для устойчивости замкнутой системы необходимо и достаточно, чтобы n диагональных миноров матрицы Гурвица были положительны, где n-степень характеристического полинома замкнутой системы.

Составляем матрицу Гурвица:

 

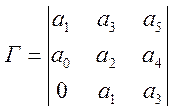
Синтезированная система электропривода неустойчивая.

Для обеспечения устойчивости системы необходимо синтезировать корректирующие устройства, либо изменить требования, предъявляемые к качеству системы: уменьшить диапазон регулирования скорости, либо увеличить ошибку в установившемся режиме. Так же систему можно сделать устойчивой, увеличив механическую постоянную времени, но это приведет к снижению быстродействия.

Министерство образования и науки Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра электропривода и автоматизации промышленных установок

«Статический расчёт системы стабилизации скорости ЭП

типа ТВ-Г-Д»

Вариант №14

Факультет: ЭМ

Группа: Эм-31               

Студент: Кожемяков А.А.

Преподаватель: Панкратов В.В.                                                         

Новосибирск 2007г.