Расчет асинхронного электродвигателя типа 4MTF(H)-160LB8, страница 2

S	---	-0,5	-0,2	-0,08	0	0,08	0,2	0,5	0,8	1	1,2	1,5	1,8	2
ω	с-1	117,8	94,2	84,8	78,5	72,2	62,8	39,3	15,7	0	-15,7	-39,3	-62,8	-78,5
M	Н·м	-206,7	-468,1	-692,8	0	611,4	429,5	198,8	127,1	102,3	85,5	68,6	57,3	51,6
sin ψ2	---	0,995	0,949	0,733	0	0,689	0,909	0,976	0,987	0,990	0,992	0,993	0,994	0,995
I1	А	118,71	113,48	89,68	29,60	84,86	109,07	116,59	117,79	118,12	118,31	118,49	118,59	118,64
I2’	А	89,21	85,01	65,69	0	61,71	81,46	87,51	88,48	88,74	88,89	89,03	89,12	89,16

             Механическая характеристика представлена на (Рис.3.), скоростные характеристики представлены на (Рис.4.).

Из (Рис3.) определяем  при спуске и подъёме груза, для вычисления линейных скоростей подъёма и спуске груза.

Скорость подъёма: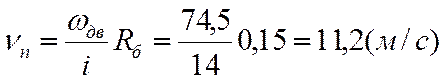   

Скорость спуска: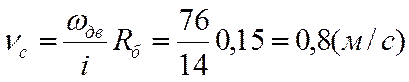

4.  Построить пусковую диаграмму электродвигателя при питании его от сети с неизменным напряжением, равное половинному. Определить величину сопротивления пусковых ступеней п. Определим сопротивления  графическим методом.

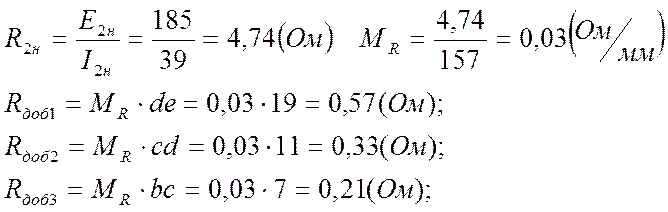
Характеристики представлены на (Рис5).

5.  Определить сопротивление и построить искусственную реостатную механическую характеристику электродвигателя, обеспечивающую в режиме противовключения при спуске груза скорость вращения равную .

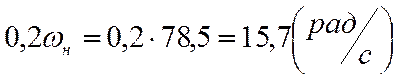
Сопротивление вычисляем по следующей формуле:

               

 

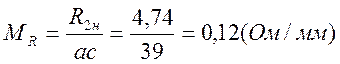
Характеристика представлена на (Рис 6).

6.  Определить скорость опускания груза, если электродвигатель будет работать на характеристике пункта «5» но в режиме генераторного торможения с рекуперацией энергии в сеть. Характеристика приведена на (Рис.6). По рисунку определим что 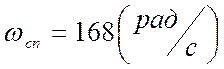, вычисляем скорость.

  

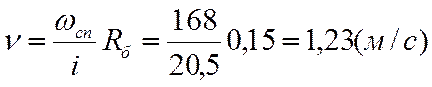
7.  Определить сопротивление и построить механическую характеристику динамического торможения, обеспечивающую при начальной скорости торможения, равной установившейся скорости подъёма.

Для асинхронного электродвигателя значение заданного начального момента приравнивается величине критического момента при динамическом торможении, а соответствующее ему критическое скольжение определяется заданной начальной скоростью торможения.  

Задаёмся значениями  и  находим величину фазного эквивалентного тока .

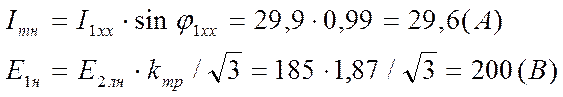
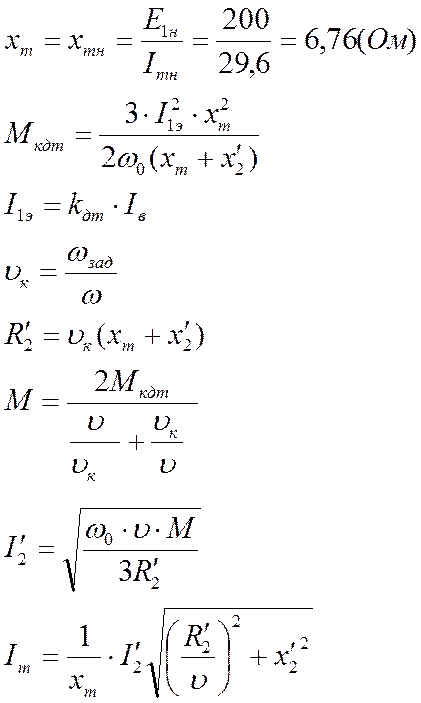
– коэффициент эквивалентности тока  току  (при подаче тока в две линии статора, обмотки которого соединены звездой ).

             Предварительно задаемся значениями:

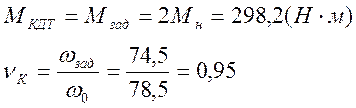
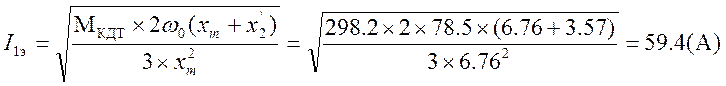
Остальные рассчитанные данные занесены в таблицу 2.

Таблица 2

S	---	0	0,25	0,5	0,75	0,95	1	1,25	1,5
ω	c-1	0	19,6	39,3	58,9	74,6	78,5	98,1	117,8
M	Н·м	0	146,78	245,80	290,06	298,20	297,81	287,31	269,59
Im	А	0	9,24	13,73	16,63	18,13	18,42	19,52	20,19
I2’	А	0	9,90	18,12	24,10	27,50	28,20	30,97	32,86

Характеристика представлена на (Рис.7.). Находим сопротивление:

(Ом)

Задача №2.

1.  Рассчитать и построить графики механических переходных процессов  электропривода грузоподъёмной лебёдки в следующих режимах:

При реостатном пуске в режиме подъёма груза.

Принимаем допущение о линейности механических (естественных и искусственных) характеристик на всём допустимом диапазоне изменении их статически и динамических нагрузок. В этом случае решение уравнения движения электропривода в одномассовой жёсткой системе 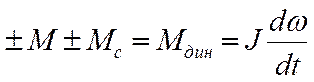 имеет вид:

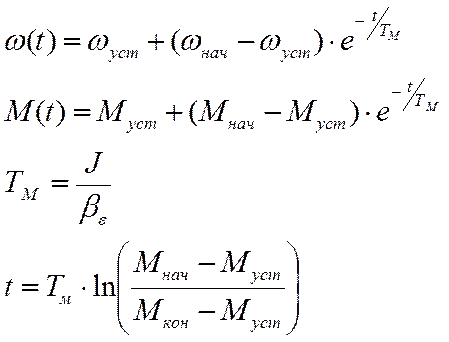
 – начальное значение угловой скорости и  момента двигателя.

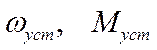  – установившееся значение угловой скорости и вращающегося момента двигателя по окончанию переходного процесса.

 – время.

 – электромеханическая постоянная времени.

 – суммарный момент жёсткости механической характеристики двигателя и механизма, при  тогда .

Результаты расчетов ,, сведены в таблицу 3:

Таблица 3

β	----	6,35	10,81	17,39	28,57
ТМ	c	0,091	0,054	0,033	0,02
t	c	0,069	0,041	0,025	0,015