Рис. 4.11. Поток рассеяния в зубцах /, поток рассеяния в лобовых частях 2, 3 - шихтованный стальной сердечник, 4 - катушка, 5 ~ проводник
|
|
Рис. 4.12. Основной поток Фm и поток рассеяния ![]() контура
контура
Вопрос 33.
Графический метод определения магнитодвижущих сил.
Рис. 4.19. Схема распределенной обмотки статора {q= 3) двухполюсной
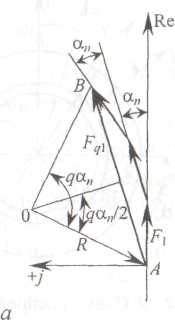
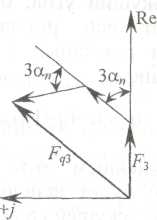
Рис. 4.20. К определению МДС группы катушек: а - основных гармоник, б - третьих гармоник
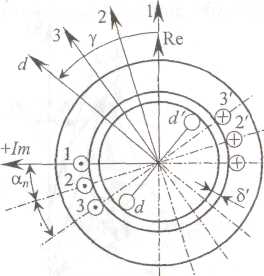
Здесь полезно привести и другой путь получения МДС распределенной обмотки, основанный на представлении синусоидальной величины в виде вектора. Совместим начало координат с осью вращения, а вещественную ось - с
осью МДС катушки 1-1. Напомним, что ось МДС катушки направлена перпендикулярно к плоскости, на которой лежат ее активные стороны. Положительное направление оси совпадает с направлением магнитного потока, созданного током катушки, принятым за положительное направление в контуре.
![]()
![]() На рис. 4.19 показано взаимное положение
векторов, соответствующих основным гармоническим МДС катушек. Они сдвинуты в пространстве на угол. Их сумма дает
результирующее значение .Из построения на рис. 4.20, а нетрудно
получить выражение для первой гармоники
На рис. 4.19 показано взаимное положение
векторов, соответствующих основным гармоническим МДС катушек. Они сдвинуты в пространстве на угол. Их сумма дает
результирующее значение .Из построения на рис. 4.20, а нетрудно
получить выражение для первой гармоники
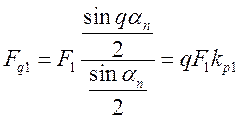 |
Аналогичным образом найдем третью гармонику^(рис. 4.20, б)
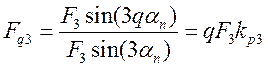 |
Здесь легко установить причину возрастающего влияния распределения обмотки на величину высших гармонических.
Вопрос 34,35.
Как можно выразить линейную плотность тока через магнитодвижущие силы. Приведите графическую интерпретацию.
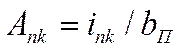 |
- поверхностная плотность( ток в пазу деленный на ширину паза.)
Поверхностный ток образуется после замены зубчатого
магнитопровода гладким и распределений тока каждого из пазов по поверхности
магнитопровода в виде слоя тонкого с линейной плотностью ![]() .
.
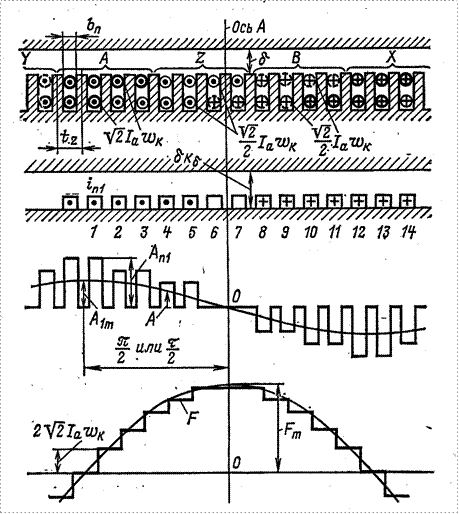 с изменением тока в пазах вид кривой плотности
поверхностного тока непрерывно меняется.
с изменением тока в пазах вид кривой плотности
поверхностного тока непрерывно меняется.
Поверхностную плотность тока удобно представить через магнитодвижущую силу.
Кривая МДС будет являться функцией от угла альфа(![]() ) и ее можно представить как интегральную
кривую распределения тока обмотки вдоль окружности статора.
) и ее можно представить как интегральную
кривую распределения тока обмотки вдоль окружности статора.
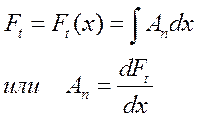 |
|||
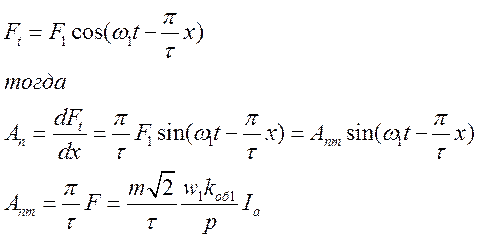 |
|||
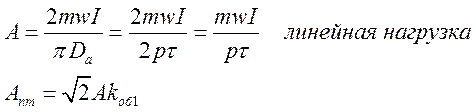
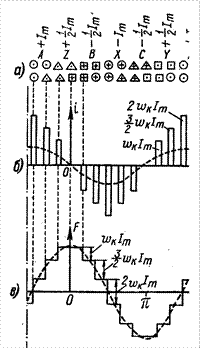
Аналогичное выражение можно записать и для любой высшей
гармоники линейной плотности тока .Каждая гармоника линейной плотности
поверхностного тока представляет собой вращающуюся волну с периодом ![]() и амплитудой
и амплитудой ![]() перемещающуюся
с той же угловой скоростью ,что и гармоника МДС.Волна плотности поверхностного
тока всегда смещена относительно волны МДС на величину
перемещающуюся
с той же угловой скоростью ,что и гармоника МДС.Волна плотности поверхностного
тока всегда смещена относительно волны МДС на величину ![]() против
часовой стрелки.
против
часовой стрелки.
Вопрос 36.
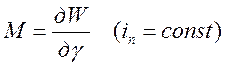
![]()
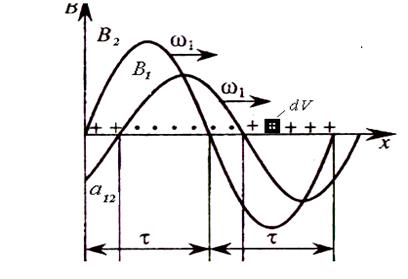
Однонаправленное преобразование энергий происходит только при условий вращения МДс или поля ротора с той же угловой скоростью в самой машине с какой вращается МДс статора и с одинаковым пространственным распределением. Преобразуемая энергия за период зависит от угла альфа12 между осями.Гамма-угол поворота ротора.
Вопрос 37.
При каких условиях образуется электромагнитный момент кАк результат взаимодеиствия гармоник индукций и поверхностной плотности тока.
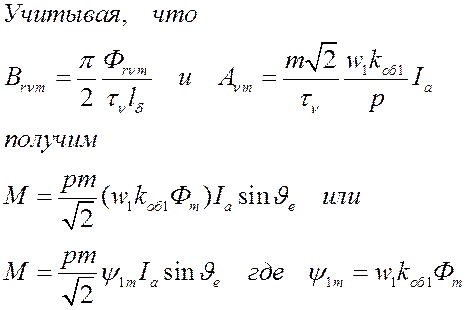 Электромагнитный момент образуется только
гармониками индукций и поверхностной плотностью тока имеющими одинаковую
скорость перемещения в воздушном зазоре и одинаковый порядок
гармоник(полюсность)
Электромагнитный момент образуется только
гармониками индукций и поверхностной плотностью тока имеющими одинаковую
скорость перемещения в воздушном зазоре и одинаковый порядок
гармоник(полюсность)
 |
|||
 |
|||
Вопрос 38.
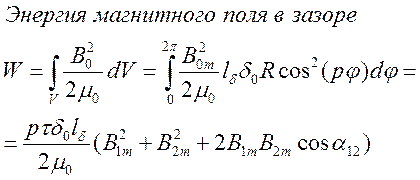
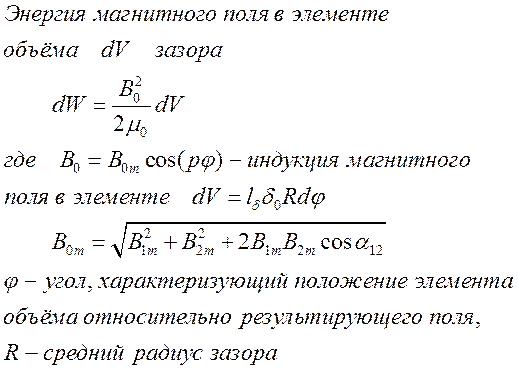 Как можно записать
выражение для энергий магнитного поля в воздушном зазоре.
Как можно записать
выражение для энергий магнитного поля в воздушном зазоре.
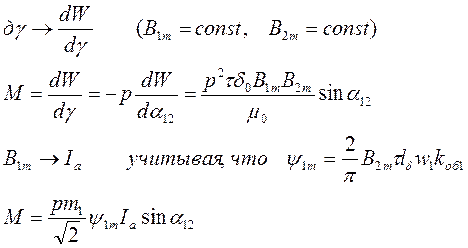
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.