Ответы на тестовые вопросы 1-38 по основам преобразования энергии в электрических системах

Вопрос 1

Двигатель имеет неподвижную часть, именуемую статором, и вращающуюся часть, называемую ротором. Сердечник статора собирают из стальных листов, изолированных друг от друга для уменьшения потерь на вихревые токи. В пазах статора размещают обмотку. Обмотка статора выполняется обычно трехфазной.

Вопрос 2

Сосредоточенной однофазной обмоткой называют такую, у которой q=1, где q- число пазов на полюс и фазу. В этом случае пазы располагают равномерно по окружности статора на расстоянии шага y, равного полюсному делению τ (y= τ).

Распределенная обмотка, это такая обмотка, у которой число пазов на полюс и фазу q=2,3…k. В данном случае активные стороны катушек одной фазы помещают не в одном пазу под полюсом, а в нескольких.

Обмоткой с укороченным шагом называют такую обмотку, шаг которой делают равным q=4/5, 6/7….

Вопрос 3

. Число пазов на полюс и фазу, это величина q, которая определяется выражением: 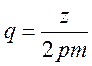, где z-число пазов, 2р- число пар полюсов, m-количество фаз.

Вопрос 4

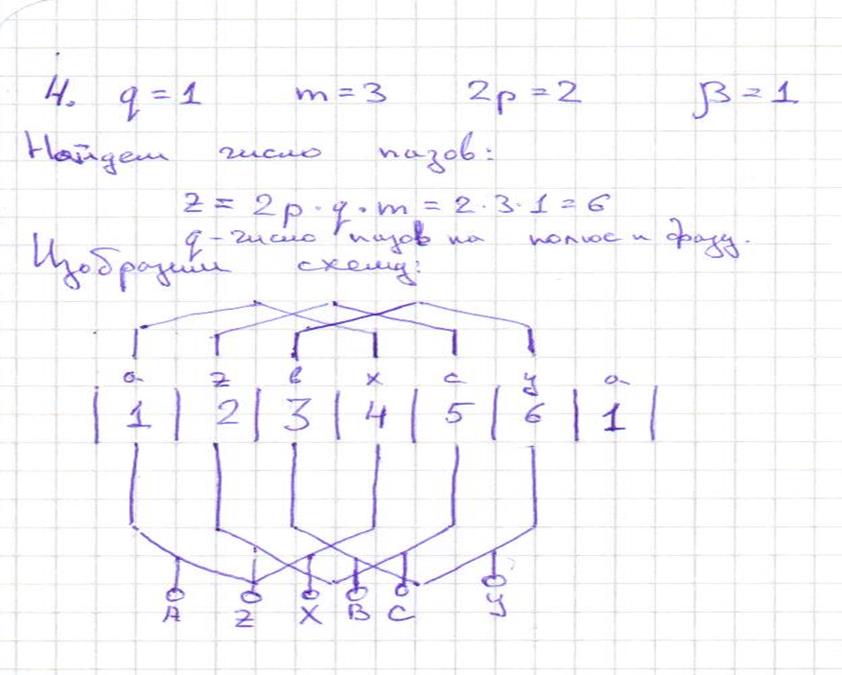
Вопрос 5

. Уменьшение ЭДС катушек за счет укорочения шага обмотки определяется коэффициентом укорочения kу, представляющим собой отношение ЭДС катушки с укороченным шагом к эдс катушки с полным шагом. Он будет равен 1, при равенстве вышеперечисленных ЭДС.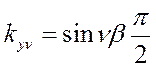

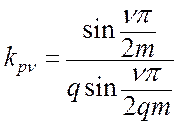А коэффициент распределения определяется следующим условием: электродвижущая сила распределенной в нескольких пазах обмотки меньше, чем э. д. с. сосредоточенной обмотки с тем же числом витков. Если эти ЭДС равны, то коэффициент равен 1.

                                         

Вопрос 6

Катушки выполнены из проводников, отстоящих друг от друга на шаг обмотки y, равный полюсному делению τ, то есть расстоянию между центрами разноименных полюсов. Такую обмотку называют обмоткой с полным или диаметральным шагом.

Для вывода формулы МДС катушки воспользуемся допущениями:

                                                                                           

 

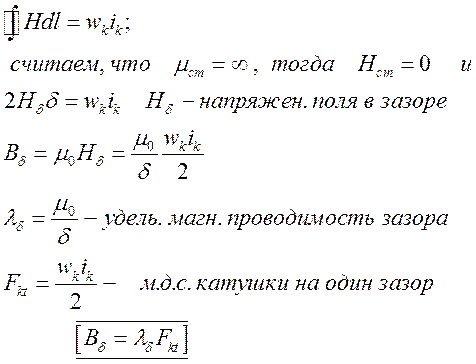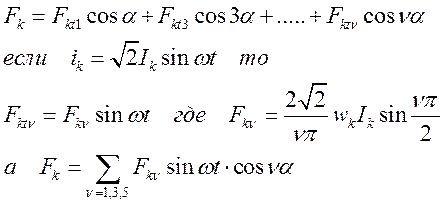Вопрос 7

 Согласно равенству для ряда катушек: 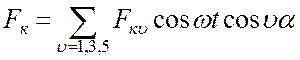, МДС рассматриваемого ряда катушексостоит из бесконечного ряда гармоник , каждая из которых изменяется в пространстве  и во времени по синусоидальному закону. Иными словами, МДС этого ряда катушек  представляет собой ряд неподвижных пространственных гармоник, амплитуды которых  пульсируют во времени по синусоидальному закону в пределах от + до -. Каждая гармоника МДС создает подобную же гармонику магнитного поля.

Вопрос 8

При диаметральном шаге (y=τ) катушка А-Х пронизывается всем магнитным потоком полюса, а при укороченном шаге (y<τ) катушки А-Х1 этот магнитный поток уменьшится. При диаметральном шаге ЭДС, индуктируемые в активных сторонах А и Х катушки, сдвинуты по фазе на 180 градусов, так что ЭДС катушки , представляющая собой геометрическую разность ЭДС ее активных сторон будет равна арифметической сумме этих ЭДС:

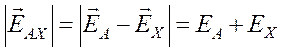
При укороченном шаге ЭДС активных сторон А и Х1 сдвинуты на угол, меньший 180 по фазе, и ЭДС катушки будет меньше арифметической суммы эдс этих сторон.

Вопрос 9

МДС катушки определяется выражениями:

 

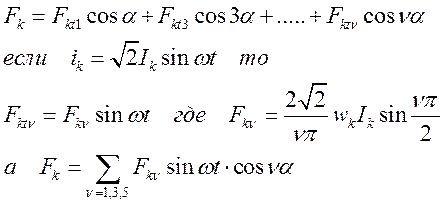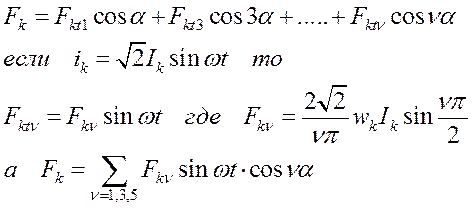А МДС фазы обмоток 

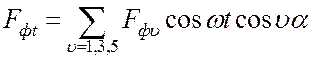
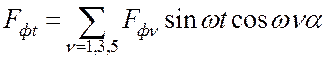
Вопрос 10

Для МДС фазы в целом действительно выражение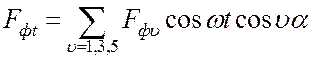

Его мы получили взяв выражение для МДС катушки ,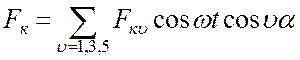

Заменив  ( амплитуда  гармоники МДС фазы обмотки(в вопросе 7 написано его значение).) на .

Согласно равенству для МДС фразы  представляет собой сумму неподвижных в пространстве и пульсирующих во времени гармоник.

Вопрос 11. Как можно представить МДС фазы в виде пространственных вращающихся волн?

Выражение для МДС фазы:

 

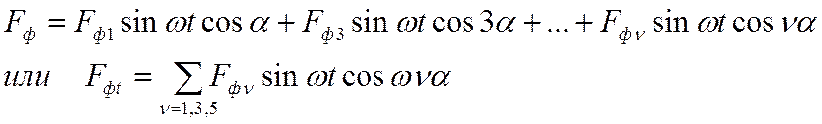Неподвижную пульсирующую во времени волну МДС фазы можно представить в виде:

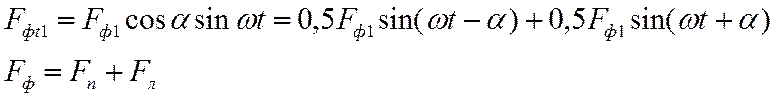
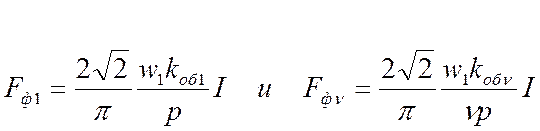Каждый из правых членов этого равенства представляет собой вращающуюся волну МДС, которая распределена в пространстве вдоль координаты α по синусоидальному закону и имеет амплитуду 0,5F_ф1

Вопрос  12. МДС трехфазной обмотки (на примере первой гармонической)

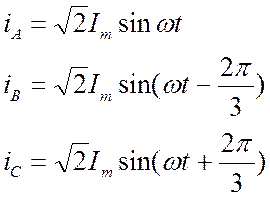Трехфазная обмотка с целым числом пазов на полюс и фазу нагружена симметричными токами:

Тогда вращающиеся волны первой гармонической МДС отдельных фаз выражаются равенствами:

 

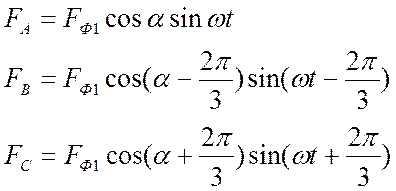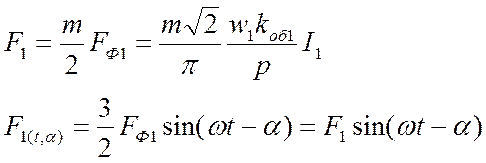В общем случае симметричная т-фазная обмотка при ее симметричной нагрузке создает только вращающиеся гармоники МДС, амплитуды которых на полюс равны:

Вопрос 13. Как рассчитываются МДС высших гармоник?