Основы аэродинамических и тепловых расчетов в электромеханике: Учебное пособие, страница 13

       - скорость движения потока на i-м участке.

Скорость движения охлаждающей среды неодинакова на различных участках охлаждающего тракта при заданном расходе и может быть выражена через сечение участка и расход

,

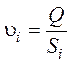где:  - расход охлаждающей среды,

       - сечение i-го участка.

В этом случае потери напора на i-м участке:

,

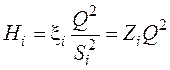где 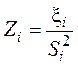 - аэродинамическое (или гидравлическое) сопротивление i-го участка, .

Коэффициент аэродинамического сопротивления принято выражать через коэффициент динамического давления:

где:  - коэффициент местного сопротивления.

Охлаждающий тракт электрической машины состоит из ряда участков, которые могут образовывать последовательные и параллельные цепочки, соединения треугольником и т.д.

Для расчета полного аэродинамического сопротивления охлаждающего тракта необходимо получить соотношения для различных комбинаций участков. При последовательном соединении расход на всех участках является одинаковым, а полный напор равен сумме напоров (рис. 3.7).

Если обозначить полное (аэродинамическое) сопротивление через , то получаем:

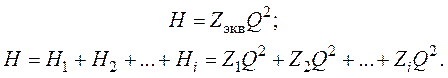
Таким образом, для последовательного соединения участков охлаждающего тракта получаем:

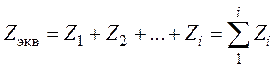
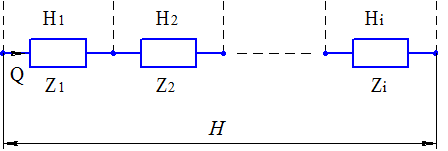
Рис. 3.7 Последовательное соединение участков охлаждающего тракта

При параллельном соединении участков одинаковым будет напор, а полный расход равен сумме расходов по участкам (рис. 3.8.).

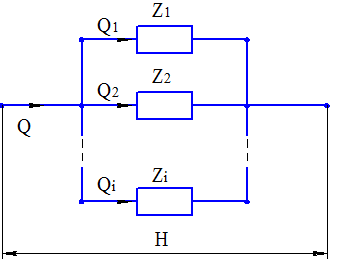
Рис. 3.8 Параллельное соединение участков охлаждающего тракта

Расход охлаждающей среды для всего тракта и отдельных участков определяется соотношениями:

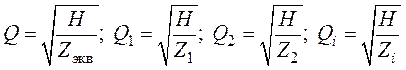
Так как , получим

.

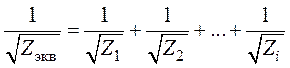Полное аэродинамическое сопротивление параллельно включенных участков определяется соотношением:

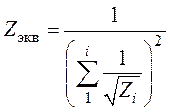
Ввиду нелинейной зависимости напора от расхода охлаждающей среды соотношения для преобразования соединения участков из треугольника в звезду (рис. 3.9) являются сложными и получены с некоторым приближением, что не позволяет обратным решением получить точные значения расхода в участках. Тем не менее такие преобразования используются в практических расчетах, особенно при расчете сложных разветвленных трактов охлаждения [3, 4].

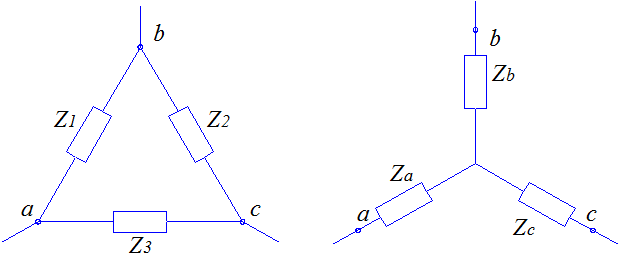
Рис. 3.9 Преобразование соединения участков треугольником в соединение звездой

Соотношение для расчета аэродинамических сопротивлений при преобразования треугольника в звезду (рис. 3.9) имеет вид:

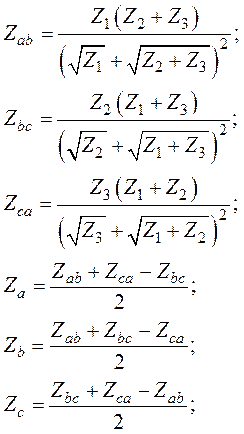
Зависимость полного напора в функции расхода охлаждающей среды

называется аэродинамической (гидравлической) характеристикой электрической машины. Для её построения необходимо рассчитать . Порядок его расчета следующий:

-  по компоновочному чертежу электрической машины определяются пути движения охлаждающей среды и составляется аэродинамическая (или гидравлическая) схема;

-  определяются сечения участков, коэффициенты местного сопротивления и рассчитываются аэродинамические (гидравлические) сопротивления участков;

-  рассчитывается эквивалентное аэродинамическое (гидравлическое) сопротивление тракта охлаждения и строится аэродинамическая (гидравлическая) характеристика).

Чем большее количество местных сопротивлений учтено при составлении аэродинамической схемы, тем точнее результаты расчета. Однако следует отметить, что это не всегда оправдано, т.к. значительно возрастает трудоемкость расчетов. Кроме того, следует иметь в виду, что точность расчета в большей мере определяется правильным выбором коэффициентов сопротивления, которые в основном определены экспериментальным путем на основе теории гидромеханического подобия.

3.4. Определение аэродинамических (гидравлических) сопротивлений тракта охлаждения.

Аэродинамическое (гидравлическое) сопротивление любого участка охлаждающего тракта определяется соотношением:

,

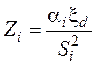где:  - коэффициент динамического давления;

       - коэффициент местного сопротивления.

Коэффициент динамического давления равен:

.

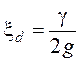В подавляющем большинстве электрических машин в качестве охлаждающей среды используется воздух. Величина коэффициента динамического давления соответственно равна:

,

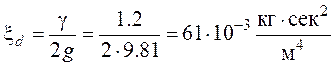где: =1.2 кг/м³  - удельный вес воздуха;

       м/сек² – ускорение силы тяжести.