изучение алгоритмического языка С. Изучение системы Matlab, страница 2

                             Цель работы

  1. Составление алгоритма вычисления суммы бесконечного  ряда с заданной  относительной точностью на основе суммы конечного числа членов.

  2. Вычисление очередного элемента ряда с использованием

  рекурентного соотношения.

                           Содержание и выполнение.

      Студенту предлагается вычислить одну из известных спецфункций по ее разложению в бесконечный ряд. Задается относительная точность на ограничение ряда.

   Рассмотрим простой пример:

   Вычислить Cos(x) по разложению в бесконечный ряд, с точностью eps.

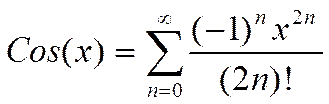         ;  |x|<=1; eps=10^-6.

   Для составления алгоритма вычисления суммы Вы должны четко представлять себе как вычисляется каждый элемент суммы.

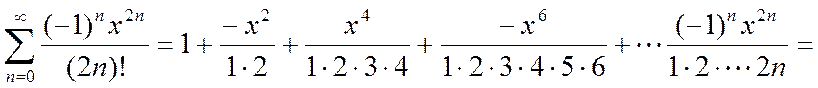    (1)

     = a₀+a₁+a₂+a₃+...+a_n+a_n+1+...a_¥.  

Анализ каждого члена ряда (a₁,a₂,a₃,...a_n,a_n+1 ..) и сравнение его с предыдущим показывает , что всегда ½a_n+1½<½a_n½ , т.е. последующий член меньше предыдущего - такие ряды в математике называются сходящимися. Сумма только сходящегося бесконечного ряда равна конечной величине. Сходимость ряда позволяет определить значение его бесконечной суммы с заданной относительной точностью,  вычислив сумму конечного числа членов.

    Итак, Cos(x) представлен суммой бесконечного числа элементов:

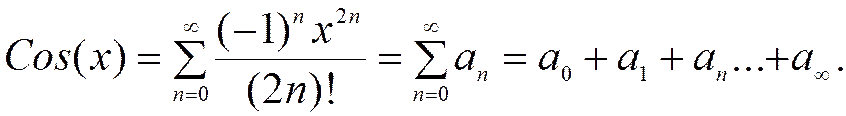
   Вы понимаете, что составлять алгоритм для вычисления бесконечного числа элементов не имеет смысла: ресурсы ЭВМ не оперируют с понятием бесконечность. С  другой стороны, и вычисление  бесконечно удаленного члена также не имеет смысла, так как он стремится к нулю. Действительно, если Вы попытаетесь вычислить сотый элемент:

                          

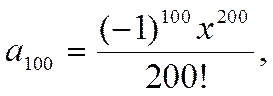
то получите очень маленькую величину, прибавление которой  к предыдущим  99 членам практически не изменит суммы, т.е. вычисление элементов с большими индексами и прибавление их к сумме теряет смысл, так как они очень малы по сравнению с суммой всех предыдущих элементов.

   Что значит очень малы? Это понятие должно иметь строгий математический смысл, т.е. должно быть выражено определенной величиной, которая и ограничит число элементов при вычислении суммы.

   Мы будем вычислять сумму не бесконечного числа членов, а конечного, это конечное число  m  определяется относительной точностью согласно соотношению:

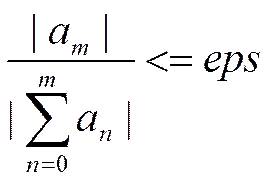                                     (2).

Предположим, eps=10^-6 . Отношение (2) говорит о том, что мы должны прекратить вычисление элементов и прибавление их к сумме, как только очередной элемент a_n=a_m будет меньше суммы из m элементов ряда в 10⁶ (1/eps)  раза. Прибавление следующего m+1 элемента не изменит величину суммы более чем на миллионную её часть.

В нашей задаче:

         

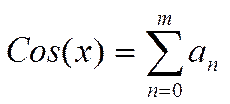
с точностью eps, где m определено согласно (2 ).

Вычисление очередного (текущего) члена.

Внимательно посмотрите разложение (1), ещё раз сравните последующий член с предыдущим и Вы убедитесь , что между соседними элементами существует рекуррентная связь: последующий член всегда можно выразить через предыдущий с помощью множителя постоянного вида (рекуррентного множителя). Действительно:

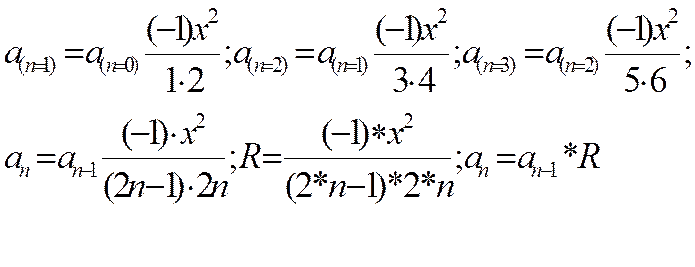
 -  рекуррентное соотношение.

Это рекуррентное соотношение и необходимо положить в основу вычисления текущего члена. Не вычислять x²ⁿ и (2n)! для каждого элемента, а использовать значение предыдущего и рекуррентное соотношение.  

   Итак, словесный алгоритм:

1. Начало.

2. Полагаем n=0, вычисляем нулевой член  a_n=0 , вычисляем сумму S.

 ( n=0; a=1; S=a ).

3.Увеличиваем n на 1 (n=n+1).

4.Вычисляем рекуррентный множитель R=-1*x²/((2*n-1)*2*n) .

5.Вычисляем следующий член: a=a*R.                             

6. Прибавляем его к сумме: S=S+a .

7. Проверяем соотношение:

               |a| / |S| <=eps

   Если соотношение ложь,т.е. очередной член по сравнению с   суммой еще велик , то необходимо вернуться к пункту 3 и продолжить накопление суммы.

   Если соотношение истина , т.е. очередной вычисленный член    меньше накопленной суммы в 1 /eps  раз , то вычисление заканчивается, а накопленная сумма и есть результат – переход к пункту 8.