Расчет и построение графика напряжения u2(t) на выходе цепи с помощью интеграла Дюамеля

Введение 

          Среди дисциплин, составляющих основу базовой подготовки специалистов в области связи, важнейшее место отводится курсу «Основы теории электрических цепей» (ОТЦ). Одним из основоположников курса теории электрических цепей был доктор технических наук, профессор А.Ф. Белецкий, внесший большой вклад в ее становление как самостоятельной дисциплины.

  Содержание этой дисциплины составляют задачи  анализа и синтеза линейных и нелинейных электрических цепей,  изучение как с качественной, так и количественной стороны установившихся и переходных процессов, протекающих в различных электронных  приборах и устройствах. Современные эффективные аналитические методы анализа электрических це­пей основаны в конечном счёте на сочетании законов Кирхгоффа, которым удовлетворяют токи и напряжения в электрических цепях, с теорией дифференциальных уравнений. Находят широкое применение и численные методы анализа электрических цепей, в которых реализу­ются алгоритмы решения уравнений, связывающих между собой напряжения и токи в анали­зируемой цепи.

Высокий уровень развития расчётных методов теории электрических цепей и совершен­ство оптимальных методов их синтеза обязаны использованию применительно к соответст­вующим задачам фундаментальных исследований русских и советских математиков.

         ОТЦ  базируется на курсах математики, физики, технической электроники, вычислительной техники и является базовым для изучения последующих общетехнических и специальных дисциплин.

Целью данной курсовой работы является систематизация и закрепление знаний, полу­ченных  студентами при изучении классического, операторного и спектрального методов рас­чёта процессов в линейных электрических цепях, а также теоретических основ анализа дис­кретных сигналов и линейных дискретных цепей.

Методы анализа работы узлов аппаратуры связи

1. Временной метод анализа

1.1 Определение переходной и импульсной характеристик

Операторный метод. Операторная схема замещения для определения переходной характеристики, соответствующая схеме (рисунок 1.2), приведена на рисунке 1.3.

Изображение G(p)преходной характеристики g(t) равно изображению напряжения U₂(p) и  

определяется на основании закона Ома:

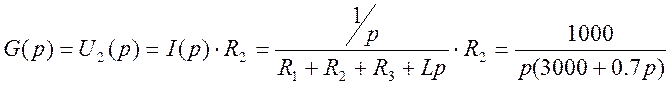                               (1.12)

                                                                                                 (1.13)

            Операторная схема замещения для определения импульсной характеристики приведена на рисунке 1.4. изображение импульсной характеристики H(p) отыскивается в следующем виде:

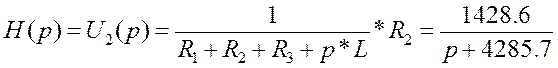                                                   (1.14)

                                                                                                         (1.15)

Полученные операторным методом выражения для g(t) и h(t) (формулы 1.14 и1.15) идентичны выражениям, полученным классическим методом. Графики переходной и импульсной характеристики приведены на рисунках 1.5 и 1.6.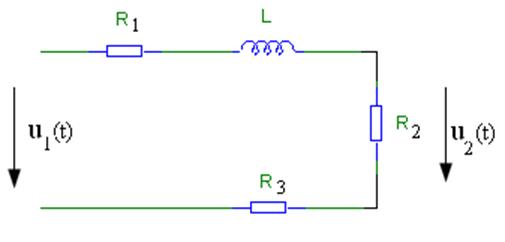

Рисунок 1.1 – Схема анализируемой цепи

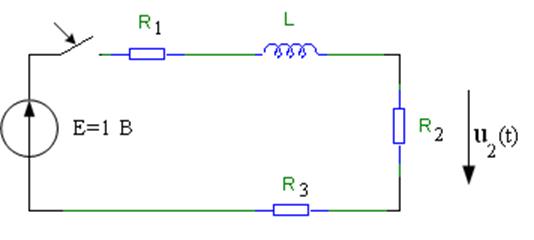
Рисунок 1.2 – Схема для определения переходной характеристики

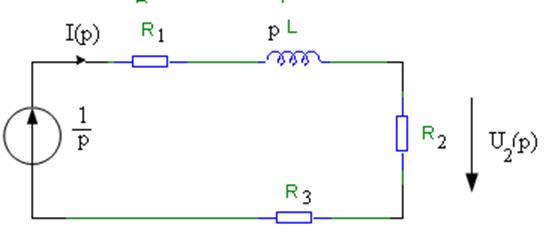
Рисунок 1.3 – Операторная схема замещения для определения переходной характеристики

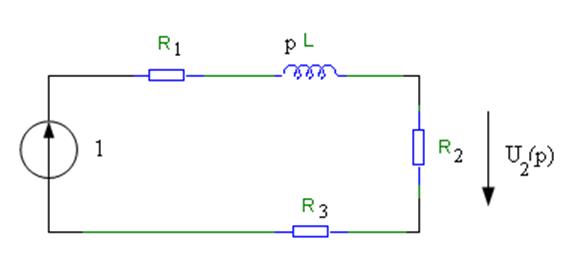
Рисунок 1.4 - Операторная схема замещения для определения импульсной характеристики

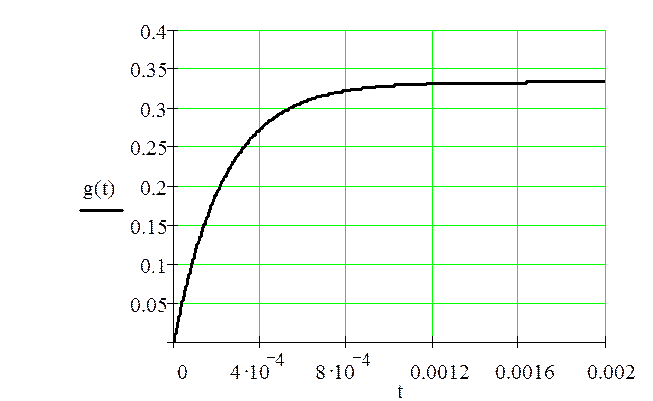
Рисунок 1.5 - Переходная характеристика

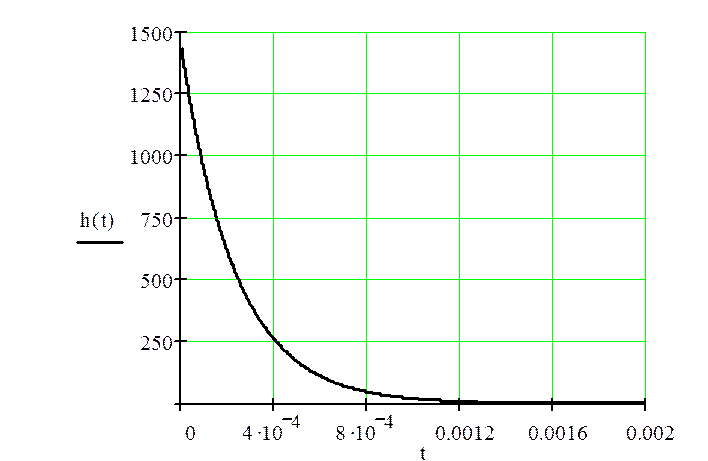
Рисунок 1.6  - Импульсная характеристика

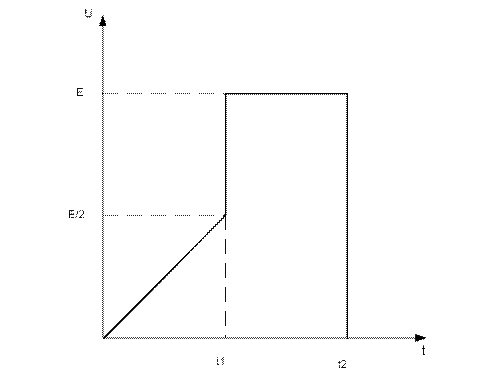
Рисунок 1.7 - Входное воздействие

1.2  Вычисление реакции цепи с помощью интеграла Дюамеля

Для входного сигнала (рисунок 1.7) известно:  Е=10 В, t₁=0.002 с, t₁=0.004 с. Представим входной сигнал в виде функции времени:

u₁(t)=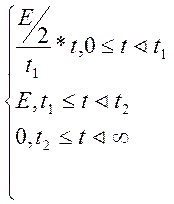                                                                                                        (1.16)

Подставляя параметры заданного сигнала, получим:

u₁(t)= 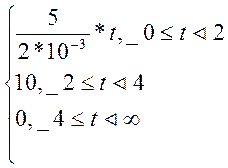                                                                                              (1.17)

Значения производных входного сигнала на каждом интервале времени:

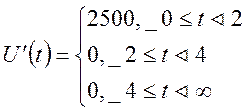                                                                                                      (1.18)

Найдем входное напряжение u₂(t) на каждом интервале времени методом интеграла Дюамеля:

             I интервал:

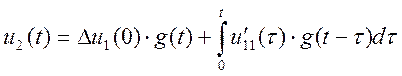
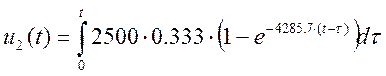       , B                                                                     (1.19)

             II интервал:

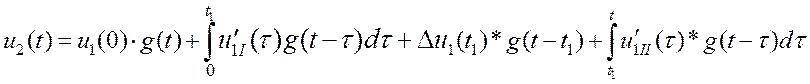          (1.20)

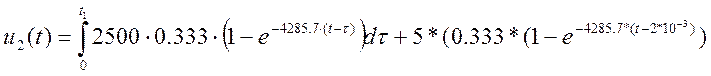
, B                   (1.21)

III интервал:

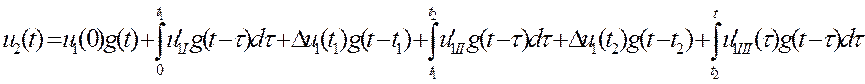 (1.22)                                                                                                                                                 

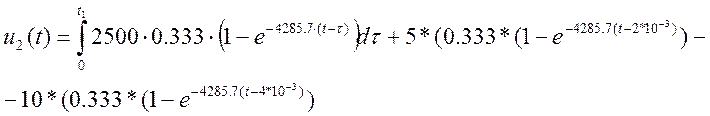                           (1.23)

Результаты расчетов, выполненные по формулам 1.19, 1.21, 1.23, приведены в таблице 1.1, по ним построен график u₂(t) (рисунок 1.8).

Таблица 1.1 – Значения выходного сигнала U₂(t) от времени

t, мс	0	0.4	0.8	1.2	1.6	t1-	t2+
u2(t), B	0	2.55	2.74	2.52	2.2	1.87	1.87
t, мс	2.4	2.8	3.2	3.6	t2-	t2+	t2+4t
u2(t), B	1.025	0.87	0.84	0.835	0.83	0.83	0

Рисунок 1.8 - Выходной отклик

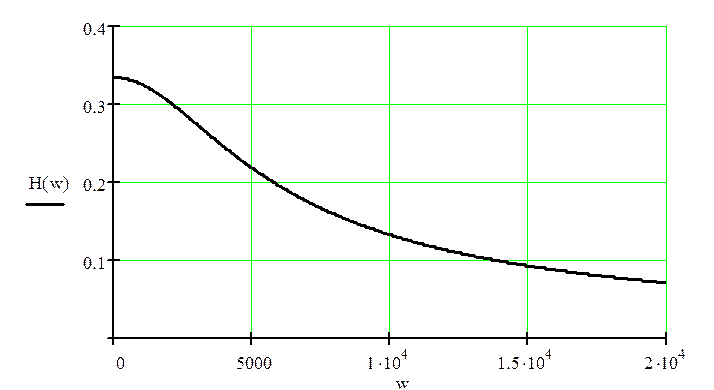
Рисунок 2.1 – Амплитудо-частотная характеристика цепи

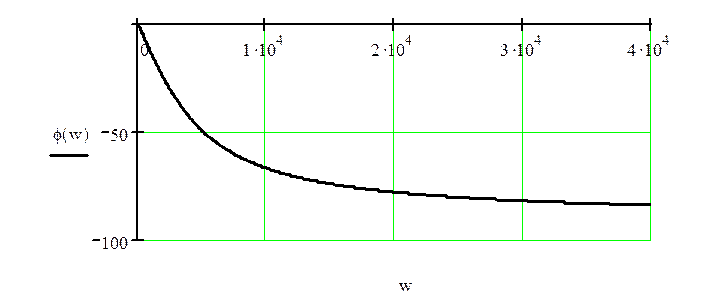
Рисунок 2.2 – Фазо-частотная характеристика цепи

2. Спектральный метод анализа

2.1 Определение комплексной передаточной функции цепи