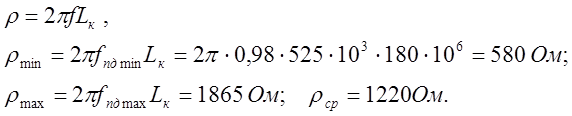
7. Резонансное сопротивление контура без учёта шунтирующих влияний можно найти, задавшись конструктивной добротностью (Qк = 80)
.
8. Далее необходимо выбрать вид связи контура со входом первого активного элемента. Рассмотрим вначале случай автотрансформаторной связи контура со входом транзистора (пренебрегая шунтирующим влиянием антенны)
,
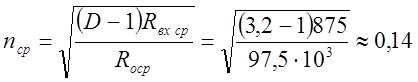где
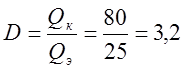
Qэ - известно из расчёта структурной схемы (см. пример из п. 2.3.1.).
Расчёт произведён для средней частоты поддиапазона fср = 1065 кГц.
9. Найдём эквивалентную добротность контура на границах поддиапазона
;
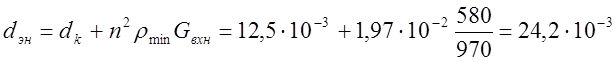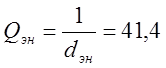на
частоте fmin = 525 кГц.
;
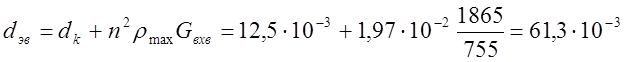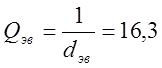на частоте fmax = 1605 кГц.
Отсюда видно, что изменения эквивалентной добротности контура вследствие шунтирующего влияния транзистора превышают границы допустимого из условия заданной неравномерности в полосе пропускания на нижнем конце поддиапазона и избирательности по зеркальному каналу на верхнем конце диапазона (19 < Qэ < 31).
10. Проверим избирательность по зеркальному каналу и неравномерность в полосе
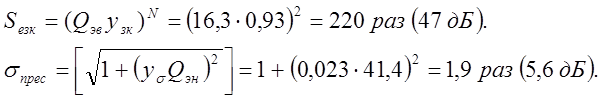
Как видим, требования на избирательность по зеркальному каналу и неравномерность в полосе пропускания преселектора, заданные техническими условиями (пример из п.2.3.1.), не выполняются вследствие резкого изменения добротности контуров преселектора в пределах поддиапазона. Этот недостаток можно устранить, если взять частотно-зависимую связь контура со входом первого транзистора, например, внутренне-емкостную и трансформаторную (рис. 3). При такой связи можно обеспечить постоянство или даже некоторое увеличение эквивалентной добротности контура на верхнем конце поддиапазона.
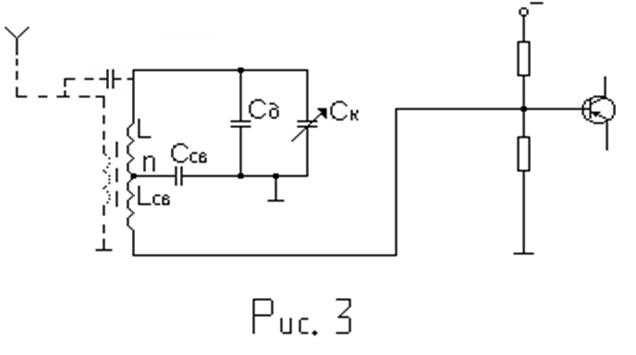
11. Рассчитаем элементы связи контура со входом транзистора по схеме рис. 3 из условия постоянства эквивалентной добротности (Qэ = 25) в пределах поддиапазона.
Коэффициент трансформации соответственно на нижнем и верхнем конце поддиапазона
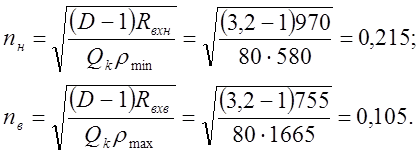
Вспомогательный коэффициент
.
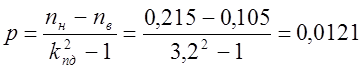Ёмкость конденсатора связи
.
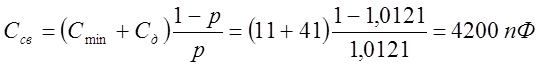Индуктивность катушки связи
.
Такими будут Ссв и Lсв во входной цепи. В контуре УРЧ они могут быть другими, т. к. Rвх следующего каскада, например, смесителя будет отличаться от Rвх усилителя. Если выбрана двухконтурная входная цепь, то связь между контурами целесообразно выполнять внутренне-емкостную или комбинированную.
При использовании в качестве первого активного элемента приёмника полевого транзистора применяется полное включение контура ко входу триода (n = 1).
Задано: Диапазон частот f = 11,4…12,1 МГц; Ск max = 450 пФ; Ск min = 15 пФ;
СL=2 пФ; СМ1 = 10 пФ; СПср = 20 пФ, - средняя величина ёмкости подстроечного конденсатора; Нс = 15 - неравномерность закона изменения ёмкости Ск от угла поворота роторных пластин.
1. Определим коэффициент поддиапазона
.
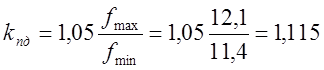2. Определим ёмкость С3 и С~
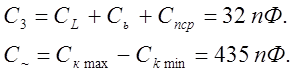
3. Рассчитаем ёмкость С2 [4, с. 232; 5, с. 18]
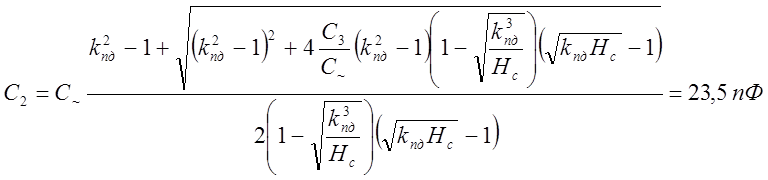
Берём номинал по ГОСТ С2 = 24 пФ.
4. Для определения С1 найдём вспомогательные коэффициенты
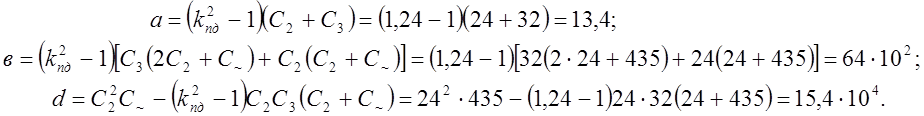
5. Рассчитаем ёмкость С1
.
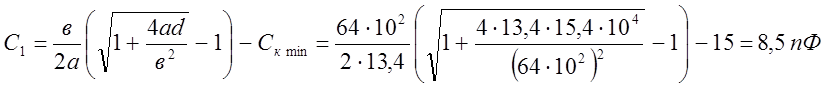Берём номинал С1 = 8,2 пФ.
6. Проверим коэффициент перекрытия поддиапзона
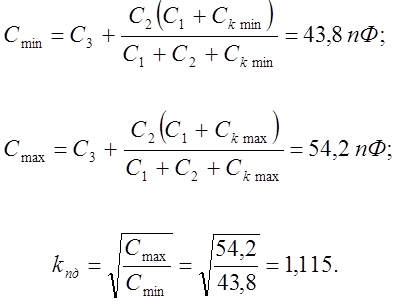
Точность расчёта не хуже ± 10% приемлима.
7. Индуктивность контура
.
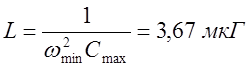Дальнейший расчёт аналогичен приведйнному в предыдущем примере.
Методика расчёта входных цепей с той или иной степенью полноты содержится в рекомендованных пособиях [1…6]. Предварительно схема входной цепи была выбрана при расчёте структурной схемы приёмника. После расчёта параметров входного контура (п.3.1), необходимо определить элементы связи контура с антенной, коэффициент связи, коэффициент передачи входной цепи на верхнем и нижнем конце поддиапазона и неравномерность передачи в пределах рассчитываемого поддиапазона.
Для ненастроенных антенн резонансный коэффициент передачи определяется выражением [11, гл. 3; 12, гл. 4]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.