35 ОЦЕНКА ЭФФЕКТИВНОСТИ КАНАЛА СВЯЗИ
12.2. Характеристики и показатели эффективности СПИ
В общем случае эффективность любой системы определяется количеством и качеством выдаваемой продукции. В СПИ такой продукцией является передаваемая информация. Количество её определяется средней скоростью передачи информации Rи (бит/c), а качество – величиной ошибки. Согласно теореме оптимального кодирования [1] в принципе всегда можно обеспечить вероятность ошибки p £ pдоп , где pдоп- ее допустимое значение. Скорость передачи информации Rи не может быть больше пропускной способности канала С´. Отсюда следует, что важнейшим показателем эффективности СПИ является скорость передачи информации Rи, при которой обеспечивается заданная верность передачи (ошибка pдоп).
Наиболее общей характеристикой эффективности систем связи является информационная эффективность.
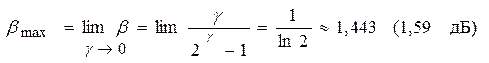 |
|||
 |
Необходимые скорость и верность передачи получают определёнными затратами мощности сигнала Pс и полосы частот канала F. Поэтому вводят ещё два показателя:
1)Энергетическую эффективность- коэффициент, характеризующий использование канала по мощности где N0 – спектральная плотность шума;
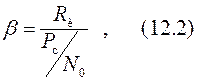 |
2)Частотную эффективность - коэффициент, характеризующий использование канала по полосе частот
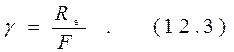 |
Безразмерные коэффициенты b и g имеют смысл удельных скоростей: количество бит/c , приходящихся на 1 Вт мощности сигнала, отнесённое к спектральной плотности шума и количество бит/c, приходящееся на 1 Гц полосы частот канала. Обратные величины определяют количество Ватт, отнесённое к N0 и, соответственно, количество Герц, затрачиваемых на передачу 1 бит/c информации.
Установим связь между показателями эффективности h, b и g. Для гауссовского непрерывного канала (ГНК) согласно формуле Шеннона
С¢= F×log 2 (r+1), где r = Pc /Pш - отношение средних мощностей сигнала и шума; для квазибелого шума Pш = N0 ×F. Тогда в соответствии с выражениями (12.1), (12.2), (12.3) получаем
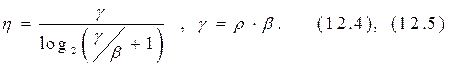 |
Согласно теореме Шеннона при соответствующих способах передачи (кодирования и модуляции) и приёма (демодуляции и декодирования) величина hпри сколь угодно малой вероятности ошибок может быть сколь угодно близкой к единице. При h=1 получаем предельную зависимость между b и g :
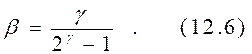 |
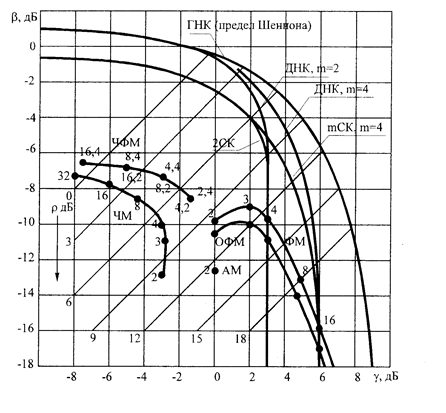
Эту зависимость удобно представить на плоскости в координатах bи g (рис.12.1). Кривая ГНК является предельной и показывает наилучший обмен между bи g в гауссовском непрерывном канале. Следует отметить, что частотная эффективность g изменяется в пределах от 0 до ¥ , в то время как энергетическая эффективность b ограничена сверху
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.