Математические методы теории информации. Оптимизация на графах. Передача информации. Оптимальное статическое кодирование сообщений. Помехоустойчивое кодирование

СОДЕРЖАНИЕ

1.     МАТЕМАТИЧЕСКИЕ МЕТОДЫ ТЕОРИИ ИНФОРМАЦИИ.......... 2

Задача 1....................................................................................................... 3

2.     ОПТИМИЗАЦИЯ НА ГРАФАХ........................................................... 4

Задача 2....................................................................................................... 4

3.     ПЕРЕДАЧА ИНФОРМАЦИИ............................................................... 5

Задача 3 (А)................................................................................................. 6

Задача 3 (Б)................................................................................................. 7

4.     ОПТИМАЛЬНОЕ СТАТИЧЕСКОЕ КОДИРОВАНИЕ СООБЩЕНИЙ................................................................................................ 8

Задача 4....................................................................................................... 9

Задача 5 (А)............................................................................................... 10

Задача 5 (Б)............................................................................................... 11

5.     ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ.................................... 13

Задача 6..................................................................................................... 15

ЛИТЕРАТУРА.............................................................................................. 18

1.  МАТЕМАТИЧЕСКИЕ МЕТОДЫ ТЕОРИИ ИНФОРМАЦИИ

Вероятность - это событие, которое может произойти или не произойти  в результате опыта. Если при n-кратном повторении какого-либо опыта относительная частота i-ого события по мере увеличения количества испытаний стремится к некоторому пределу:

                                                                                                                  [1.1]

Число Pi позволяет при этом количественно сравнивать события по степени их возможности и называется вероятностью.

Достоверное событие - такое, которое непременно должно произойти. Невозможное событие - это такое событие, которое в данном опыте не произойдёт. В большинстве практических случаев мы сталкиваемся со сложными событиями, представляющих собой сложное сочетание из хода разных событий. Используют косвенную оценку вероятности сложных событий через известные вероятности событий, логически связанных с тем. Систему таких косвенных оценок изучает теория вероятности.

Исходные понятия:

Несовместные события - это такие два события, которые в данном опыте не могут появиться вместе. Если мы имеем события и в результате реализации появляется хотя бы одно из них, то такая группа событий называется полной.

Противоположные события - это два несовместных события.

Независимые события - такие, если вероятность появления одного из них не зависит от того, имело место или нет другое событие.

Зависимые события - такие, если вероятность появления события А зависит от того, имело ли место событие В. В этом случае вводят понятие условной вероятности Р(А/В).

Суммой нескольких событий называется событие, заключающееся в появлении хотя бы одного из них.

Произведение нескольких событий - это событие, заключающееся в совместном появлении всех событий.

Свойства: (в основе косвенных методов оценки вероятностей лежат две теоремы)

1. Теорема сложения вероятностей. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:

P(A1+A2+...+An) = P(Ai)                                                                                             [1.2]

2. Теорема умножения вероятностей. Вероятность произведений двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что имело место первое событие:

                                                                                                             [1.3]

Частный случай: Если события А и В независимы, то условная вероятность равна безусловной вероятности.

Рассмотрим две группы событий: А и В - несовместные события. В этом случае полная вероятность события Аi (вероятность того, что событие Аi появится с любым из группы Вi) определяется суммой вероятности произведений по параметру j-ое:

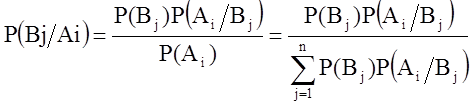                                                                  [1.4]

 [1.4] - формула Байеса.

Вероятностные характеристики. Если случайная величина x непрерывна и может принимать любое значение в интервале [x_min ,x_max], то её статистической характеристикой может служить интегральный закон распределения:

xÎ[x_min , x_max  ]      F(x) = P(x  < X)                                                                                        [1.5]

F(x) - это вероятность того, что значение случайной величины x меньше наперёд заданного x.

Вероятность попадания на интервал:

P(x1 £ x £ x2) = F(x2) - F(x1)                                                                                                [1.6]