Изучение вероятностных закономерностей массовых однородных случайных событий

 ОПРЕДЕЛЕНИЯ,  ФОРМУЛЫ  И  ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

2.1. Краткие теоретические сведения к контрольной работе 9

2.1.1. Определения и формулы к решению задач 311 – 320

          Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

          Случайным называют событие, которое в данном опыте (эксперименте) может либо произойти, либо не произойти. Например, выпадение герба при одном бросании одной монеты – событие случайное.

          Достоверным называют событие, которое в данном опыте обязательно произойдет. Невозможным называют событие, которое не может осуществиться в эксперименте. Например, выпадение не более восьми очков при бросании игральной кости – достоверное событие, а выпадение восьми очков – невозможное.

          Если некоторый опыт уже проведен п раз и реально наблюдалось m раз появление случайного события А, то число

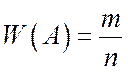                                                     (2.1)

называют относительной частотой события А. Например, случайное событие    А − выпадение герба при 100 бросаниях монеты произошло 45 раз. Значит, частота . При повторении 100 бросаний монеты, скорее всего, число выпадений герба m будет другим. Таким образом, относительная частота  случайного события А может менять значение, однако ясно, что при большом числе серий опытов с бросанием монеты значения относительной частоты  будут достаточно близки к числу 0,5. Это обстоятельство в повседневной жизни выражают словами «шансы выпадения герба при одном бросании монеты один к одному или 50 %» или «вероятность выпадения герба равна 0,5». В этом и состоит опытная, статистическая основа теории вероятностей.

          Рассмотрим классическое определение вероятности.

          События  называют несовместными, если в одном испытании (опыте) может произойти не более одного из этих событий.

События  образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Если равновозможные события образуют полную группу несовместных событий, то их называют элементарными исходами и обозначают .

Например, при бросании игральной кости за элементарные исходы можно принять случайные события , где  – число выпавших очков.

Элементарные исходы, в которых конкретное событие наступает, называют благоприятствующими этому событию. Например, при бросании игральной кости может наступить событие А – выпадение не менее пяти очков. Тогда благоприятствующими этому событию будут исходы .

Вероятностью события А называют число

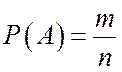,                                                               (2.2)

где п – общее число элементарных исходов;

m – число исходов, благоприятствующих событию А.

          По этому классическому определению вероятность выпадения не менее пяти очков при бросании игральной кости .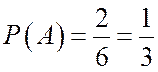

          Назовем три важнейших свойства вероятности.

          С в о й с т в о  1.  Вероятность достоверного события равна единице.

          С в о й с т в о  2.  Вероятность невозможного события равна нулю.

          С в о й с т в о  3.  Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

          З а д а ч а  1. Бросают две игральные кости. Найти вероятность того, что а) произведение выпавших очков − не более 8; б) сумма выпавших очков     кратна 4.

          Р е ш е н и е.

Рассмотрим случайные события:

А – произведение выпавших очков − не более 8;

В – сумма выпавших очков кратна 4;

 – на первой кости выпало i очков, на второй – j.

Все 36 событий  равновозможные, несовместны и образуют полную группу, т. е. являются элементарными исходами. Перечислим их:

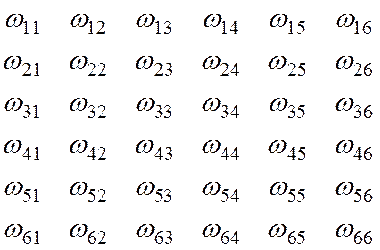
          Событию А благоприятствуют 16 элементарных исходов:

          Событию В благоприятствуют девять элементарных исходов:

          По формуле (2.2) получаем значения вероятности: , .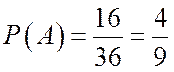

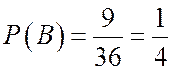2.1.2. Определения и формулы к решению задач 321 – 330

          Формула (2.2) позволяет найти вероятности достаточно простых событий. Рассмотренные ниже теоремы сложения и умножения вероятностей помогают найти вероятности более сложных событий.

          Суммой событий А и В называют событие , состоящее в появлении события А или события В, или обоих этих событий.

          Пусть имеется две урны, в каждой из которых есть красные и синие шары. Из каждой урны извлекают по одному шару. Тогда событие С – среди двух извлеченных шаров окажется хотя бы один красный − является суммой двух событий: А₁ − из первой урны извлечен красный шар − и А₂ − из второй урны извлечен красный шар.

          Произведением событий А и В называют событие , состоящее в совместном появлении обоих этих событий. В примере с двумя урнами произведением событий А₁ и А₂ будет событие D – оба извлеченных шара оказались красными.

Условной вероятностью  называют вероятность события В, вычисленную в предположение, что событие А уже произошло. В примере с урнами на значение вероятности , очевидно, никак не скажутся сведения о том, что событие А₁ произошло или не произошло, т. е. .

          Если вероятности  и  равны, то события А и В называют независимыми.

          Противоположными называют события А и , которые несовместны и образуют полную группу событий. Например, противоположными являются события А₁ – из первой урны извлечен красный шар − и  – из первой урны извлечен синий шар. Также противоположными будут события С – среди двух извлеченных шаров окажется хотя бы один красный − и Е – оба извлеченных шара синие.

          Т е о р е м а  1.