



Санкт-Петербургский Государственный Университет Низкотемпературных и Пищевых Технологий
Кафедра экономики промышленности и организации производства

Коляда В. А.
шифр К4834
Санкт-Петербург 2004
Решить задачу линейного программирования симплексным методом.
max (3x1 + 2x2 + x4)
x1 + 4x2 + 2x4 £ 100
2x1 – 3x2 – x3 + 3x4 £ 130
x2 + 2x3 – x4 £ 150
x(j) >= 0
Решение:
Вводим остаточные переменные S1³ 0; S2 ³ 0; S3 ³ 0, в результате чего исходные неравенства обращаются в равенства:
х1 + 4х2 +2х4 + S1 = 100
2x1 – 3x2 – x3 + 3x4 + S2 = 130
![]() x2 + 2x3 – x4 + S3
= 150
x2 + 2x3 – x4 + S3
= 150
Z = 3x1 +2x2 + x4 + 0*S1 + 0*S2 + 0*S3 = 0
![]() Z – 3x1 – 2 x2 –
x4 – 0*S1 – 0*S2 – 0*S3 = 0
Z – 3x1 – 2 x2 –
x4 – 0*S1 – 0*S2 – 0*S3 = 0
x1 + 4x2 + 2x4 +S1 = 100
2x1 – 3x2 – x3 + 3x4 + S2 = 130
x2 + 2x3 – x4 S3 = 150
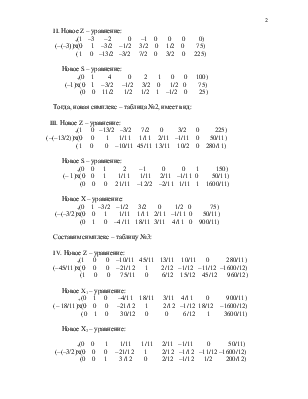
I. Составим симплекс – таблицу №1:
1. Сформулируем ведущее уравнение (Условие оптимальности вводимой переменной является небазисная переменная, имеющая в Z – уравнении наибольший отрицательный коэффициент. Условие допустимости. Исключаемой переменной выбирается та базисная переменная, для которой отношение постоянной в правой части к коэффициенту ведущего столбца минимально).
2. Сформулируем все новые уравнения. (Новое уравнение = предыдущее уравнение – [коэффициент ведущего столбца предыдущего уравнения] * (новая ведущая строка). В результате все остальные коэффициенты ведущего столбца становятся = 0
II. Новое Z – уравнение:
+(1 –3 –2 0 –1 0 0 0 0)
(–(–3))х(0 1 –3/2 –1/2 3/2 0 1/2 0 75)
(1 0 –13/2 –3/2 7/2 0 3/2 0 225)
Новое S – уравнение:
+(0 1 4 0 2 1 0 0 100)
(–1)х(0 1 –3/2 –1/2 3/2 0 1/2 0 75)
(0 0 11/2 1/2 1/2 1 –1/2 0 25)
Тогда, новая симплекс – таблица №2, имеет вид:
III. Новое Z – уравнение:
+(1 0 –13/2 –3/2 7/2 0 3/2 0 225)
(–(–13/2))х(0 0 1 1/11 1/11 2/11 –1/11 0 50/11)
(1 0 0 –10/11 45/11 13/11 10/2 0 280/11)
Новое S – уравнение:
+(0 0 1 2 –1 0 0 1 150)
(– 1)х(0 0 1 1/11 1/11 2/11 –1/11 0 50/11)
(0 0 0 21/11 –12/2 –2/11 1/11 1 1600/11)
Новое Х – уравнение:
+(0 1 –3/2 –1/2 3/2 0 1/2 0 75)
(–(–3/2)х(0 0 1 1/11 1/11 2/11 –1/11 0 50/11)
(0 1 0 –4 /11 18/11 3/11 4/11 0 900/11)
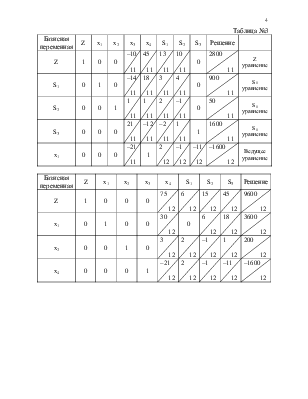
Составим симплекс – таблицу №3:
IV. Новое Z – уравнение:
+(1 0 0 –10/11 45/11 13/11 10/11 0 280/11)
(–45/11)х(0 0 0 –21/12 1 2/12 –1/12 –11/12 –1600/12)
(1 0 0 75/11 0 6/12 15/12 45/12 960/12)
Новое X1 – уравнение:
+(0 1 0 –4/11 18/11 3/11 4/11 0 900/11)
(– 18/11)х(0 0 0 –21/12 1 2/12 –1/12 18/12 –1600/12)
(0 1 0 30/12 0 0 6/12 1 3600/11)
Новое Х2 – уравнение:
+(0 0 1 1/11 1/11 2/11 –1/11 0 50/11)
(–(–3/2)х(0 0 0 –21/12 1 2/12 –1/12 –11/12 –1600/12)
(0 0 1 3 /12 0 2/12 –1/12 1/2 200/12)
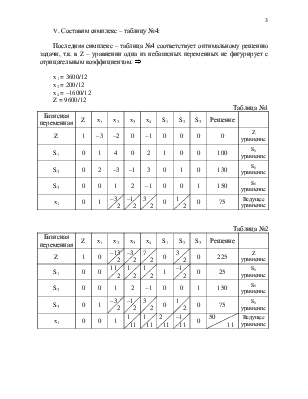
V. Составим симплекс – таблицу №4:
Последняя симплекс – таблица №4 соответствует оптимальному решению задачи, т.к. в Z – уравнении одна из небазисных переменных не фигурирует с отрицательным коэффициентом. Þ
x1 = 3600/12
x2 = 200/12
x4 = –1600/12
Z = 9600/12
Таблица №1
|
Базисная переменная |
Z |
x1 |
x2 |
x3 |
x4 |
S1 |
S2 |
S3 |
Решение |
|
|
Z |
1 |
–3 |
–2 |
0 |
–1 |
0 |
0 |
0 |
0 |
Z уравнение |
|
S1 |
0 |
1 |
4 |
0 |
2 |
1 |
0 |
0 |
100 |
S1 уравнение |
|
S2 |
0 |
2 |
–3 |
–1 |
3 |
0 |
1 |
0 |
130 |
S1 уравнение |
|
S3 |
0 |
0 |
1 |
2 |
–1 |
0 |
0 |
1 |
150 |
S1 уравнение |
|
x1 |
0 |
1 |
–3 2 |
–1 2 |
3 2 |
0 |
1 2 |
0 |
75 |
Ведущее уравнение |
Таблица №2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.