





ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО СВЯЗИ И ИНФОРМТИЗАЦИИ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ
Кафедра ПМ и К
Курсовая работа
«Расчет характеристик электрической цепи»
Выполнила:
студентка группы М-91 Гуреева Мария
Проверил:
Рягин Борис Алексеевич.
Новосибирск, 2010 г.
Задание.
Измерение заряда (У) на некотором конденсаторе описывается дифференциальным уравнением.
y’=k*х+y
y(0)=l, k=2, l=0.2+2*0.1+1/1000;
Составить программу, вычисляющую силу тока I≈∆y/∆x=∆y/h при х=0.05, x=0.15, x=0.3, x=0.4, x=0.5, x=0.6, x=0.7, x=0.8, х=0.9.
Разность ∆у вычисляется для тех интервалов ∆х=h, которые заключают в себе указанные точки х=0.1, 0.2,…,0.9.
Для сравнения провести еще вычисления у´ по формуле, указанной в варианте задач. Представить распечатку заряда у для х принадлежавшим участку [0;1]; у´ и I для х- [0.1;0.9].
Используемые формулы.
Метод Рунге-Кутта – метод решения дифференциального уравнения, в котором на каждом шаге xi при вычислении yi используется четыре значения углового коэффициента:
K1i=F(Xi ; Yi )=Ki;
K2i=F(Xi + H/2 ; Yi + K1i*H/2);
K3i=F(Xi + H/2 ; Yi + K2i*H/2);
K4i=F(Xi + H ; Yi + K3i*H);
KCi=(K1i + 2*K2i + 2*K3i + K4i)/6;
Yi+1=Yi + KCi*H;
Интерполирование
– восстановление всех значений функции по её отдельным узловым значениям с
помощью интерполяционного многочлена Ln(x) по
правилу: в узлах Ln(xi)=yi, вне узлов Ln(xi)![]() y(xi).
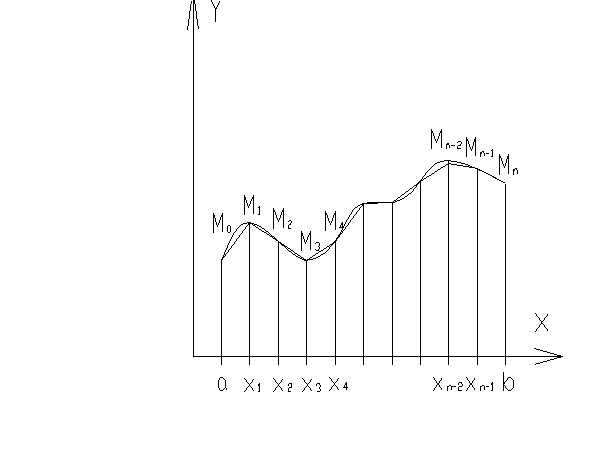
При линейной интерполяции каждые две соседние точки соединяются отрезком
прямой, уравнение которой получено с помощью интерполяционного многочлена. В
совокупности все отрезки представляют собой график интерполяционной кривой,
приближённо представляющей график искомой функции.
y(xi).
При линейной интерполяции каждые две соседние точки соединяются отрезком
прямой, уравнение которой получено с помощью интерполяционного многочлена. В
совокупности все отрезки представляют собой график интерполяционной кривой,
приближённо представляющей график искомой функции.
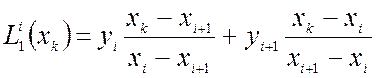
Программа:
PROGRAM вариант 8;
Uses crt,graph;
Const a=0; b=1; e=0.01;
Type mas=array [0..1000] of real;
VAR x,h,z,t,min,max:real;
i,j,m,m2,m3,ym,xm,gt,gm:integer;
l:boolean;
f1:text;
u,u1,u2,y,y1:mas;
Function F(x,y:real):real;
Begin
F:=2*x+y;
End;
function cx(x:real):integer;
begin
cx:=round(10+((x-a)/(b-a))*(xm-20));
end;
function cy(y:real):integer;
begin
cy:=round((ym-10)-((y-min)/(min+max))*(ym-20));
end;
Procedure RK(m:integer;var y:mas);
Var
K1,K2,K3,K4,KC:real;
Begin h:=(b-a)/m;
y[0]:=0.2+2*0.1+1/1000;
For i:=0 to m-1 do
Begin
K1:=F(a+i*h,y[i]);
K2:=F(a+i*h+h/2,y[i]+K1*h/2);
K3:=F(a+i*h+h/2,y[i]+K2*h/2);
K4:=F(a+i*h+h,y[i]+k3*h);
KC:=(K1+2*K2+2*K3+K4)/6;
y[i+1]:=y[i]+KC*h;
End;
End;
procedure gr(c,m:integer; h:real; var q:mas);
begin
setcolor(c);writeln (f1);
x:=a;
for i:=0 to m-1 do begin
line (cx(x),cy(q[i]),cx(x+h),cy(q[i+1]));
writeln(f1,x:7:5,' ', q[i]:7:5);
x:=x+h;
end;
writeln(f1,x:7,' ',q[m]:7:5);
end;
{nachalo osnovnoy programms}
BEGIN clrscr;
assign (f1,'results.txt');
rewrite(f1);
writeln('Method of Runge-Kutta');
writeln(f1,'Method of Runge-Kutta');
M:=5;
Repeat
RK(m,u1);
m:=2*m;
RK(m,u2);
L:=true;
m2:=m div 2;
If abs(u2[m]-u1[m2])/15>e then L:=false;
Until L;
x:=a;
u[0]:=a;
For i:=0 to m do {zabivka x}
Begin
writeln('x[',i,']=',u[i]:5:3,' ','y[',i,']=',u2[i]:5:3);
writeln(f1,'x[',i,']=',u[i]:5:3,' ','y[',i,']=',u2[i]:5:3);
x:=x+h;
u[i+1]:=x;
End;
readln;
writeln('Interpolirovanie ');
writeln(f1,'Interpolirovanie ');
x:=0;h:=0.05;
For i:=0 to 19 do {vneshnii zabivaem y}
Begin
For j:=0 to m-1 do {perebiraem massiv s x}{obrachaetsya k u u2}
Begin
If (u[j]<=x) and (x<u[j+1]) then
y[i]:=u2[j]*(x-u[j+1])/(u[j]-u[j+1])+u2[j+1]*(x-u[j])/(u[j+1]-u[j]);
End;
x:=x+h;
End;
x:=0.05;
For i:=0 to 18 do
Begin
y1[i]:=( y[i+1]-y[i])/h;
writeln('x=',x:5:3,' ','y[',i,']=',y[i]:5:3,' I=',y1[i]:6:4,' y^=',f(x,y[i]):6:4);
writeln(f1,'е=',x:5:3,' ','y[',i,']=',y[i]:5:3,' I=',y1[i]:5:3,' y^=',f(x,y[i]):6:4);
x:=x+h ;
End;
readln;
gt:=detect;
initgraph (gt,gm,'');
xm:=getmaxx;
ym:=getmaxy;
i:=10; m3:=19; h:=0.05;
repeat
line(i,5,i,ym-5);
i:=i+50;
until (i>xm-10);
i:=10;
repeat
line(5,i,xm-10,i);i:=i+50;
until(i>ym-10);
max:=y[0];
min:=y[0];
for i:=1 to m3 do begin
if (y[i] > max) then max:=y[i];
if (y[i] < min) then min:=y[i];
end;
gr(2,m3,h,y);
readln;
closegraph;
close (f1);
END.
Результаты таблицы
х=0.050 y[0]=0.401 I=0.525 y^=0.5010
х=0.100 y[1]=0.427 I=0.525 y^=0.6273
х=0.150 y[2]=0.454 I=0.791 y^=0.7535
x=0.200 y[3]=0.493 I=0.791 y^=0.8931
x=0.250 y[4]=0.533 I=1.084 y^=1.0326
x=0.300 y[5]=0.587 I=1.084 y^=1.1868
x=0.350 y[6]=0.641 I=1.409 y^=1.3410
x=0.400 y[7]=0.711 I=1.409 y^=1.5114
x=0.450 y[8]=0.782 I=1.767 y^=1.6819
x=0.500 y[9]=0.870 I=1.767 y^=1.8702
x=0.550 y[10]=0.959 I=2.163 y^=2.0586
x=0.600 y[11]=1.067 I=2.163 y^=2.2667
x=0.650 y[12]=1.175 I=2.601 y^=2.4749
x=0.700 y[13]=1.305 I=2.601 y^=2.7050
x=0.750 y[14]=1.435 I=3.085 y^=2.9350
x=0.800 y[15]=1.589 I=3.085 y^=3.1893
x=0.850 y[16]=1.744 I=3.620 y^=3.4435
x=0.900 y[17]=1.925 I=3.620 y^=3.7245
x=0.950 y[18]=2.106 I=4.211 y^=4.0055
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.