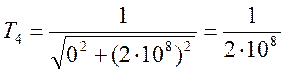 (18);
(18);
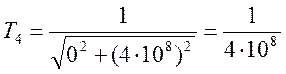 (19).
(19).
Теперь рассчитаем частоты излома:
 (20);
(20);
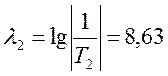 (21);
(21);
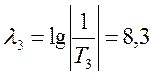 (22);
(22);
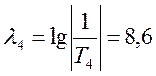 (23);
(23);
![]() (24).
(24).
По полученным точкам строим ЛАЧХ.
5 ПОСТРОЕНИЕ ЖЕЛАЕМОЙ ЛОГОРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ
Исходные данные для построения ЖЛАЧХ получаем из технического задания и технических данных устройств системы:
М=1,13; g`=0,03;
tp=0,01; g``=0,0027 – производная от g`.
E=0,0025;
По номограмме Солодовникова находим частоту среза:
tp=4p/lср (25);
следовательно: lср=4p/tp=1256 (26);
найдем координаты рабочей точки:
lк=g``/g`=0,09 (27);
A=g`/lк=0,33 (28);
A1=A/E=132 (29);
Координаты точки В: (lglк; 20lgA1).
Строим точку В и проводим через нее –20дб/дек. Ниже этой линии находится запретная зона.
Находим h и граничные частоты ЖЛАЧХ:
h=(M+1)/(M-1)=16,4 (30);
l5=lcph (31);
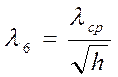 (32);
(32);
lg/l5/=3,7 (33);
lg/l6/=2,5 (34);
В результате получим типовую ЖЛАЧХ. Совместим низкочастотные части действительной и типовой и получим фактическую ЛАЧХ.
Построим ее передаточную функцию:
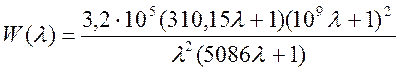 (35).
(35).
Построим ЛФЧХ системы:
f(l)=-90+arctan(T1×l)-arctan(T2×l)+2arctan(T3×l);
f(0)=-90+arctan(310,15×0) -arctan(5086×1)+arctan(109×1)=-90;
f(1)=-90+arctan(310,15×1) -arctan(5086×1)+arctan(109×1)=90;
f(10)=-90+arctan(310,15×10)-arctan(5086×10)+arctan(109×10)=90;
f(100)=-90+arctan(310,15×100)-arctan(5086×100)+arctan(109×100)=90;
f(1000)=-90+arctan(310,15×1000) -arctan(5086×1000)+arctan(109×1000)=90;
f(1000)=-90+arctan(310,15×10000) -arctan(5086×10000)+ arctan(109×10000)= =90.
Запас по фазе равен 9,42 радиан;
по амплитуде можно считать нормальным так как график ЛФЧХ не пересекает линию -2p.
6 СИНТЕЗ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
Для этого вычитаем из ФЛАЧХ график ДЛАЧХ и в результате мы получим ЛАЧХ корректирующего устройства.
Для такого типа ЛАЧХ находим соответствующую типовую схему:[2]
 |
Для этой схемы имеется следующая передаточная функция:
 |
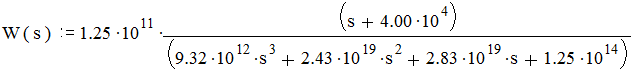
В результате получим:
В результате анализа схемы было установлено, что в системе лучше использовать программное КУ, так как в системе действуют сигналы малой амплитуды и высокой частоты. Аппаратное КУ в такой системе будет вносить слишком много помех.
7 СИНТЕЗ КОРРЕКТИРУЮЩЕЙ ПРОГРАММЫ
Для этого проведем Z – преобразование передаточной функции КУ.
В результате получим:
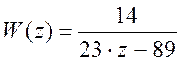 (36);
(36);
Составим разностное уравнение системы:
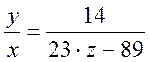 (37);
(37);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.