Найдем передаточную функцию.
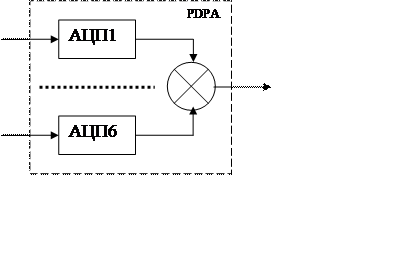 |
Рисунок 2 – Структурная схема PDPA.
Передаточная функция АЦП вычисляется так:
WАЦП=Т0 [2] (4);
где Т0 – величина обратная частоте работы процессора. Так как в системе выбран процессор с тактовой частотой 200 МГц, то передаточная функция индикаторного устройства по каждому входу будет выглядеть следующим образом:
WАЦП=1/200×106 (5).
2.3 Фильтр высокой частоты
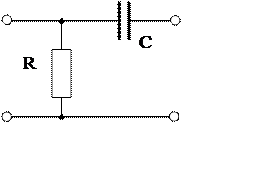 |
Рисунок 3 – Схема ФВЧ.
В этой схеме R должно иметь большое сопротивление, а С – маленькую емкость.
Для такого звена передаточная функция выглядит следующим образом:
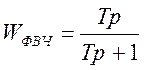 [2] (6);
[2] (6);
где Т=R×C.
Так как система работает на очень высоких частотах, то емкость конденсатора должна быть меньше 100 пФ, сопротивление резистора равняться по сути сопротивлению изоляции кабеля, т.е. быть больше 100 МОм.
Примем С=80 пФ, а R=500 МОм.
Тогда можно вычислить Т:
Т=80×10-3×500×106=40 (7);
В итоге получим следующую передаточную функцию:
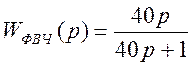 (8).
(8).
2.4 ЭВМ и сигнальное устройство
В системе ЭВМ и СУ совмещен в одном блоке, т.е. роль СУ будет выполнять периферия ЭВМ. Для системы необходима недорогая, но надежная и мощная машина. Этим требованиям удовлетворяет выбранный вариант IBM PC 200. Основой ЭВМ является процессор, а значит передаточная функция ЭВМ равна передаточной функции процессора:
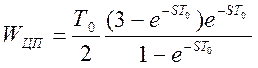 [2] (9);
[2] (9);
Подсчитав, получим:
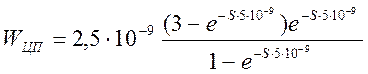 (10).
(10).
3 ПОДСЧЕТ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СИСТЕМЫ
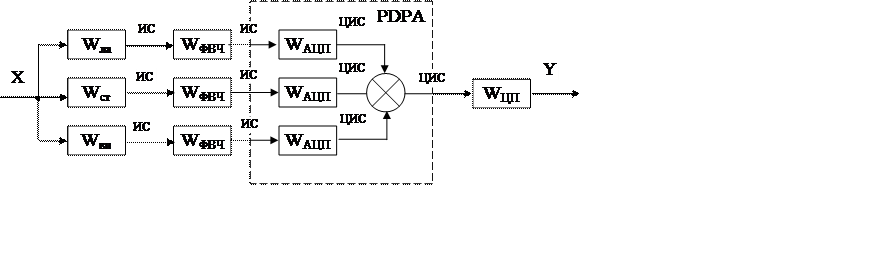 |
Рисунок 4 – Структурная схема системы.
X – входной сигнал;
ИС – информационный сигнал с датчиков;
ЦИС – оцифрованный ИС;
Y – выходной сигнал системы.
Х – входной сигнал – импульс от частичного разряда поступает на датчики. На каждом датчике учитывается соответствующая составляющая. С датчиков сигналы через ФВЧ поступают на параллельные входы АЦП устройства PDPA. С АЦП сигналы поступают на сумматор и результирующая поступает на ЦП, который вырабатывает соответствующий сигнал сигнализации у.
Передаточная функ
имеет вид:
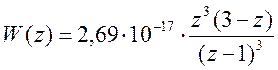 (11);
(11);
для анализа передаточной функции необходимо перейти к псевдочастоте. Для этого полученную функцию на фиксатор нуля и заменим z на (1+w)/(1-w). Получим:
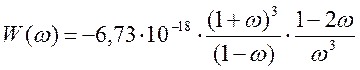 (12);
(12);
Далее заменим w на jlT0/2, получим:
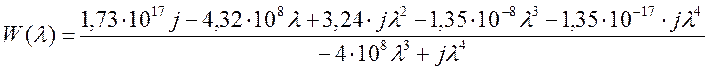 (13);
(13);
Далее проведем анализ устойчивости системы.
Для этого проведем построение АФЧХ системы.
График построен в MathCad 7:
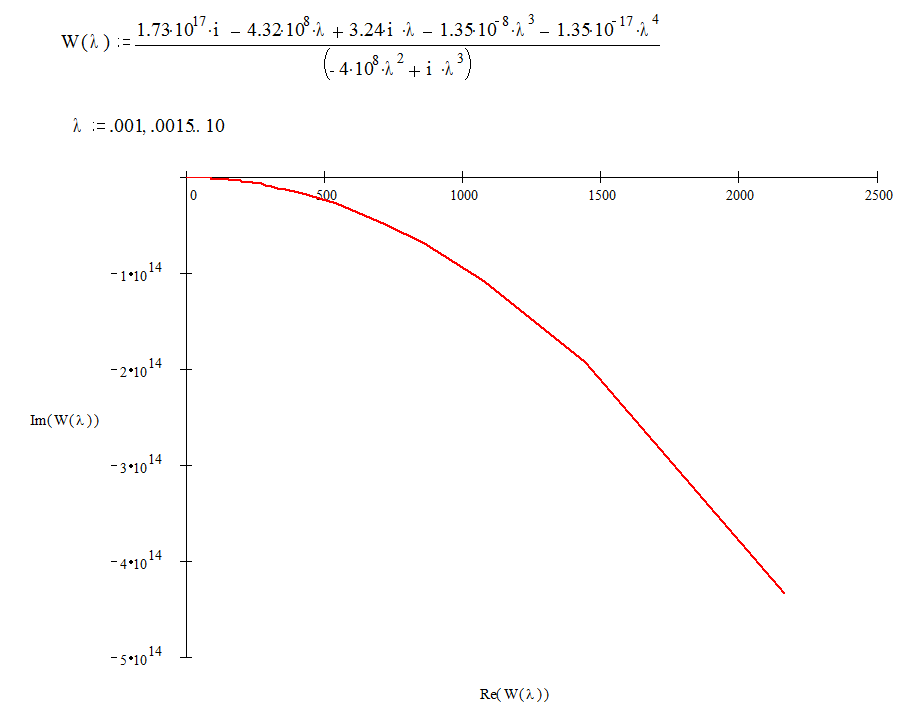 |
Так как график не огибает точку с координатами (-1;j0), то система устойчива.
4 ПОСТРОЕНИЕ ДЕЙСТВИТЕЛЬНОЙ ЛОГОРИФМИЧЕСКОЙ АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ
Для построения необходимо разбить числитель и знаменатель на скобки.
При решении числителя и знаменателя относительно l были получены следующие корни:
числитель:
l1=2,56×107+3,86×108j;
l2=-2,56×107+3,86×108j;
l3=4,29×108j;
l4=-2×108j;
знаменатель:
l1=0;
l2=0;
l3=0;
l4=-4×108j.
В результате получим:
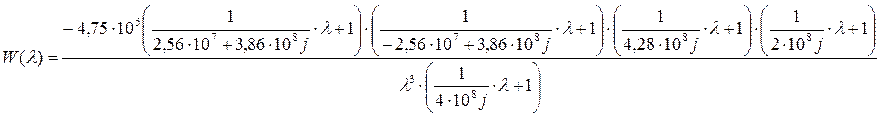 (14).
(14).
Так как под логарифм при вычислении частот излома подставляются модули 1/Т, то можно их вычислить сразу:
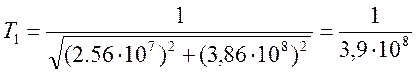 (15);
(15);
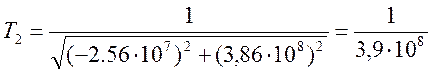 (16);
(16);
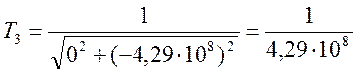 (17);
(17);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.