БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
Кафедра: УИТ
по дисциплине
Метрология.
вариант№4
гр. УИТ-31
²____²__________2008 г.
2008
Искомое сопротивление R (Ом) было измерено n раз и при этом получены результаты. Необходимо определить: среднюю квадратическую зависимость sD, интервал, в котором находиться значение измеряемого сопротивления с доверительной вероятностью Р1 и вероятную погрешность результата измерения eD для доверительной вероятности Р2.
Дано: Р1 = 0,98; Р2 = 0,8.
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ri, Ом |
545,6 |
510,3 |
530,3 |
527,7 |
543,8 |
539,2 |
537,1 |
544,4 |
|
I |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Ri, Ом |
548,3 |
550,4 |
545,5 |
537,6 |
512,3 |
540,9 |
547,7 |
Найти: R, s, em.
Решение:
Так как n ³ 15, то воспользуемся алгоритмом обработки данных при большом числе измерений.
1)
Rср = 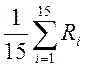 =
= ![]() 8067,1
= 537,8 (Ом);
8067,1
= 537,8 (Ом);
2) Определяем абсолютную погрешность Di = Ri - Rср;
D1 = 7,8; D2 = -27,5; D3 = -7,5; D4 = -10,1; D5 = 6; D6 = 1,4; D7 = -0,7; D8 = 6,6; D9 = 10,5; D10 = 12,6; D11 = 7,7; D12 = -0,2; D13 = -25,5; D14 = 3,2; D15 = 9,9.
3)
Так как ![]() Di
¹ 0, то мы имеем дело с распределением Стьюдента.
Di
¹ 0, то мы имеем дело с распределением Стьюдента.
4)
s = 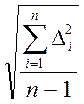 =
= 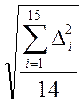 =
= 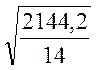 =12,3757;
=12,3757;
5)
sx
= 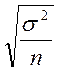 =
= ![]() =
= 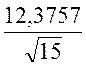 = 3,1954;
= 3,1954;
6) Dmax = 3sx = 9,5862;
7) Выявляем промахи, если Di ³ Dmax , i: 2,4,9,10,13,15.
Остается:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ri,Ом |
545,6 |
530,3 |
543,8 |
539,2 |
537,1 |
544,4 |
545,5 |
537,6 |
547,7 |
Rср = 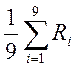 = 541,24;
= 541,24;
D1 = -4,36; D2 = 10,94; D3 = -2,56; D4 = 2,04; D5 = 4,14; D6 = -3,16; D7 = -4,26; D8 = 3,64; D9 = -6,46.
Так как ![]() Di ¹ 0, то мы
имеем дело с распределением Стьюдента.
Di ¹ 0, то мы
имеем дело с распределением Стьюдента.
s = 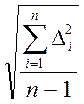 =
= 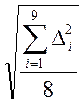 = 5,5864;
= 5,5864;
sx
= 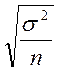 =
= ![]() =
1,8621;
=
1,8621;
8) Находим границы доверительного интервала D1.
По таблице распределения Стьюдента при Р1 = 0,98,t1 = 2,5, Р2 = 0,8, t2 = 1,3;
8) Определим интервал: D1 = t1sх = 4,65525;
D2 = t2sx = 2,42073;
R = Rср ± D1 = 541,24 ± 4,65525;
em
= ![]() 100% = 0,45%.
100% = 0,45%.
Ответ: s = 5,5864; R = 541,24 ± 4,65525 Ом; em = 0,45%.
Определить наиболее достоверное значение напряжения постоянного тока, измеренного компенсатором постоянного тока, среднеквадратичную погрешность ряда измерений sU, среднеквадратичную погрешность среднеарифметического sср, доверительный интервал (при заданной доверительной вероятности Р) и предельную погрешность найденного значения UСР.
Дано: Р = 0,95.
|
i |
1 |
2 |
3 |
4 |
5 |
|
U1,В |
120,03 |
120,05 |
120,01 |
119,98 |
119,93 |
|
i |
6 |
7 |
8 |
9 |
10 |
|
U1,В |
120,15 |
120,20 |
119,95 |
119,94 |
120,11 |
Найти: Uср,s, sх, U, em.
Решение:
Так как n < 15, то воспользуемся алгоритмом обработки результатов при малом числе измерений.
1)
Uср = 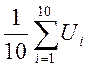 = 120,035;
= 120,035;
2) Di = Uср - Ui;
D1 = 0,005; D2 = -0,015; D3 = 0,025; D4 = 0,055; D5 = 0,105; D6 = -0,115; D7 = -0,165; D8 = 0,085; D9 = 0,095; D10 = -0,075.
3)
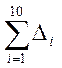 ¹0, значит мы имееи дело с распределением Стьюдента.
¹0, значит мы имееи дело с распределением Стьюдента.
4)
s = 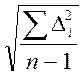 = 0,09265; sx =
= 0,09265; sx = ![]() = 0,0293;
= 0,0293;
5) Dmax = 3sx = 0,0879;
6) Выявляем промахи, если Di ³ Dmax: i = 5, 6,7,9.
Остается:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
U1,В |
120,03 |
120,05 |
120,01 |
119,98 |
119,95 |
120,11 |
7)
а) Uср = 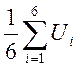 = 120,02;
= 120,02;
б) D1 = -0,01; D2 = -0,03; D3 = 0,01; D4 = 0,04; D5 = 0,07; D6 = -0,09;
в)
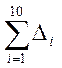 ¹0, значит мы имееи
дело с распределением Стьюдента.
¹0, значит мы имееи
дело с распределением Стьюдента.
г)
s = 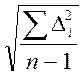 =0,056; sx =
=0,056; sx = ![]() = 0,0229;
= 0,0229;
8) Находим границы доверительного интервала D1.
По таблице распределения Стьюдента при Р = 0,95 и n = 6 находим t6 = 2,57, тогда D1 = t6sx = 0,063;
U= Uср ± D1 = 120,02 ± 0,063;
em
= ![]() 100% = 0,05%.
100% = 0,05%.
Ответ: наиболее достоверное значение напряжения Uср = 120,02В;
среднеквадратичная погрешность измерения s = 0,056;
погрешность от среднего арифметического sх = 0,0229;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.