Идентификация. Методы идентификации и диагностики, страница 2

Зад-чи РА: устан формы завис между переменными, оценка функции регрессии, оценка неизвестных значений зависимой переменной (прогноз). РА вкл 2 осн компоненты:  1) оценка вектора коэф-ов с помощью метода наименьших квадратов:    по МНК; 2) ДА для оценки адекватности ММ. Для проведения РА надо: 1)кол-во экс-ов >= 30; 2)распределение вых в-ны норм; 3); 4)X детерменирована; 5); 6) > времени затухания АФ; 7)учет динамики в виде транспортного запаздывания, кот опр как время нахождения максимума ВАФ.

МНК (для построения ед прямой с мин ошибкой ): 1) 2) расчетная вых в-на 3) проводим экс-т (>30), x_i и y_iсводим в табл; 4) строим график, опр вид регрессии (-/+, лин/не-); 5) По ф-ле лин регрессии находим расч вы­х в-ны: 6) находим сумму квадратов отклонений: 7) рассч 95% ошибку аппроксимации: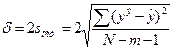  

Нелинейная регрессия - > сложная односторонняя стохастич связь. Виды:1)степенная; 2)логарифмич; 3) экспоненц; 4)полиноминальн; 5) гиперболич. Ход работы: 1) ввести данные из табл; 2) постр гр; 3) по гр с пом линии тренда опр вид нелин регр с исп коэф опр-ти R²; 4) вывести У линии; 5) линеаризация получ У (м-ом логарифмирования); 6) У_расч рассч по лин-ому У; 7) линеаризовать У_экс (пролог-ть); 8) найти кв отклон У_расч, У_экс; 9)   10) 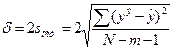 - цель работы 11) постр гр У_расч и Y^*(лин-ое эксп-ое).  

Задача ДА - опр той ч эксперим данных,  кот опис-ся регр моделью (опр коэф детерминации R² ), а также опр адекватности регрессионной модели по F критерию.  Для этого исп осн У ДА: , где 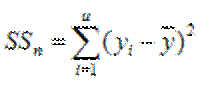- полная сумма квадратичотклонений (хар-ет разброс значений вых в-ны y вокруг его ср знач ;  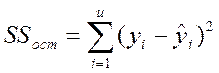- остаточная сумма отклонений (исп в качестве критерия МНК); 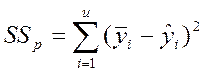- сумма квадратичотклонений расчетных значений вых в-ны   от ср знач  . Коэф детерминации R²: 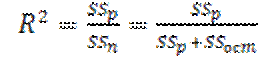 ,  Чем ближе R²к 1, тем точнее регр модель. При малых объемах выборки (N<30) исп коэф множественной корреляции R: 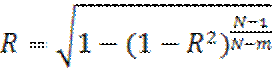 ,  где N – кол-во выборки; m – кол-во входов.  Для оценки адекватности регр модели исп критерий Фишера: 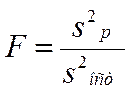 Дисперсия, обусл регрессией- 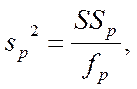 где  f_р- число степеней свободы: . Остаточная дисперсия: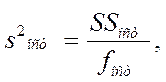 где  f_ост- число степеней свободы ост суммы:  , где N- число эксп-ов, m – кол-во входов. Для опр адекватности регр модели F_расч и  Если , то при соотв уровне значимости регр модель адекватна.

Результаты ДА сводятся в табл:

	f	SS	MS	F
регрессия
остатки
Итого

SS - сумма квадратов; f- число степеней свободы; MS - ср квадрат отклонений (дисперсия); F- расчетное значение отношения Фишера. Если регр модель адекватна, опр значимость коэф регрессии: анализ отнош коэф регр и его СКО ( распр Стьюдента, t – критерий):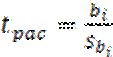  и сравн его с табл знач t – критерия, кот опр степенью свободы и зад вероятностью Р : t_таб (, Р). Если t_рас>t_таб, то коэф b_iявлзначимым. Тогда доверит интервал:  Если коэф регр незначим, то соотв ему вх фактор несущественно влияет на вых в-ну и его можно исключ из регрмодели.

КА: 1) проведем выборки; 2) на осн кажд выборки проведём оценку  ср значения Д  всех компонентов анализа; 3) приведём все переменные к станд виду; 4) запишем У регрессии станд переменных:   5) по критерию МНК ост сумма сводится к мин:  6) для опр коэф-ов найдём частные производные и сост У Гаусса: 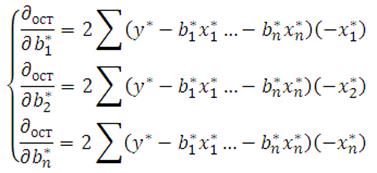 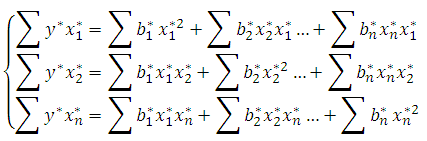 7) умножаем левую и правую ч У из системы на (1/n), получим 2ой смешанный момент и коэф вз корреляции: 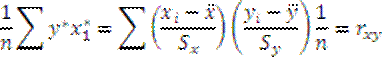,  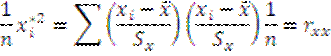8) тогда сист принимает вид: 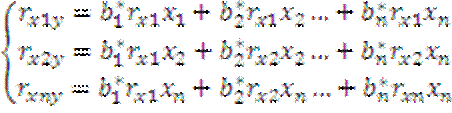  9) введем вектор вз корреляции и матрицу: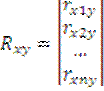

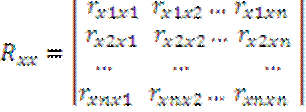
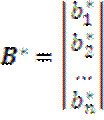   10) значит R_xy=R_xxB*, B*=R_xy/R_xx,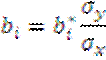     

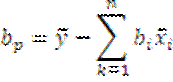
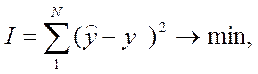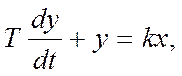
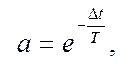
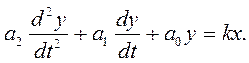
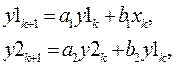
МЕТОД НЕЛИН ПР-ИЯ: задача – подобрать такой вектор параметров модели B, чтобы при выбр  У ММ О: Апериодич звено 1 п-ка:   Апериодич звено 2 п-ка:   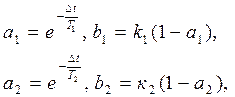Реал интегрир звено: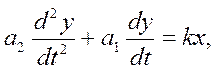 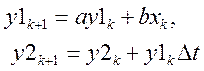   1) созд табл и ввести исходные данные; 2) постр гр зависим; 3) по виду гр выбр вид модели (тип звена) и запис его ПФ; 4) по гр приблизительно рассч пар-ры звена, вых пер-ную; 5) используя алгоритм нелинейного пр-ия  Excel «По­иск решения», найти параметры модели, дающие мин значе­ние критерия, и получить итоговые У для звеньев.

З-чи диагностики: 1)проверка исправности (вкл О после хранения/ремонта, введение в эксп-ию); 2) проверка работоспособности (вкл сист в А, профилактич осмотрах, огранич t проверки); 3) проверка правильности ф-ия (чтобы не привод к опасн послед для ОУ); 4) поиск неисправностей (эквив неиспр-ти, глубина поиска).

Кл-ия тестов техн диагноза: I по назнач: 1) проверочные (проверка испр-ти, раб-ти); 2) диагностич (с указ места неиспр-ти – поиск неиспр-ти). II по полноте обнаруж неиспр-тей: 1) одиночный; 2) кратный; 3) полный (на стадии изготовления). III по длине: 1) тривиальные (макс); 2) минимизированные; 3) минимальные (> вычислений).

Ф-ии СКД: 1) измер Д-ого пар-ра; 2) сравнение с нормой и опр отклонений от нее; 3) опр причины и места отклон; 4) формир реш по рез-ам ан-за. Сост из технолог и матем обеспеч.

Диагн модель – сов выбр м-ов построения и ан-за ММ, опр спец-ку алг-ма и сп-ов Д-ия. Бывают: явные и не-; непрер, дискр, гибридн, спец. М-ды представлен вз-зей м-ду сост ОД: 1) аналит: соотноше м-ду сост ОД, Д-ыми пар-ми, показ-ми кач-ва в аналит виде; 2) графо-аналит: своеобр диа-ма, отраж процессы и свзяи в ОД; 3) функц-логич: на осн логич ан-за ф-ия ОД; 4) информац: инф-ое опис-ие сист и проц контроля. ММ по глубине опис: лин и не-, детермин и стохастич, с распр пар-ми.

Синтез логич модели тестирования: 1) в сист выдел отд функц эл-ты с доступными для измер вх и вых; 2) для кажд эл-та указ диап-н доп вх/вых пар-ов; 3) функц сх с выдел эл-ми и связями; 4) возм сост сист; 5) ТФН.