

Индивидуальное задание №2
Обозначения: ![]() – номер группы. Например, для групп
МТ-291, МТ-292, МТ-191, МТ-192, соответствующие номера групп будут равны 21,
22, 11, 12. То есть, вторая цифра - год поступления - опускается. Через
– номер группы. Например, для групп
МТ-291, МТ-292, МТ-191, МТ-192, соответствующие номера групп будут равны 21,
22, 11, 12. То есть, вторая цифра - год поступления - опускается. Через ![]() обозначается номер студента в списке
группы.
обозначается номер студента в списке
группы.
Все данные приведены в брошюре В.Ф. Пожидаев «Прикладные задачи математической статистики», Луганск, издательство ВУГУ, 1998.
1. Дискретная случайная величина ![]() принимает
два значения:
принимает
два значения: ![]() и
и ![]() с
вероятностями
с
вероятностями ![]() .и
.и ![]() (
(![]() ). При этом
). При этом ![]() . По
условию задачи даны числовые значения
. По
условию задачи даны числовые значения ![]() ,
, ![]() , и
, и ![]() .
Требуется найти значения
.
Требуется найти значения ![]() и
и ![]() . Для каждого варианта значения
. Для каждого варианта значения ![]() и
и ![]() определяются
выражениями:
определяются
выражениями:
![]() ,
, ![]() ,
, ![]() .
.
2. В рамках предыдущей задачи даны ![]() ,
, ![]() и
и ![]() . Требуется
найти
. Требуется
найти ![]() и
и ![]() . При
этом для каждого варианта исходные данные задаются формулами:
. При
этом для каждого варианта исходные данные задаются формулами:
![]() ,
, ![]() ,
, ![]() .
.
3. Случайная величина ![]() равномерно распределена
в интервале
равномерно распределена
в интервале ![]() , границы которого неизвестны. Найти эти
границы, если математическое ожидание и дисперсия заданы. При этом для каждого
варианта:
, границы которого неизвестны. Найти эти
границы, если математическое ожидание и дисперсия заданы. При этом для каждого
варианта:
![]() ,
, ![]() .
.
4. По двум значениям функции распределения ![]() и
и ![]() в точках
в точках ![]() и
и ![]() нормально распределенной случайной
величины требуется найти ее математическое ожидание и дисперсию. При этом для
каждого варианта:
нормально распределенной случайной
величины требуется найти ее математическое ожидание и дисперсию. При этом для
каждого варианта:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5. Треугольное распределение (распределение Симпсона) задано на отрезке ![]() . Найти математическое ожидание
. Найти математическое ожидание ![]() , дисперсию
, дисперсию ![]() , асимметрию
, асимметрию
![]() и эксцесс
и эксцесс ![]() , если
границы интервала для каждого варианта равны:
, если
границы интервала для каждого варианта равны:
![]() ,
, ![]() .
.
6.
Случайная величина ![]() подчиняется логарифмически нормальному
закону
подчиняется логарифмически нормальному
закону 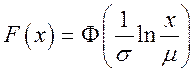 с параметрами
с параметрами ![]() и
и ![]() , задаваемыми по правилам:
, задаваемыми по правилам: ![]() ,
, ![]() . Найти математическое
ожидание
. Найти математическое
ожидание ![]() и вероятность попадания в интервал
и вероятность попадания в интервал ![]() , границы которого задаются равенствами:
, границы которого задаются равенствами: ![]() ,
, ![]() .
.
7.
Вероятность того, что каждый из
30000 исследованных образцов минерала обладает признаком ![]() , равна
, равна ![]() . Найти
границу отклонения частоты появления признака
. Найти
границу отклонения частоты появления признака ![]() от его
вероятности по абсолютной величине, если это отклонение можно ожидать с
вероятностью, не меньшей
от его
вероятности по абсолютной величине, если это отклонение можно ожидать с
вероятностью, не меньшей ![]() , причем
, причем ![]() .
.
8.
Случайная величина ![]() описывается законом Релея
описывается законом Релея 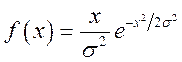 ,
, ![]() . Дано:
. Дано:
![]() .
.
Найти:
математическое ожидание ![]() , дисперсию
, дисперсию ![]() , асимметрию
, асимметрию ![]() и
эксцесс
и
эксцесс ![]()
9. Закон распределения случайной величины -![]() экспоненциальный
экспоненциальный ![]() ,
,
![]() .
.
Дано: 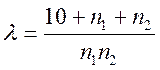 .
Найти: математическое ожидание
.
Найти: математическое ожидание ![]() , дисперсию
, дисперсию ![]() , третий
, третий ![]() и
четвертый
и
четвертый ![]() центральный моменты, асимметрию
центральный моменты, асимметрию ![]() и эксцесс
и эксцесс ![]() .
.
10. Случайная величина ![]() распределена
по закону Вейбула
распределена
по закону Вейбула ![]() . По заданным значениям
. По заданным значениям ![]() ,
, ![]() и
и ![]() ,
, ![]() требуется
найти параметры
требуется
найти параметры ![]() и
и ![]() закона
распределения, а также вычислить математическое ожидание
закона
распределения, а также вычислить математическое ожидание ![]() .
.
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
11.
Случайная величина ![]() описывается законом Эрланга
описывается законом Эрланга
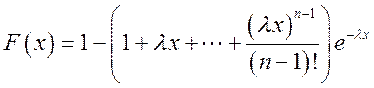 .
.
Дано:
![]() ,
, 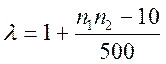 ,
, 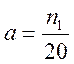 ,
, 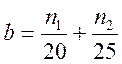 .
.
Найти:
математическое ожидание ![]() и вероятность
и вероятность ![]() .
.
12. В законе распределения Парето ![]() при
при
![]() и
и ![]() при
при ![]() по условию заданы:
по условию заданы:
![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Найти:
константу ![]() , математическое ожидание
, математическое ожидание ![]() , дисперсию
, дисперсию ![]() и вероятность
попадания
и вероятность
попадания ![]() случайной величины
случайной величины ![]() в
интервал
в
интервал ![]() .
.
13. Случайная величина ![]() равномерно
распределена на отрезке (-1,+1). Построить закон распределения случайной
величины
равномерно
распределена на отрезке (-1,+1). Построить закон распределения случайной
величины ![]() , при
, при ![]() и
и ![]() при
при ![]() . Найти
ее математическое ожидание
. Найти
ее математическое ожидание ![]() , дисперсию
, дисперсию ![]() , третий
, третий ![]() и
четвертый
и
четвертый ![]() центральный моменты, асимметрию
центральный моменты, асимметрию ![]() и эксцесс
и эксцесс ![]() .
.
14.
Случайный вектор ![]() задан
распределением:
задан
распределением:
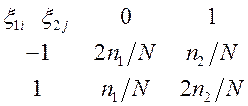 ,
,
где
![]() . Вектор
. Вектор ![]() задан
своими компонентами:
задан
своими компонентами: ![]() ,
, ![]() . Найти
матрицу ковариации вектора
. Найти
матрицу ковариации вектора ![]() . Будут ли случайные
величины
. Будут ли случайные
величины ![]() и
и ![]() независимыми?
независимыми?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.