Отже, якщо функція ![]() визначена на спектрі
матриці A, те:
визначена на спектрі
матриці A, те:
f(A) = g(A),
де ![]() -
будь-який многочлен, що приймає того ж значення на спектрі матриці A, що й
-
будь-який многочлен, що приймає того ж значення на спектрі матриці A, що й ![]() ,
тобто:
,
тобто:
![]()
Серед всіх многочленів з комплексними коефіцієнтами, що приймає ті ж
значення, що й ![]() , є лише один многочлен
, є лише один многочлен ![]() степеня менше m. Цей многочлен однозначно
визначається інтерполяційними умовами:
степеня менше m. Цей многочлен однозначно
визначається інтерполяційними умовами:
![]()
![]() (k = 1,2,…,u) (2...51)
(k = 1,2,…,u) (2...51)
Многочлен r(l) називають інтерполяційним многочленом Лагранжа-Сильвестра для функції f(l) на спектрі матриці A. Його побудову в загальному випадку відомо. В окремому випадку, коли характеристичний і мінімальний многочлени мають лише одне характеристичне число (u = 1), тобто:
![]()
інтерполяційний многочлен
Лагранжа-Сильвестра дорівнює сумі m членів розкладання Тейлора по степенях ![]() для функції f(l):
для функції f(l):
 (2.52)
(2.52)
Отже, можна сформулювати визначення для функції матричного аргументу, скориставшись поняттям інтерполяційного многочлена:
Якщо ![]() - функція, визначена на спектрі матриці A,
a
- функція, визначена на спектрі матриці A,
a ![]() - відповідний інтерполяційний многочлен
Лагранжа-Сильвестра, то:
- відповідний інтерполяційний многочлен
Лагранжа-Сильвестра, то:
![]() (2.53)
(2.53)
Приклад 15. Для функції ![]() побудувати функцію матричного
аргументу f(A), якщо:
побудувати функцію матричного
аргументу f(A), якщо:

Розв’язання. Мінімальний многочлен для матриці A має вигляд ![]() . Тому значеннями функції f(l) на спектрі матриці A
будуть числа
. Тому значеннями функції f(l) на спектрі матриці A
будуть числа ![]() а це значить, що інтерполяційний
многочлен Лагранжа-Сильвестра має вигляд:
а це значить, що інтерполяційний
многочлен Лагранжа-Сильвестра має вигляд:
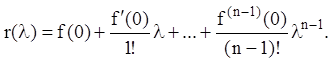
Отже, з огляду на (2.53), одержуємо:
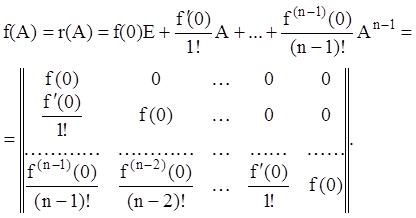 (2.54)
(2.54)
Приклад 16. Для функції f(l) побудувати функцію матричного аргументу f(J), якщо 
Очевидно, що ![]() тому
тому ![]() З
формули (2.48) треба, що мінімальний многочлен для матриці J має вигляд:
З
формули (2.48) треба, що мінімальний многочлен для матриці J має вигляд:
![]()
Тоді інтерполяційний многочлен ![]() для
функції
для
функції ![]() визначиться рівністю
визначиться рівністю
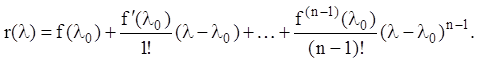
Тоді, з огляду на (2.54), одержуємо:
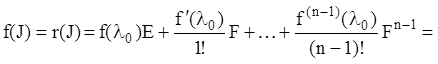
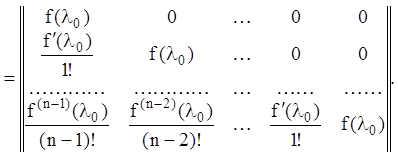 (2.55)
(2.55)
У загальному випадку інтерполяційний многочлен Лагранжа-Сильвестра ![]() можна визначити з тотожності
Лагранжа-Сильвестра:
можна визначити з тотожності
Лагранжа-Сильвестра:
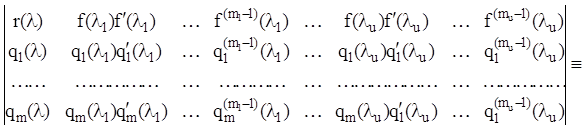 0 (2.56),
0 (2.56),
де
![]() – лінійно незалежні многочлени ступеня не
вище
– лінійно незалежні многочлени ступеня не
вище ![]() (j = 1,2,…,u)... При цьому
(j = 1,2,…,u)... При цьому ![]() де
де ![]() –
кратність характеристичного числа в мінімальному многочлені;
–
кратність характеристичного числа в мінімальному многочлені;![]() тут n і
тут n і ![]() відповідно
розмірність і ранг матриці
відповідно
розмірність і ранг матриці ![]()
Приклад 17. Для функції f(l) побудувати функцію матричного аргументу f(A), якщо 
Розв’язання. Характеристичний многочлен матриці A має вигляд:
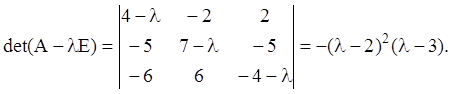
Тоді ![]() є характеристичним (власним) числом матриці
A кратності
є характеристичним (власним) числом матриці
A кратності ![]() й
й ![]() –
кратності
–
кратності ![]() . Для першого власного числа
. Для першого власного числа ![]()
![]() , де
, де ![]() – ранг матриці:
– ранг матриці:
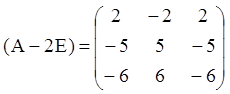
рівний ![]() Тоді
Тоді ![]() й
й ![]() (тут
(тут ![]() –
кратність характеристичного числа). Для
–
кратність характеристичного числа). Для ![]() знаходимо
знаходимо
![]()
Мінімальний многочлен матриці A має вигляд:
![]()
Як система ![]() вибираємо многочлени l – 2 й l – 3.
вибираємо многочлени l – 2 й l – 3.
Тогда по формулі (2.56) одержуємо:
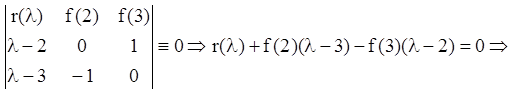
![]()
Тоді ![]() або
або 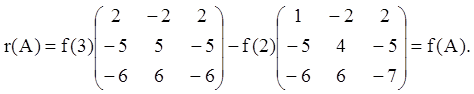
Перелічимо деякі властивості функцій від матриць, що становлять інтерес для лінійних систем диференціальних рівнянь.
1. Якщо A - квазідіагональна матриця
![]() (2.57)
(2.57)
то ![]()
2. Якщо дві матриці A й B подібні й матриці U перетворить A в B, тобто
![]()
то матриці f(A) і f(B) подібні, і та ж матриця U перетворить f(A) в f(B), тобто
![]() (2.58)
(2.58)
3. Якщо ![]() – характеристичні числа матриці
A n-го порядку, то
– характеристичні числа матриці
A n-го порядку, то ![]() – система характеристичних чисел
матриці f(A).
– система характеристичних чисел
матриці f(A).
Тому що довільна матриця ![]() n-го порядку завжди
приводиться перетворенням подоби до нормального жорданової формі J
n-го порядку завжди
приводиться перетворенням подоби до нормального жорданової формі J
![]()
то відповідно до властивості 2 для функцій матричного аргументу, завжди має:
![]()
Остання рівність у розгорнутому виді записується:
![]() (2.59)
(2.59)
Приклад 18. Нехай задана деяка квадратна матриця J n-го порядку в нормальної жорданової формі:

У недіагональних блоках всі її елементи дорівнюють нулю. Знайдемо f(J).Відповідно до формул (2.55), (2.57) одержуємо:

Дамо останній матриці номер (2.60).
Тут, як й у матриці J, всі елементи в недіагональних блоках дорівнюють нулю.
Розглянемо як функція ![]() експонентну функцію
скалярного аргументу:
експонентну функцію
скалярного аргументу:
 .
(2.61)
.
(2.61)
Нехай мінімальний многочлен постійної матриці A має вигляд (2.48), де ![]() – всі різні характеристичні числа матриці
A. Тоді m чисел (2.50)
– всі різні характеристичні числа матриці
A. Тоді m чисел (2.50) 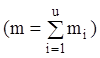 для функції
для функції ![]() мають сенс і визначають значення
експонентної функції
мають сенс і визначають значення
експонентної функції ![]() на спектрі матриці A для всіх кінцевих
характеристичних чисел
на спектрі матриці A для всіх кінцевих
характеристичних чисел ![]() (j = 1,2,…,u)... Отже, для всіх
кінцевих матриць (матриць із кінцевими елементами) експонентна функція
матричного аргументу має сенс і відповідно, згідно (2.60), визначається
матричним статечним рядом:
(j = 1,2,…,u)... Отже, для всіх
кінцевих матриць (матриць із кінцевими елементами) експонентна функція
матричного аргументу має сенс і відповідно, згідно (2.60), визначається
матричним статечним рядом:
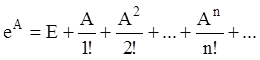 , (2.62)
, (2.62)
збіжної для будь-якої кінцевої матриці A, а його сумою є експонентна функція матриці A.
Якщо замість постійної матриці A розглянути матрицю:
 (2.63)
(2.63)
елементи якої ![]() є обмеженими функціями на розглянутому
інтервалі зміни t, те:
є обмеженими функціями на розглянутому
інтервалі зміни t, те:
 .
(2.64)
.
(2.64)
Нехай матриця Z(t) диференціювана матриця, і Z комутирує зі своїй
похідній ![]() (2.13). Тоді з (2.63) з урахуванням
(2.14), формальним диференціюванням знаходимо матричний ряд для похідної:
(2.13). Тоді з (2.63) з урахуванням
(2.14), формальним диференціюванням знаходимо матричний ряд для похідної:
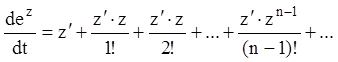 ;
;
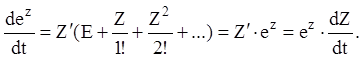 (2.65)
(2.65)
Зокрема, якщо Z(t) = At , де A - постійна матриця, тобто:
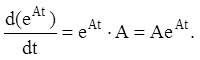 (2.66)
(2.66)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.