Визначення випадкового процесу. Приклади. Класифікація процесів. Аналіз тимчасових рядів. Критерії випадковості. Поворотні крапки, страница 2

Тимчасові ряди розрізняються по своїй природі. Одні перемінний, складовий тимчасовий ряд існують у кожен момент часу і можуть розглядатися як існуючі безупинно. Наприклад, температура  в заданому місці, ціна даного товару на відкритому ринку або положення снаряда в польоті. Інші утворяться тільки шляхом підсумовування (агрегирования) за визначений період. Наприклад, кількість опадів, випуск промислової продукції, відстань, пройдена авіалайнером. Треті у свою чергу існують (або починають існувати) тільки в окремі інтервали часу: врожай тієї або іншої культури в гарячу пору, число голосів політичної партії на загальних виборах, платежі, що підлягають сплаті наприкінці кварталів. Іноді в нас немає можливості вибору моментів часу, коли робити спостереження, наприклад при визначенні врожаїв у жнива. В інших випадках визначений вибір можливий, але без обмежень. Наприклад, дані про імпорт представляються звичайно по місяцях і тільки як виняток урядове агентство дає цифри за більш короткі інтервали або дробові періоди. У граничних випадках ряди можна спос

терігати майже нескінченно або у всякому разі, настільки довго, наскільки вистачить нашого терпіння і сил. Відомими прикладами можуть служити запису на обертовому барабані температури і барометричного тиску або альфа-ритмів головного мозку на энцефалографе.

Огляд уже приведених прикладів тимчасових рядів і багатьох інших рядів наводить на думку, що корисно в загальному випадку розглядати ряд як суміш чотирьох компонентів:

(а) тренда або довгострокового руху;

(б) більш-менш регулярних коливань щодо тренда;

(в) сезонного компонента;

(г) залишку або несистематичного випадкового ефекту.

Ряд зручно представляти у виді суми цих чотирьох компонентів, і однієї з цілей аналізу є розкладання ряду на його складові для окремого вивчення. Однак варто пам'ятати, що, надходячи так, ми фактично постулируем модель. Можливо, доцільно припустити, що тренд порозумівається наявністю постійних сил, що одноманітно діють приблизно в тому самому напрямку, а короткострокові коливання щодо цього довгострокового руху відбуваються по сукупності причин, і що в обох рухах якесь збурювання, властивим випадковим подіям і зумовлююча поява залишку. Але те, що це так і що ефекти від різних сил аддитивны, є припущенням і має характер гіпотези, від якої ми завжди повинні бути готові відмовитися, якщо наша модель погано відповідає даним.

Для більш глибокого вивчення проблем тимчасових рядів можна порекомендувати наступні монографії: М.Кендэл «Тимчасові ряди», Д. Конс, П. Льюис «Статистичний аналіз послідовностей подій», Дж. Бонс, Г. Дженкинс «Аналіз тимчасових рядів».

4.   Критерії випадковості

Найпростішою гіпотезою, яку можна висунути щодо коливного ряду, є припущення, що коливання випадкові. На практиці буває досить лише подивитися на дані, щоб відкинути цю гіпотезу, але в деяких випадках необхідні більш точні критерії, наприклад при дослідженні даних про ячмінь або при вивченні залишків, отриманих вирахуванням з вихідного ряду систематичних елементів, коли потрібно установити, чи не залишилося в них якої-небудь систематизації.

У випадкових рядах, відповідно до гіпотези, спостереження незалежні і можуть випливати в будь-якому порядку. Можливе застосування необмеженого числа критеріїв випадковості, але одні критерії по визначених розуміннях краще, ніж інші.

(а) Бажано щоб критерій не вимагав яких-небудь обмежень на вид розподілу сукупності, з якої, по припущенню, витягаються спостережені значення.

(б) Необхідні обчислення повинні бути зведені до мінімуму.

(в) Обчислення повинні легко обновлятися; іншими словами, необхідно, щоб не було потрібно проводити всі обчислення із самого початку, якщо після підрахунку критерію з часом додаються нові спостереження.

Вибір критерію до деякої міри залежить від того, які висуваються альтернативні гіпотези. Робота Неймана і Пірса по перевірці гіпотез підтверджує, що ніхто не перевіряє гіпотезу саму по собі, а лише в порівнянні з іншими можливими гіпотезами. Не завжди легко точно визначити, які альтернативні гіпотези, доцільно висунути, але звичайно маються деякі розуміння, що можуть у значній мірі допомогти при виборі критерію. Наприклад, у випадку, коли дані по виду начебто мають тренд, потрібен критерій, відмінний від того, котрий використовується при підозрі на періодичність.

5.  Поворотні крапки

Найбільш простий для застосування критерій, особливо якщо ряд зображений графічно, складається в підрахунку піків і западин. «Пік» — це величина, що більше двох сусідніх. «Западина», навпаки, — значення, що менше двох сусідніх. Обоє ці значення називаються «поворотними крапками» і нам має бути розглянути питання: яке розподіл числа поворотних крапок у випадковому ряді?

Розглянемо кінцевий ряд з  величин . Початкове значення не можна вважати поворотною крапкою, тому що  невідомо; і аналогічно, не можна розглядати як поворотну крапку останнє значення, тому що невідомо . Для визначення поворотної крапки потрібні три послідовних значення. Якщо ряд случає, то ці три значення можуть випливати в кожнім із шести можливих порядків з рівною імовірністю. Тільки в чотирьох з них буде поворотна крапка, а саме коли найбільших або найменше з трьох значень знаходиться в середині. Отже, імовірність виявлення поворотної крапки в будь-якій групі з трьох значень дорівнює .

Для групи з  величин визначимо «рахункову» перемінну  як

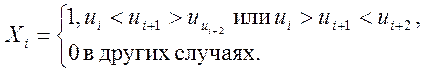
Тоді число поворотних крапок  у ряді є просто

,

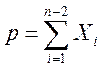і відразу ж одержуємо

.

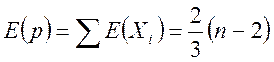Це очікуване число поворотних крапок (іншими словами, поворотна крапка приходиться на кожні  спостереження). Якщо їх більше (рідкий випадок), то ряд є швидко коливним, і це не може бути пояснено тільки випадковістю. Якщо ж їх менше, те послідовні значення позитивно коррелированы. (Однак для того, щоб зробити висновок, чи істотний різниця між спостереженим і очікуваним числом, бажано обчислити дисперсію).

Існують також рангові критерії випадковості і критерії знаків разностей.