Механика системы микрочастиц, страница 3

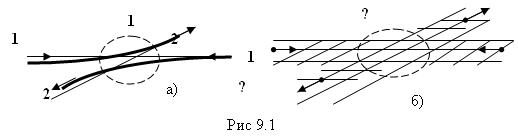
Принцип тождественности связан и с тем, что при тесном сближении невозможно проследить за каждой частицей в отдельности вследствие неопределенности положений частиц в пространстве. В случае столкновения классических тел всегда можно установить, какое из них отскочило вверх или вниз (рис.9.1.а). Для квантовых объектов вместо траекторий приходится рассматривать «трубку», в которой движется волновой пакет (рис.9.1.б) Если нет перекрывания волновых пакетов, то частицы можно различить по их положению в пространстве.

Однако при взаимодействии или даже при сближении без взаимодействия трубки пересекаются и нельзя установить, где какая частица находится. Поэтому после соударения можно сказать только, что одна из частиц полетела вверх, а другая – вниз. В микроскопической системе, например, в атоме, волновые функции отдельных частиц (электронов) перекрываются, т.е. отличны от нуля в одних и тех же точках пространства. Поэтому при одинаковых характеристиках частицы совершенно неотличимы друг от друга.

Принцип тождественности приводит к важнейшему выводу: в силу абсолютной неразличимости одного и того же вида перестановка местами любых двух частиц в системе не приводит к изменению физического состояния системы.

Посмотрим, какие ограничения накладывает принцип тождественности на операторы физических величин функции состояния системы. Для этого учтем, что перестановка частиц в системе отображается в операторах и функциях состояния перестановкой соответствующих координат. Так, перестановка j -ой и k -ой частиц означает перестановку x_j и x_k.

Операторы физических величин должны быть симметричными относительно индексов частиц одного сорта, т.е. они не должны зависеть от нумерации этих частиц в системе. Этому правилу удовлетворяют все операторы, введенные ранее для системы.

Волновая функция системы при перестановке аргументов, относящихся к двум разным частицам, может изменяться только на физически несущественный фазовый множитель е^iα. Поэтому для функции состояния системы должно выполняться равенство:

.

Сделаем вторую перестановку координат двух рассматриваемых частиц в правой части этого равенства:

,

отсюда

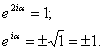
Следовательно, при перестановке координат любых двух частиц волновая функция либо только меняет знак, либо не изменяется. Функции первого типа называются антисимметричными, а второго  - симметричными (по отношению к перестановке частиц местами).

Симметрия функций состояния не зависит от взаимодействия и движения частиц в системе.