Механика системы микрочастиц, страница 2

.

Для нахождения функций ψ(х₁,х₂,…,х_N) нужно решить уравнение Шредингера без времени

 или

.                                             (9.1)

Одночастичные операторы Гамильтона действуют только на координаты i-той частицы. Поэтому переменные в уравнении (9.1) разделяются. Выполним подстановку:

.       (9.2)

Получаем

,

разделим на ψ₁ψ₂…ψ_N

.

Подставим энергию системы Е в виде слагаемых, имеющих смысл энергии отдельных частиц. Значения последних находятся из уравнений:

,                                                           (9.3)

на которые распадается уравнение (9.1).

Решив уравнение (9.3), мы найдем уровни энергии и волновые функции для каждой частицы. Каждый уровень и каждая функция определяется некоторым набором квантовых чисел, обозначающихся через n_i (например, для электрона в кулоновском поле набор представляет совокупность четырех чисел: n, , m, m_s). Индекс i дает номер частицы, к которой относится набор.

Итак, для системы:

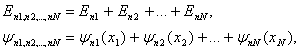
- функция состояния системы невзаимодействующих частиц находится как произведение одночастичных функций.

Можно показать, что четность состояния системы частиц равна произведению четностей состояния отдельных частиц:

.

Если частицы в системе одинаковы, например, это электроны, то все уравнения (9.3) имеют один и тот же вид. Это означает, что спектр функций состояния и уровней энергии один и тот же для всех частиц. Квантовые состояния системы можно получить, составляя различные комбинации по N – одночастичных состояний. Все эти состояния определяются выборками по N из бесконечного числа наборов квантовых чисел n, определяющих состояние одного электрона в некотором поле.

9.2. Тождественность частиц одного и того же вида и

принцип Паули

В системе микрочастиц проявляются также физические закономерности, которые не могут быть установлены при анализе движения одной микрочастицы.

Квантовая система, состоящая из одинаковых частиц, например, электронов, протонов, фотонов и т.д., обладает некоторыми новыми свойствами, не имеющими аналога в классической физике. Они связаны с абсолютной тождественностью частиц одного и того же вида. В макромире всегда можно различить два тела по массе, заряду, энергии и т.д. Все эти величины в классической физике считаются изменяющимися непрерывно, так что вопрос о различии параметров частиц сводится к степени точности измерений. Более того, при совпадении всех характеристик частиц одного и того же вида всегда можно отличить частицы друг от друга, постоянно следя за движением каждой частицы по своей траектории.

В микромире имеют место дискретные значения величин, характеризующих микрочастицы. Внутренние параметры у частиц одного вида совершенно одинаковы, так, у всех электронов одинаковы масса, заряд, спин. Если частицы находятся в одинаковых состояниях, то совпадают и параметры состояний: у них одинаковые энергия в связанном состоянии, момент импульса и его проекция, проекция спина. Абсолютное совпадение характеристик микрочастиц одного вида приводит к их тождественности, принципиальной неразличимости. Это положение носит название принципа тождественности частиц и является постулатом квантовой механики системы частиц.