2.3. Привод постоянной частоты вращения как объект регулирования частоты
Для исследования статики и динамики процессов регулирования частоты генераторов необходимо иметь дифференциальные уравнения элементов системы регулирования. Характер процессов зависит от свойств объекта регулирования — привода постоянной частоты вращения. В общем случае процесс регулирования частоты связан с процессом регулирования напряжения синхронного генератора, т. е. система генератор — привод является двухмерной системой регулирования. Для агрегата, состоящего из привода и синхронного генератора, уравнение равновесия моментов на валу имеет вид
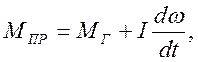 (2.16)
(2.16)
где МПР — момент, развиваемый ППЧВ; МГ — момент нагрузки, создаваемый генератором; I — момент инерции всех орошающихся частей, приведенный к валу генератора; ω — угловая скорость выходного вала ППЧВ.
Момент, создаваемый приводом, зависит от угловой скорости авиационного двигателя ωад, угловой скорости выходного вала ППЧВ ω и от углового положения регулирующего органа γ (угла наклона управляемой шайбы гидронасоса гидравлического ППЧВ или угла поворота дроссельной заслонки пневматического привода):
![]() (2.17)
(2.17)
Момент нагрузки синхронного генератора зависит от его активной мощности Ри и угловой скорости вращения ω:
МГ = Ра/ω (2.18)
Если полагать, что нагрузка генератора носит активно-индуктивный характер, причем индуктивность и активное сопротивление подключены параллельно, то уравнение (2.I8) можно записать в виде
МГ = U2 / (Rω). (2.19)
где U — напряжение па зажимах генератора
Уравнения (2.16). (2.17), (2.19) являются нелинейными, что затрудняет их анализ. Но если рассматривать процесс в квазиустановившемся режиме, т.е. когда отклонения всех переменных незначительны от их установившегося значения, то уравнения (2.16). (2.17), (2.19) можно заменить приближенными линейными.
Тогда уравнение (2.16) примет вид
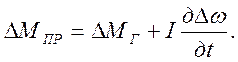 (2.20)
(2.20)
Уравнение (2.17)
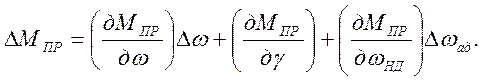 (2.21)
(2.21)
а уравнение (2.19)
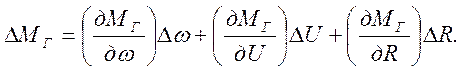 (2.22)
(2.22)
где 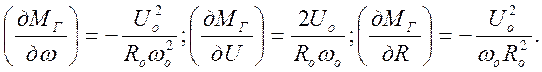
Индекс «о» соответствует значению параметра в установившемся режиме.
Подставляя (2.22) и (2.21) в (2.20), получим
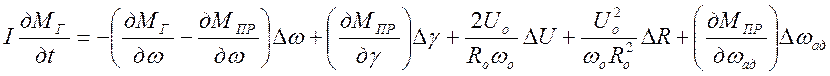 . (2.23)
. (2.23)
Уравнение (2.23) можно представить в безразмерной форме, разделив правые и левые его части на установившееся значение момента.
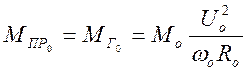 .
.
После соответствующих преобразований
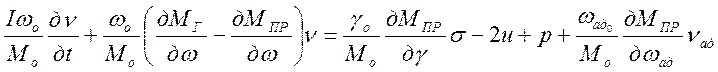 (2.24)
(2.24)
где ν =Δω/ωо — относительное изменение угловой скорости выходного вала ППЧВ; σ = Δγ/γо — относительное изменение положения регулирующего органа; u = ΔU/Uo— относительное изменение напряжения генератора; ρ = ΔR/Rо —относительное изменение активного сопротивления нагрузки; νад = Δωад/ωад0 — относительное изменение возмущающего воздействия угловой скорости авиационного двигателя.
В операторной форме при нулевых начальных условиях уравнение (2.24) записывается в виде
![]() (2.25)
(2.25)
где ТМ = Iωo/Mo – постоянная
времени привода; 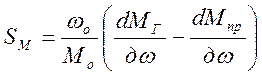 – коэффициент
самовыравнивания привода;
– коэффициент
самовыравнивания привода; 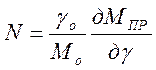 – коэффициент усиления
привода по параметру управления;
– коэффициент усиления
привода по параметру управления; 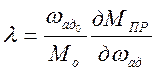 – коэффициент, характеризующий влияние возмущающего воздействия.
– коэффициент, характеризующий влияние возмущающего воздействия.
Коэффициент самовыравнивания SМ характеризует статическую устойчивость привода. При SM > 0 привод постоянной скорости статически устойчив.
Рассмотрим несколько вариантов взаимного расположения механических характеристик генератора и привода (рис. 2.9). Точка m на этих графиках характеризует равновесное состояние, когда Мпр (ω) = МГ (ω) = М0.
На рис. 2.9.а показан случай, когда SМ>0. При случайном увеличении угловой скорости на величину Δω момент привода Мпр становится меньше момента нагрузки МГ создаваемого генератором (Мг > /МПР), и привод притормаживается до тех пор, пока угловая скорость не достигнет значения ωо.
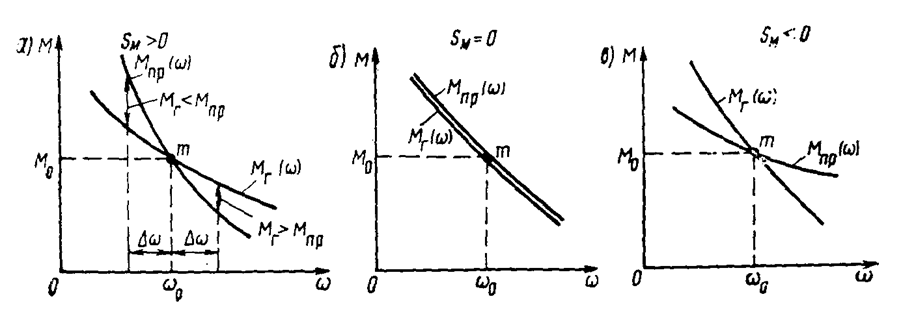
Рис. 2.9. Зависимость момента привода и генератора от угловой скорости: а – SM>0; б – SM=0; в – SM<0.
При уменьшении угловой скорости на Δω Мг<Мпр, и привод будет разгоняться до тех пор, пока не наступит первоначальное состояние равновесия ωо, Мо.
На рис. 2.9, б изображено соотношение характеристик, соответствующее SМ = 0. Как следует из уравнения (2.25), в этом случае привод представляет собой интегрирующее звено, у которого нет положения устойчивого равновесия. Для расположения кривых моментов привода и генератора (рис. 2.9, в, SM < 0) любое отклонение угловой скорости от своего значения при равновесном состоянии ωо, Мо приводит к нарушению устойчивости системы; при случайном небольшом увеличении угловой скорости Мпр< Мг, и скорость продолжает расти; при ее уменьшении Мпр < Мг угловая скорость продолжает уменьшаться и привод останавливается, т. е. система находится в неустойчивом состоянии.
Из приведенного анализа следует, что с точки зрения устойчивости системы регулирования частоты предпочтительно иметь ППЧВ с жесткими механическими характеристиками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.