Сопротивление материалов: Практикум, страница 2

1.  Что мы называем стержнем?

2.  В чем суть метода сечений?

3.  Внутренние силы при осевом растяжении – сжатии.

4.  Определение  и размерность нормальных и касательных  напряжений.

5.  Закон Гука при растяжении – сжатии.

6.  Правила построения эпюр  внутренних сил, напряжений и перемещений.

7.  Как определяются опасные сечения?

8.  Три вида задач из условия прочности.

Задача: Для заданной схемы нагружения стержня, изображенной на

рис. 1а), осевыми нагрузками проверить опасные сечения (участок) на прочность, если задано: величина нагрузки  F = 12,0 кН,  площадь поперечного сечения  участка стержня А = 150 мм²; допускаемое напряжение [s] = 170 МПа, модуль упругости при растяжении-сжатии Е = 2×10⁵  МПа, длина участка стержня а = 0,5 м.

          Методические указания к решению задания:

-  разбиваем стержень на участки;

-  применяем метод сечений для определения нормальных сил;

-  определяем напряжения на каждом из участков стержня;

-  находим опасное сечение стержня и проверяем его на прочность;

-  определяем перемещения на каждом участке стержня;

-  строим эпюры нормальных сил, напряжений и перемещений стержня.

Данный алгоритм реализуем при решении задачи:  

1. В начале решения стержень разбиваем на участки. Это разделение проводится с учетом изменения нагрузки или площади поперечного сечения стержня при переходе от одного участка к другому.

          Для данной  на рис. 1а) схемы нагружения стержня разбиваем его на три участка: первый - ВС; второй - СD и третий - DE.

          2. Определяем нормальные силы (внутренние силовые факторы) на каждом из участков методом сечений. Для этого мысленно рассекаем стержень

 

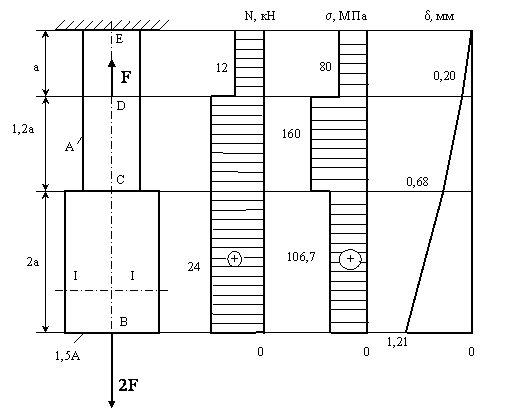                                 а)                      б)                      в)               г)

Рис. 1

           плоскостью, перпендикулярной оси стержня, например I-I, на первом участке, отбрасываем одну из  его частей и рассматриваем равновесие оставшейся части, проецируя все силы на вертикальную ось стержня. В нашем примере это нижняя часть стержня от точки В до плоскости I-I.

Знак нормальной силы в сечении определяется так: если нагрузка на данном участке направлена от сечения, то нормальная сила положительна, т.е. на этом участке стержень растягивается; в противном случае нормальная сила отрицательна, а стержень – сжимается. В нашем примере, на первом участке ВС нагрузка величиной 2F направлена от сечения I-I (рис.1а)), значит уравнение равновесия имеет вид:

N₁ – 2F = 0,

отсюда  нормальная сила

N₁ =  2F = 2×12 = 24 кН,

т.е. на этом участке стержня имеет место его растяжение.

Применяя метод сечений на других участках стержня, получим:

-  второй участок СD: N₂ = 2F  = 2×12 = 24 кН – растяжение;

-  третий участок DE: N₃ = 2F – F = F = 12 кН – растяжение.

3. Напряжение на каждом участке определяем как отношение нормальной силы к площади поперечного сечения стержня:

s₁= N₁ / (1,5 А) = 2F / (1,5A) = 2×12×10³/(1,5×150) = 106,7 МПа;

s₂ = N₂ / А = 2F / A = 2×12×10³/150 = 160,0 МПа;

   s₃ = N₃ / А = F / A = 12×10³/150 = 80,0 МПа.

4. Определяем опасное сечение. Оно находится по наибольшей величине напряжения. В нашем примере это  второй участок - CD, где каждое сечение является опасным, т.к.