2.4. Анализ статики и динамики процессов регулирования частоты
Для оценки динамических и статических характеристик системы регулирования частоты (время переходного процесса, погрешность в установившемся режиме и др.) анализируется математическая модель системы. В процессе анализа выявляют влияние отдельных элементов системы регулирования на ее устойчивость, определяют области возможных значений ее параметров, а также их значения, обеспечивающие высокое качество переходных процессов.
Проведем анализ системы регулирования частоты, имеющей точный и грубый каналы регулирования, при одиночной работе синхронного генератора. Уравнение объекта регулирования, состоящего из синхронного генератора и ППЧВ, согласно (2.25) имеет вид
![]() (2.26)
(2.26)
Грубый и точный каналы регулирования описываются уравнениями (2.10) и (2.25):
![]() (2.27)
(2.27)
![]() (2.28)
(2.28)
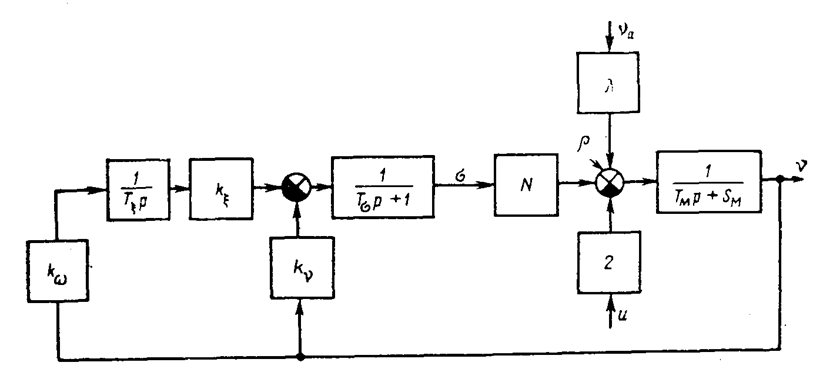
Рис 2.10. Структурной схемы системы регулирования частоты вращения синхронного генератора.
Уравнениям (2.26) – (2.28) соответствует структурная схема, привсденнаая на рис. 2.10.
Процесс регулирования частоты протекает значительно медленнее, чем процесс регулирования напряжения, поэтому систему регулирования частоты в ряде случаев можно рассматривать как одномерную, полагая, что u = 0, т. е. частота регулируется при постоянном напряжении генератора.
Исключив из системы уравнений (2.26) — (2.28) σ и ε, получим уравнение стабилизации угловой скорости
![]() (2.29)
(2.29)
Для оценки устойчивости системы воспользуемся критерием Гурвица. Характеристическое уравнение системы имеет вид
![]() (2.30)
(2.30)
Для системы третьего порядка необходимыми условиями устойчивости являются требования положительности всех коэффициентов характеристического уравнении и выполнения неравенства
![]() (2.31)
(2.31)
Первое условие устойчивости требует положительности коэффициентов уравнения (2.30). Так как Nkν > SМ, то это условие сводится к неравенству
TM > -SMTσ. (2.32)
Коэффициент самовыравнивапня для пневмопривода может быть отрицательным при максимальной угловой скорости авиадвигатели. Для выполнения условия (2.32) необходимо увеличивать Tσ или уменьшать Тм, однако увеличение постоянной привода приведет к затягиванию переходного процесса.
Неравенство (2.31) можно записать так:
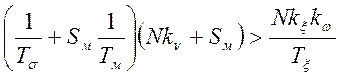 . (2.33)
. (2.33)
Из формулы следует, что повышение коэффициента усиления системы Nkξkω снижает запас устойчивости, а уменьшение постоянных привода Тм и регулятора Тσ увеличивает устойчивость. Из (2.33) также следует, что наличие точного канала регулирования частоты (Tσ ≠ ∞) приводит к ухудшению динамических свойств системы регулирования. Для расширения области устойчивости желательно увеличивать время перекладки шайбы исполнительного двигателя Тξ. но увеличение Тξ приводит к затягиванию переходного процесса.
Постоянные времени пневматических приводов лежат в пределах: Тм = 1.5–З с; Тσ = 0,3–0.8 с; Тξ = 0.1–0,3 с. Коэффициент самовыравнивания на номинальных режимах работы авиадвигателя SM = 0,8–1.5. Для гидромеханических приводов Тм = 0,5–0,8 с, а значения Тσ и Тξ примерно те же, что и для пневматических приводов. Благодаря тому, что постоянная времени гидромеханических приводов меньше, чем у пневмоприводов, они обеспечивают более высокое быстродействие системы регулирования частоты.
На рис. 2.11, а приведена осциллограмма переходного процесса по частоте для пневмопривода при подключении к генератору половины его номинальной активной нагрузки. На рис. 2.11, б показан процесс регулирования частоты интегрального гидромеханического ППЧВ при возникновении трехфазного короткого замыкания синхронного генератора и его отключении.
Для оценки влияния параметров системы на точность регулирования в установившемся режиме положим в уравнении (3.29) р = 0 (t = ∞). Из уравнения следует, что статическая ошибка регулирования частоты v = 0, так как в системе используется интегрирующее звено — конденсаторный двигатель.
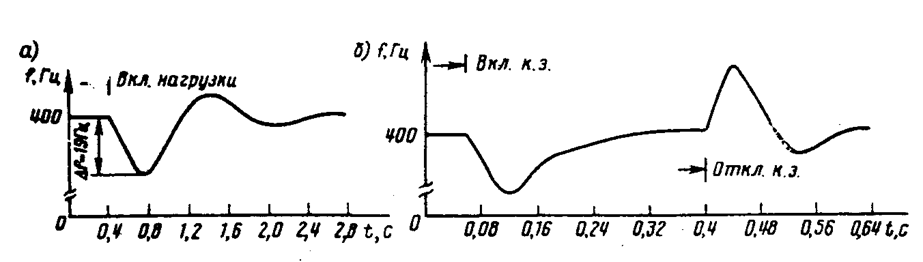
Рис. 2.11. Переходные процессы регулирования частоты.
Однако в действительности статическая ошибка отлична от нуля и составляет примерно 0,25%. Это объясняется тем, что при выводе уравнения точного канала регулирования не учитывался момент трогания конденсаторного двигателя. При отсутствии точного канала статическая ошибка
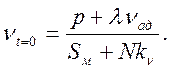 (2.34)
(2.34)
Статическая ошибка в реальных системах составляет 1—5 %.
При выводе уравнений (2.26)—(2.28) не учитывался ряд факторов, которые имеют место в реальных системах: наличие люфтов в звеньях пневмо-и гидромеханических передач; влияние сжимаемости жидкости под действием находящегося в ней воздуха: наличие трения между элементами ППЧВ; действие вибрации, температуры и т. д. Поэтому в реальных системах стабилизации частоты для повышения точности и устойчивости процессов регулировании могут устанавливаться дополнительные корректоры, обратные связи, демпферы.
Применяемые в системах регулирования частоты генераторов переменного тока регуляторы и их корректоры поставляются в отлаженном состоянии и в процессе эксплуатации не требуют дополнительной регулировки.
Вопросы для самоконтроля
1. В чем заключается принципиальная разница между регуляторами угловой скорости и регулятором частоты тока?
2. Чем определяется статизм регулятора угловой скорости?
3. Чем вызвана необходимость в применении корректоров частоты и от чего зависит погрешность корректоров частоты?
4. Изменится ли статическая ошибка регулирования угловой скорости, если устранить, связь поршней золотника с гидравлическим сервомотором?
5. Как влияют постоянные времени регулятора угловой скорости и корректора частоты на переходный процесс?
6. Что такое коэффициент самовыравнивания и от чего он зависит?
7. Какой элемент центробежно-гидравлического регулятора угловой скорости делает этот регулятор статическим?
8. Как влияет коэффициент редукции исполнительного двигателя корректора частоты па область устойчивости регулирования частоты?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.