Частица в одномерной потенциальной яме бесконечной глубины

Санкт-Петербургский  государственный горный  институт им. Г.В. Плеханова

(технический университет)

Расчетно-графическое задание

По дисциплине:                                                      Физика

                                       (наименование учебной дисциплины согласно учебному плану)

Тема:                           Частица в одномерной потенциальной яме бесконечной глубины.

Выполнил: студент     гр. АПМ-02       ______________                                            /Аверьянов Д.А./

                                                                                                             ^{(подпись)                                                                                              (Ф.И.О.)}  

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛ:

Преподаватель:     Доцент                          ____________                                          / Стоянова Т.В../

                                              ^{(должность)                                                (подпись)                                                                                     (Ф.И.О.)}

Санкт-Петербург

2004.

I.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Основополагающей в квантовой механике служит идея о том, что корпускулярно – волновая двойственность свойств, установленная для света, имеет универсальный характер. Все движущиеся частицы обладают волновыми свойствами.

Формула де Бройля устанавливает зависимость длины волны, связанной с движущейся частицей вещества, от импульса  частицы,

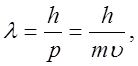
где m- масса частицы, - ее скорость, h- постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля.

Другой вид формулы де Бройля:

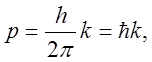
где 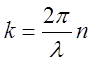- волновой вектор, модуль которого 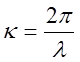- волновое число – есть число длин волн, укладывающихся на единицах длины, n-единичный вектор в направлении распространения волны,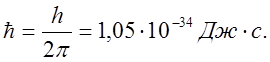

Положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции (пси-функции) Вероятность того, что частица находится в момент времени t в малом объеме  вблизи точки М(x ,y, z), равна:

где - квадрат модуля волновой функции. Величина есть плотность вероятности пребывания частицы в данной точке пространства: 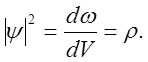Интенсивность волны де Бройля определяется величиной .

Потенциальной ямой называется область пространства, в которой потенциальная энергия U частицы монотонно возрастает по мере удаления от точки, где эта энергия минимальна. На рис.1. изображена одномерная потенциальная яма бесконечной глубины с «плоским дном»:

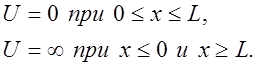
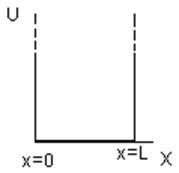
Рис.1. Одномерная потенциальная яма.

Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными (квантование физических величин). Собственные значения энергии Е_n в одномерной потенциальной яме бесконечной глубины:

 

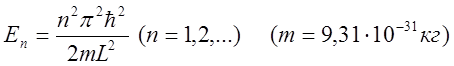
представляют собой дискретный ряд значений энергии, которая является квантованной.

Квантовые значения  Е_n   называются уровнями энергии, а число n, определяющее энергетические уровни частицы в потенциальной яме, называется квантовым числом.

Потенциальные ямы, в которых находятся частицы, могут иметь сложную форму. Если потенциальная энергия частицы имеет вид изображенный на рис.2., то для перехода частицы из области 1в область 2 или обратно частице с энергией Е, удовлетворяющей условию 0<E<U_max , нужно преодолеть потенциальный барьер. Из рис.2. видно, что высота барьера H=U_max-E и его ширина a зависят от значения Е.

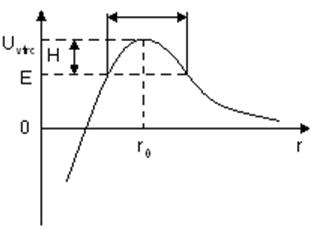
Рис.2.Потенциальная энергия частицы.

Согласно представлениям классической механики частица с энергией Е<U_max  не может преодолеть потенциальный барьер, т.е. перейти из области 1 в область 2 или обратно. Для такого перехода ей необходимо сообщить дополнительную энергию, равную или большую H.

В квантовой механике есть отличная от нуля вероятность D того, что частица, энергия которой Е<U_max  , может пройти «просочиться» сквозь потенциальный барьер. Вероятность D просачивания частицы называется прозрачностью (коэффициентом прозрачности) потенциального барьера для этой частицы.

Для прямоугольного потенциального барьера высотой U₀ и шириной L рис.3. прозрачность барьера выражается формулой:

.

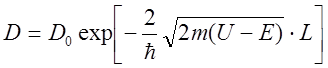Здесь m- масса, Е- энергия частицы.

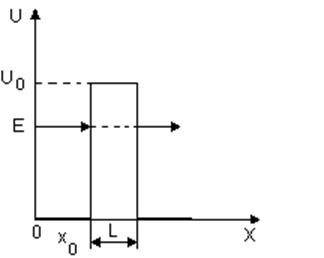
Рис.3. Прямоугольный потенциальный барьер.

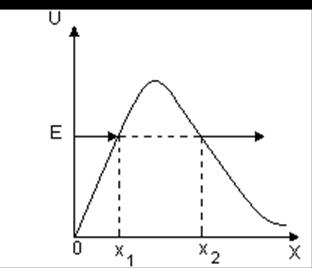
Рис.4.Потенциальный барьер сложной формы

Для потенциального барьера сложной формы:

,

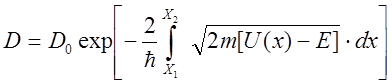где x₁ и x₂ –координаты начала и конца потенциального барьера U(x) для данного значения энергии Е (рис.4.). В этих формулах D₀ – постоянный коэффициент, близкий к единице.

Состояние частицы в пространстве задается волновой функцией. Это главное уравнение квантов физики φ(х). Основные свойства волновой функции:

- Функция конечна (вероятность не больше 1), однозначна и непрерывна.

- Производные от волновой функции по координатам и по времени должны быть непрерывны

- |φ(х)|² должна быть интегрируема, т.е. должна быть конечна.