Явление вращательного движения и понятия момента силы, пары сил, момента инерции, угловой скорости, углового ускорения

  

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный  институт им. Г.В. Плеханова

(технический университет)

Расчётно-графическое работа.

По дисциплине:

                                                         Физика              

                    (наименование учебной дисциплины согласно учебному плану)

Вариант-16

Выполнил: студент  гр. НБ-03     ______________    /Мухаметшин Г.Р./

                                                                                                     ^{(подпись)                                  (Ф.И.О.)}  

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛА:

                                 доцент              ____________            /Смирнова Н.Н./

                                                 ^{(должность)                        (подпись)                                         (Ф.И.О.)}

Санкт-Петербург

2004 год.

Задача.

    Обруч массой 455*10^-3 кг. вращается без начальной скорости вокруг своей оси. На обруч действуют пара сил с моментом М=24 Дж и моментом сопротивления М_сопр= (κ•ω²) Дж. Сколько оборотов сделает обруч до того, как его угловая скорость станет равной 3,11 рад/с?  (к=2,33 кг*м²;  R=0,46 м.)

Краткое теоретическое содержание:

В данной задаче рассматривается явление вращательного движения и понятия момента силы, пары сил, момента инерции, угловой скорости, углового ускорения.

   Вращательное движение твёрдого тела – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

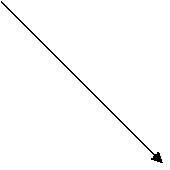
   Момент силы относительно неподвижной точки– это физическая величина, определяемая векторным произведением радиуса-вектора, проведённого из точки О в точку А приложения силы, на силу  (см. рисунок 1):

                                     

 

(Рис.1)

=[].

   Здесь  – псевдовектор, его направление совпадает с направлением поступательного движения правого  при его вращении от  

   Модуль момента силы

                                                    

де α – угол между  и ; rsinα=l – плечо силы.

 Плечо силы – длина  перпендикулярно-опущенная   из  заданной  точки  на  прямую,  вдоль  которой  действует  сила.

Момент силы относительно неподвижной оси  – проекция  момента  силы  относительно  точки  на  ось  произвольно  проходящей  через  данную  точку.

 М- скалярная величина,  не  зависящая  от  выбора  положения  точки  на  ось.

 - момента силы.

  Пара сил – это две равные по модулю,  но противоположные   по направлению и не действующие вдоль одной прямой силы. Плечо  пары-расстояние  между  прямыми,  вдоль  которых  действуют  силы.

Угловая скорость – это векторная величина ω,  модуль  которой  опредиляется  пределом  отношения  поворота  тела  на  угол ▲φ  за  время  ▲t  к  этому  времени,  при  стремлении  последнего  к  нулю:

                                                                  

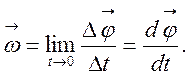
где    - изменение угла поворота за время .

  Модуль угловой скорости –величина, которая определяет угол поворота в единицу времени и характеризует быстроту вращения:

                                                 

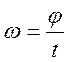
Единица угловой скорости []=1 рад/с.

   Угловое ускорение – это векторная величина, определяемая первой производной угловой скорости по времени:

                                          =.

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.

 Модуль углового ускорения – величина,характеризующая изме-нение модуля угловой скорости в течении времени.

Единицы измерения угловой скорости [] =рад/с

   Момент инерции тела относительно оси вращения -это физическая величина, равная сумме произведений  элементарных масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

J .

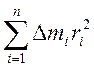В случае непрерывного распределения масс эта сумма сводится к интегралу:

                                                 J=,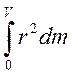

Величина r в данном случае есть функция положения точки с координатами x,y,z.

Дано:                                Решение:                                                                                                                                                                                                                                                                                                                                                                                

R= 0,46м                                                                                                                                      

m=455г=                                                                                                                                      

=0,455кг                                                                                                                                       

М=24 Дж                                                                                                                             =kω²                                                                                                                                 

k=2,33 кг•м                                                                                                                                 

ω=3,11 рад/с                                                                                                                                    

Найти:                                                                                                                                    n -? 

Уравнением динамики вращательного движения твёрдого тела  относительно  неподвижной  оси:

                                         _z,

где  - проекция углового ускорения на ось Z[]=рад/с²;

J- момент  инерции  тела  относительно  оси  Z [J]=кг*м²;

М_внеш.z- проекция  момента  силы  на  ось Z[М_внеш.z]=H*м.

(знак «-» показывает, что работа, совершаемая моментом сопротивления, идёт на торможение вращения обруча).

                        M – M=,

где M – момент силы вращения; [M]=Дж;

        - момент сопротивления; [M]=Дж.

       =kω²

Момент инерции обруча равен:

где m – масса обруча;       [m]=кг;

       r – радиус основания; [r]=м.

т.к.  

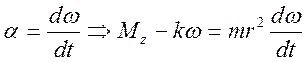
Преобразуем  угловое  ускорение:

=

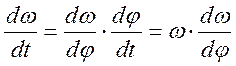
Запишем  подругому φ:

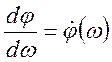    следовательно  φ=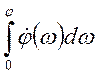

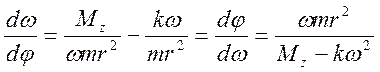
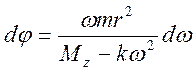  или:

  =

=

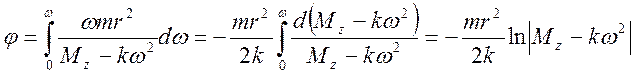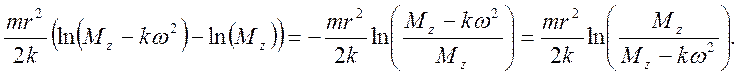
   Число оборотов, совершаемое обручом равно:

,

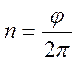где  - угол поворота; []=рад.

Колличество оборотов сделанных  обручем  равно:

n=.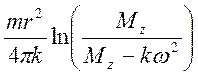

n=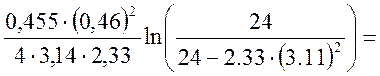

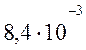
n=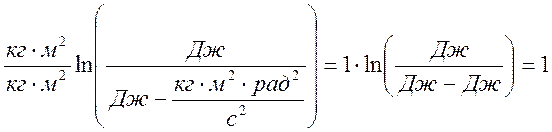

   Вывод:   В  данной  расчётно-графической  работе  было  получено  количество  оборотов  равной  8,4*10^-3, сделанным  обручем, до  того,  как  его  угловая  скорость  стала  равной   = 3,11 рад/с.