Аппроксимация кривой намагничивания методом гиперболического синуса и методом степенного ряда (методом наименьших квадратов)

Санкт-Петербургский государственный горный институт

имени  Г В. Плеханова (технический университет)

Кафедра общей электротехники.

Расчетно-графическое задание

Тема: «Аппроксимация кривой намагничивания.»

                                                                           Выполнил: студент Степаненко Д. Ю.

                                                                           Группа:  АПМ-01

                                                                           Проверил: доцент Анискин Б. Г. 

                                                                           Дата:____________________

Санкт-Петербург

2003

Вариант №1

Исходные данные:

H_св=44кА/м  В_r=0.95Тл 

H_А=37кА/м  В_А=0,77Тл

 H_Ц=5кА/м  В_Ц=0,16Тл

Задача 1

Аппроксимация кривой намагничивания методом гиперболического синуса.

Рис.1 Кривая размагничивания Н’=f(B)

На этой  кривой находим H’,а затем по формуле Н=Н_СВ-H’находим Н.

B	0,2	0,4	0,6	0,8
H	3	5	9	28

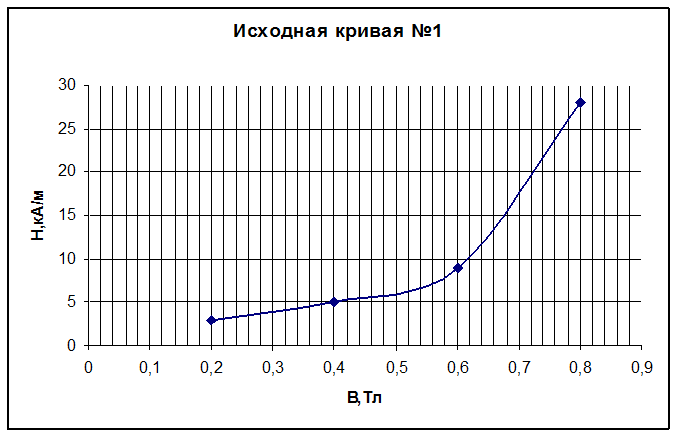
Рис.2. Исходная кривая №1

Аппроксимация кривой методом гиперболического синуса осуществляется с использованием формулы:

, где -коэффициенты.

На кривой №1 произвольно берем две точки с координатами Н₁=15;В₁=0,68 и

Н₂=20;В₂=0,72.

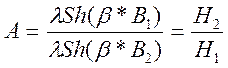
А=20/15=1,3

Для определения коэффициента  необходимо задать произвольные значения ,больше и меньше А.Получим таблицу:

	0,6	0,8	1,1	1,4	1,5
А	1,073	1,07	1,06	1,08	1,083

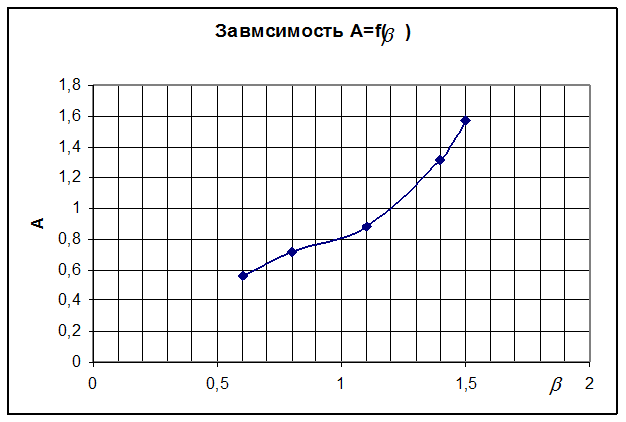
Рис.3. Зависимость А=f()

По графику находим что при А=1,3 =1,4

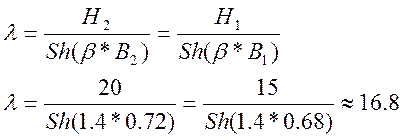
Н=16,8 Sh(1.4*B)-это кривая №2

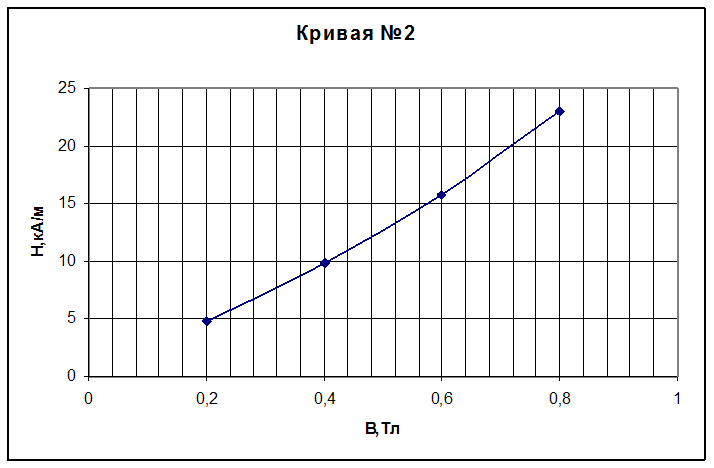
Рис.4. Кривая №2

Определяем ошибки аппроксимации кривой №1

-значение напряженности магнитного поля кривой №1

-значение напряженности магнитного поля кривой №2

B	0,2	0,4	0,6	0,8
	1,8	4,9	6,8	5

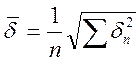
n=4-число заданных значений В

-сумма квадратов ошибок n уравнений

Задача №2

Аппроксимация кривой намагничиванияметодом степенного ряда(методом наименьших квадратов)

Н_К=а₁*В_К+ а₃*В²_К

Где а₁ и а₃ коэффициенты,которые можно найти из системы уравнений:

 

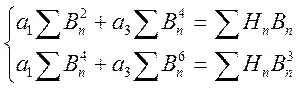
Расчитываем для В равных 0,2; 0,4; 0,6; 0,8.

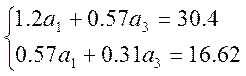
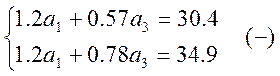
0,21=4,5

=21,4

Н=15,2В+21,4В³ -  кривая №3

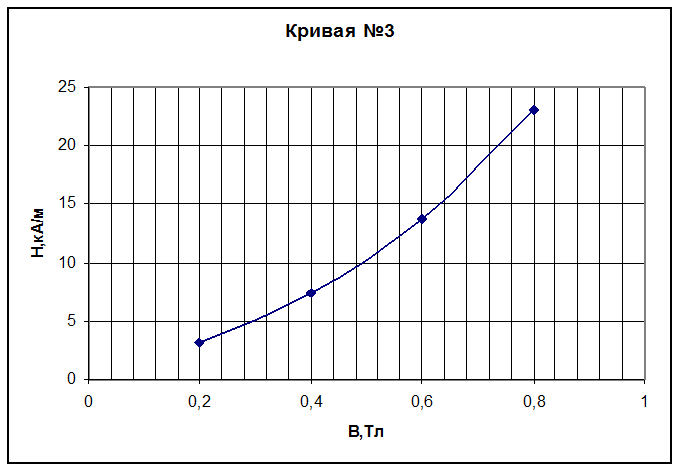
Рис.5. Кривая №3

Находим погрешность по формуле:

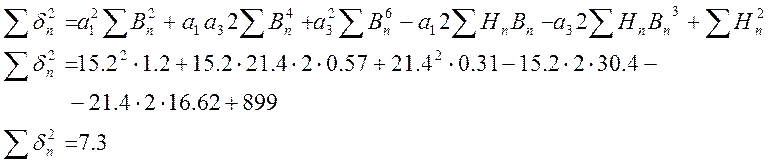
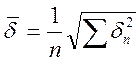
Вывод:

Выполнив аппроксимацию кривой намагничивания методом гиперболического синуса и методом наименьших квадратов, а затем, сравнив погрешности обоих методов () можно придти к заключению, что метод степенного ряда более подходит для аппроксимации кривой.

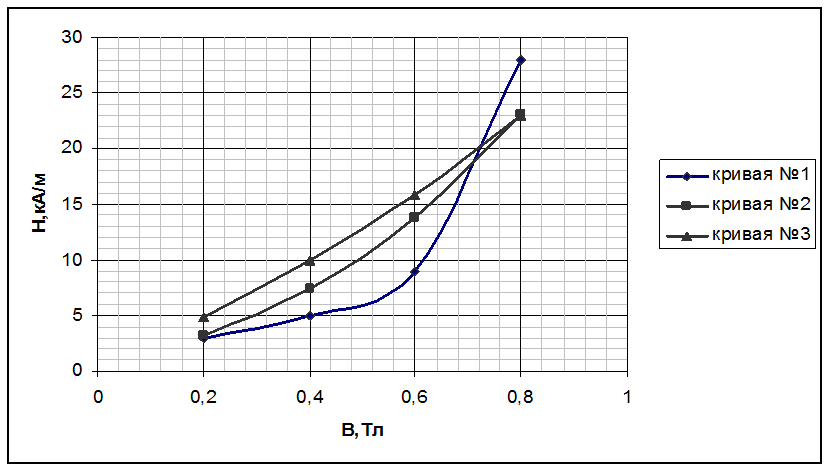
Рис.6. Сравнение методов аппроксимации.