§ 5. Формулы численного
интегрирования Гаусса
Наши формулы численного интегрирования будут иметь вид
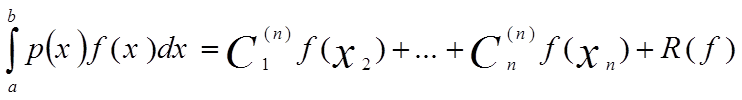
![]()
Здесь p(x)>0-фиксированная весовая функция, ![]()
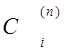 - постоянные коэффициенты, не зависящие от функции f(x), R(f)-остаточный член.
- постоянные коэффициенты, не зависящие от функции f(x), R(f)-остаточный член.
Если R(f)
обращается в нуль, когда![]()
![]()
![]()
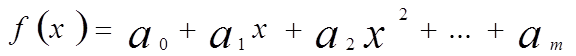
![]() ,
,
где коэффициенты ![]() произвольны, тo
произвольны, тo
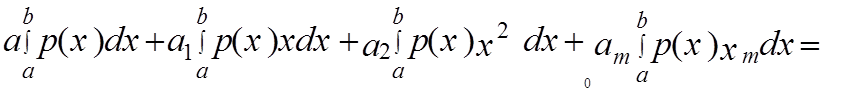
![]()
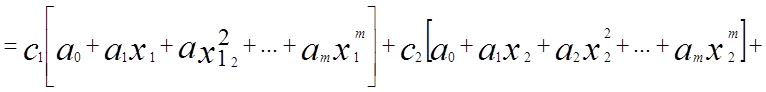
![]()
![]()
![]()
![]()
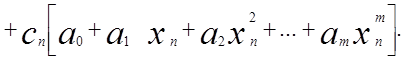
Обозначим
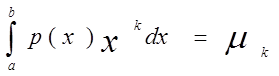 .
.
Будем отыскивать многочлен
![]()
где![]() -искомые
абсциссы. Оказывается,
-искомые
абсциссы. Оказывается, ![]() удовлетворяет довольно
несложному необходимому и достаточному условию, которое позволяет во многих
случаях его явно определить. Покажем, что
удовлетворяет довольно
несложному необходимому и достаточному условию, которое позволяет во многих
случаях его явно определить. Покажем, что
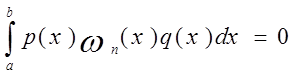 ,
,
если q(x)- произвольный многочлен степени не выше n-1.Действительно,
![]()
является многочленом степени
не выше 2n-1.Следовательно,
R(f)=0. ![]()
Таким образом,
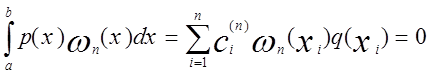 ,
,
так как
Обратно, если мы
найдем такой многочлен ![]() степени n
что
степени n
что
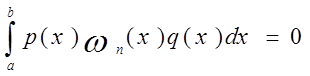 ,
,
когда q(x)-произвольный многочлен степени не выше n , и корни этого многочлена примем за узлы интерполирования, то в полученной при этом формуле численного интегрирования R(f) будет обращаться в нуль, когда f
является произвольным многочленом степени не выше 2n-1. .
Действительно, пусть f(x) является таким многочленом. Тогда
![]()
где q(x) и r(x)- многочлены степени не выше n-1 . Отсюда
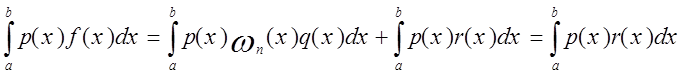
в силу нашего предположения. Но
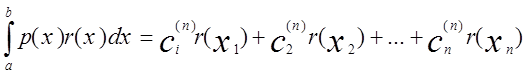 ,
,
так как r(x) как многочлен степени не выше n-1 совпадает со своим интерполяционным многочленом,
построенным по узлам ![]() ,.
,.
Кроме того,
![]()
таким образом,
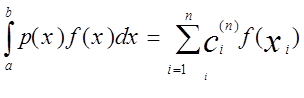
и R(f)=0 , что и требовалось доказать.
Коэффициенты формул Гаусса
Найдем теперь выражения для коэффициентов при ![]() , полученных формул численного
интегрирования. Для этого рассмотрим функцию
, полученных формул численного
интегрирования. Для этого рассмотрим функцию
![]()
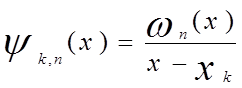
Квадрат этой функции является многочленом степени 2n-2. Следовательно,
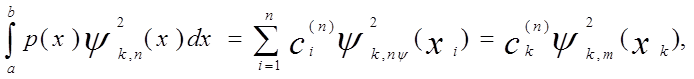
Отсюда
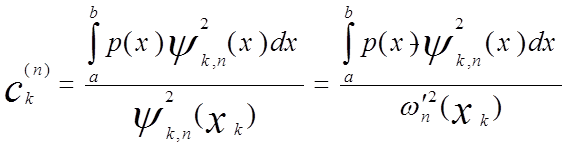 .
.
отметим здесь же, что все ![]() положительны.
положительны.
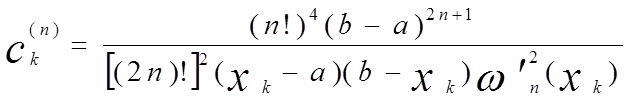 .
..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.