Задание 6. Вычислить интеграл по формуле Симпсона с
точностью ![]() =0,001.
=0,001.
1. 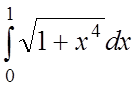 2.
2.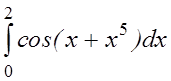
3.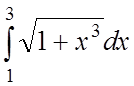 4.
4.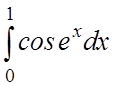
5.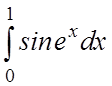 6.
6.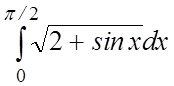
7.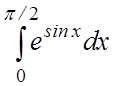 8.
8.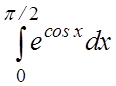
9.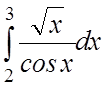 10.
10.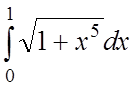
11.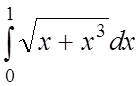 12.
12.
13.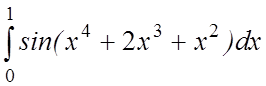 14.
14.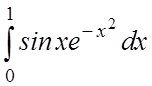
15.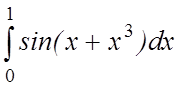 16.
16.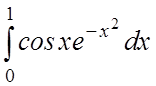
17.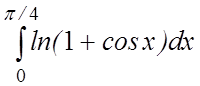 18.
18.
19.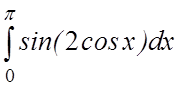 20.
20.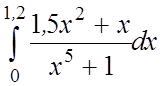
21.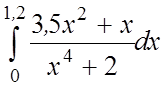 22.
22.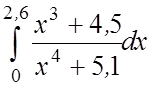
23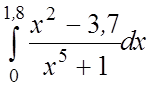 24.
24.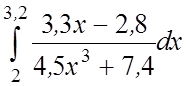
25.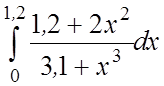 26.
26.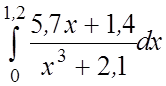
27.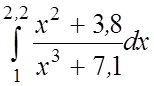 28.
28.
29.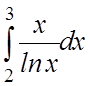 30.
30.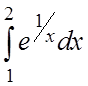
Задание 7. Численно решить задачу Коши для
дифференциального уравнения первого порядка с точностью ![]() =0,00001 , используя метод Рунге- Кутта
4-го порядка.
=0,00001 , используя метод Рунге- Кутта
4-го порядка.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
![]()
24. ![]()
25. ![]()
26. ![]()
27. ![]()
28. ![]()
29. ![]()
30. ![]()
Задание 8. Используя метод прогноза и коррекции, составить
решение краевой задачи для обыкновенного дифференциального уравнения с
точностью ![]()
1. 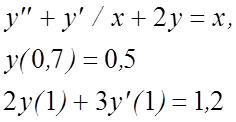 2.
2.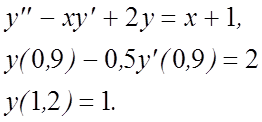
3.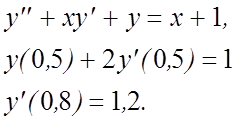 4.
4.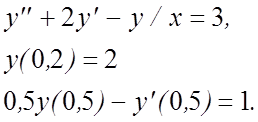
5.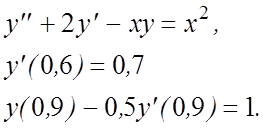
6 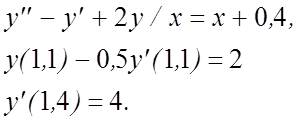
7.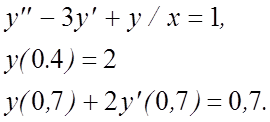
8.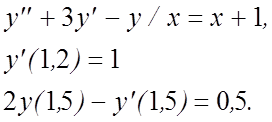
9.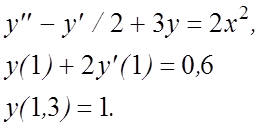
10.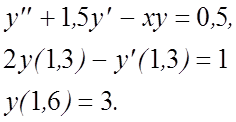
11.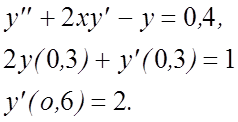
12.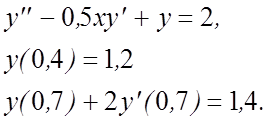
13.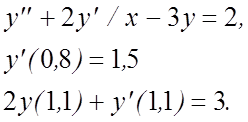
14.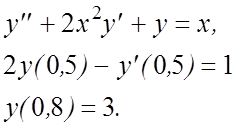
15.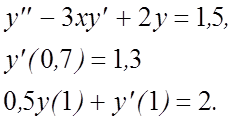
![]()
16.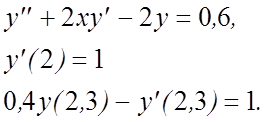
17.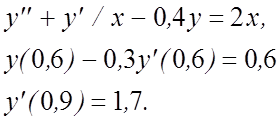
18.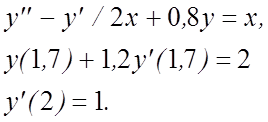
19.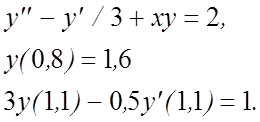
20.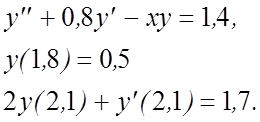
21.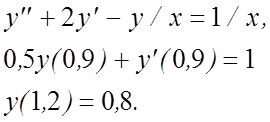
22.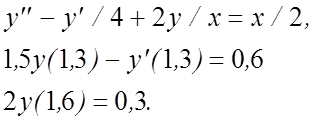
23.
24.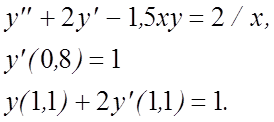
25.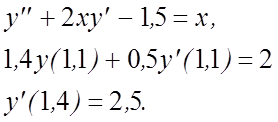
26.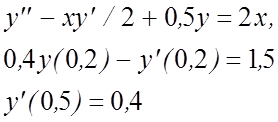
27.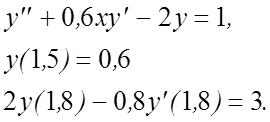
28.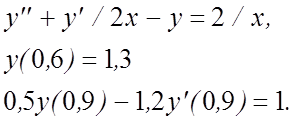
29.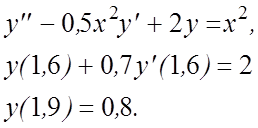
30.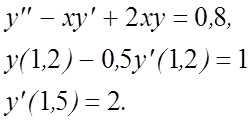
Задание 9. Методом градиентного спуска найти минимум функции при заданных начальных условиях
![]()
1.
![]() 0
0
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. ![]()
27. ![]()
28. 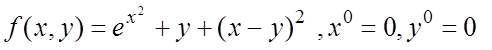
Задание 10 Найти экстремаль функционала в пространстве функций С с закрепленными концами
1. I(y)=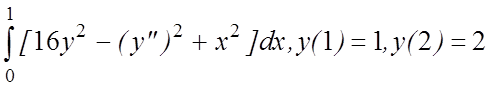
2. I(y)=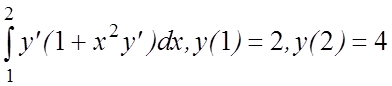
3. I(y)=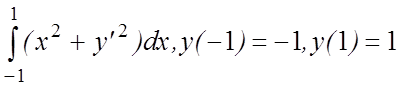
4. I(y)=2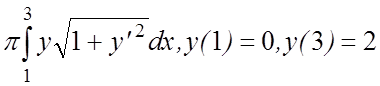
5. I(y)=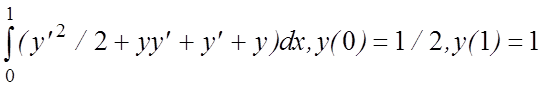
6. I(y)=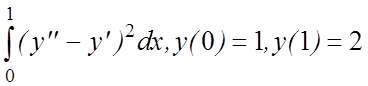
![]()
7. I(y)=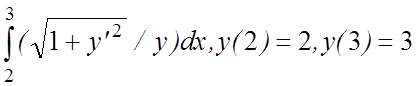
8. I(y)= 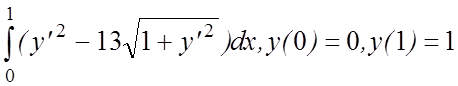
9. I(y)=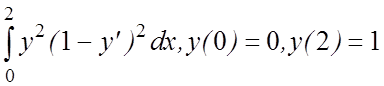
10. I(y)=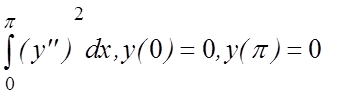
11. I(y)=
12. I(y)=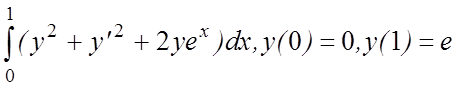
13. I(y)=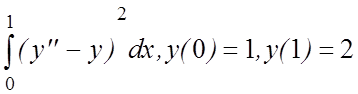
14. I(y)=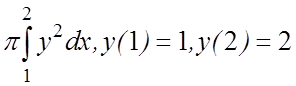
15. I(y)=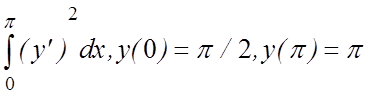
16. I(y)=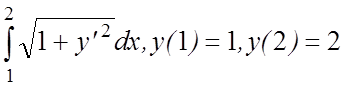
17. I(y)=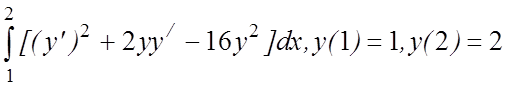
18. I(y)=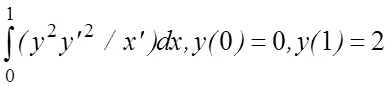
19. I(y)=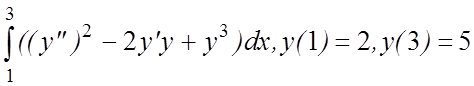
20. I(y)=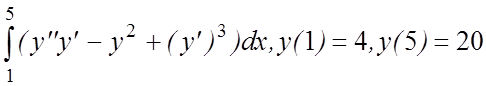
![]()
21. I(y)=
22. I(y)=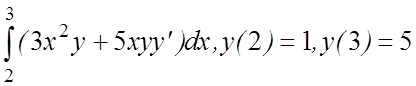
23. I(y)= 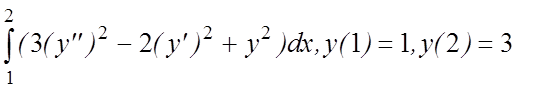
24. I(y)=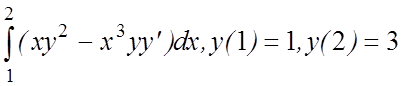
25. I(y)=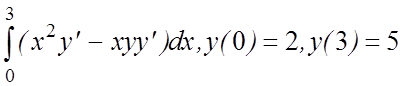
26. I(y)=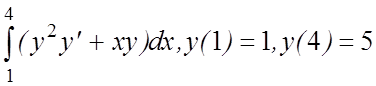
27. I(y)=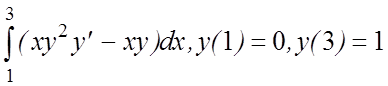
28. I(y)=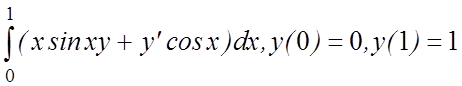
29. I(y)=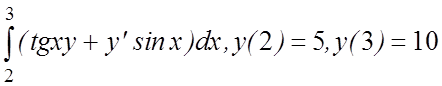
30. I(y)=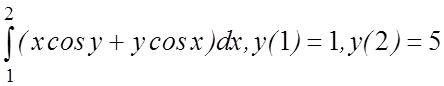
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.