Министерство Образования Украины
Сумский Государственный Университет
Кафедра Прикладной математики
по дисциплине Программирование и Численные методы
Анотация: в данной курсовой работе осуществляется расчет теплофизических свойств газов и газовых смесей компрессорного оборудования.
Студент Долгов Е.А.
Преподаватель Любчак В.А.
2001
ОБЩАЯ ХАРАКТЕРИСТИКА.
Этот программа предназначена для расчета теплофизических свойств рабочих тел компрессорного оборудования, т.е. газа и газовых смесей.
Расчет теплодинамических свойств газов и газовых смесей при температурах Т >1.3*Тс(критическое) базируется трехпараметрическом уравнении Ван-Дер-Вальса (ВДВ или VDW), при температурах Т<=1.3*Тс используется уравнение Редриха-Квонга(RK).
Программа обеспечивает расчет по заданному давлению Р и температуре Т следующие теплофизические характеристики газового состояния:
1. Параметрические параметры:
a. Плотность
b. Коэффициент сжимаемости
c. Производные от давления
d. Показатель адиабаты
e. Скорость звука
2. калорические свойства:
a. внутренняя энергия
b. энтальпия
c. энтропия
3. Коэффициент переноса:
a. Вязкость динамическая
b. Вязкость кинематическая
c. Теплопроводность
Номенклатура веществ приведена в файле tabl1.txt и может быть дополнена.
Все строки этого файла которые начинаются с символов ; # ' считаются комментариями, все остальные данные должны быть отделены друг от друга хотя бы 1 пробелом или знаком табуляции. Кроме этого необходим файл u.txt в котором хранится текстовая часть результатов выполнения программы.
Область применяемости данной методики ограничена интервалом температур от 240К до 600К (от -400С до 3500С). По довлениям предусмотрены следующие ограничения:
А) Уравнение РК позволяет рассчитать свойства газов при Т<0.9Тс вплоть до кривой насыщения. Предельные значения в этом случае определяются уравнением:
Pmax=Pc*Exp(as*(1-Tc/T))
Где аs=ln(9.8692*Pc)/(Tc/Tb-1)
Pc Критическое давление МПа
Tb нормальная температура кипения
При 0,9<=T/Tc<=1,3 предельное давление Pm=0,95Pc
Б) Уравнение ВДВ обеспечивает при Т>1,3Тс расчет до плотностей порядка 1,5rс, чему соответствует предельное давление
Pm=16.23*Pc(t+a(t-0.5))
Где t - приведенная температура;
a - коэффициент расчета Pm.
Объем исходной информации сведен к минимуму. Ввод ее предусмотрен в 2 этапа. На первом этапе вводится число компонентов газовой смеси, их названия и концентрации. На втором – температура Т и давление Р для условий, при которых определяются теплофизические свойства.
Разделение ввода исходной информации связано с возможностью повторных вычислений теплофизических свойств смеси одного и того же состава при различных Т и Р.
АЛГОРИТМ РАСЧЕТА.
1. Выбор компонентов из банка данных и ввод процентного соотношения смеси.
2. Определение псевдокритических параметров.
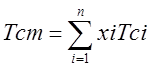
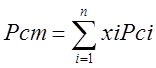
3. Определяется средняя молекулярная масса смеси и ее газовая постоянная
Rg*R/Mm
4. Осуществляется ввод Р и Т. После чего производится проверка условия 230<=T<=600. Если условие не выполняется, то выводится соответствующее сообщение и повторяется ввод данных. Если условие выполняется, то осуществляется проверка Т<=1.3Тс. При выполнении этого условия расчет продолжается по уравнению Редриха-Квонга, при невыполнении по уравнению Ван-дер-Вальса.
5. Формирование коэффициентов уравнение РК.
А=0,42748*(Р/Рс)/(Т/Тс)2,5
В=0,08664(Р/Рс)/(Т/Тс)
Для многокомпонентных смесей:
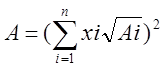
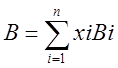
6. Формирование коэффициентов уравнения ВДВ.
к=ln(9.8692Pc)/(Tc/Tb-1)-3.5
Тb=Тс/(0,1839+0,123*к-0,0128*к2)
Ro=3905Pc/Tb
Для многокомпонентных смесей:
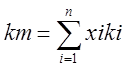
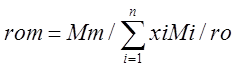
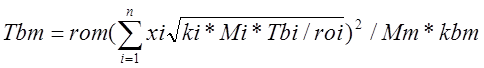
Pom=Rg*Tbm*rom/1000
7. Проверка применяемости методики по давлениям:
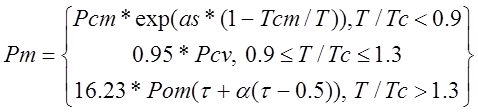
где t=T/Tbm; a=0.97*kbm/t0.125
Если Р<Рм, то расчет продолжается, в противном случае предлагается повторить ввод исходных данных.
8. Решение кубического уравнения.
В случае уравнения РК и ВДВ решение уравнения сводится к решению кубического уравнения
f(x)=ax3+bx2+cx+d=0
Для его решения применяется метод касательных Ньютона:
a) принимается начальное приближение x0=0;
b) Вычисляем f(x) и ее производную f’(x)=3ax2+2bx+c=0
c) Вычисляем последующее приближение x=x0-f(x0)/f’(x0);
d) Проверяем условие /x0/x-1/<=0.001
Если условие выполняется, то осуществляется выход из подпрограммы, в противном случае производится присваивание x0=x b и переход на пункт b.
Для РК
a=1 b=1 c=A-B(B+1) d=-AB
Для ВДВ
a=a b=a(t-1)-t c=t+p d=-p?
p=P/Pom
Выходными параметрами являются:
Для РК коэфициент сжимаемости z
Для ВДВ приведенная плотность w=ro/rom
После решения кубического уравнения определяются:
Для РК плотность газа ro=P/Rg*T*z
Для ВДВ коэффициент сжимаемости z=p/wt
9. Определение избыточности термодинамических свойств по уравнению РК
Энтропия ds=Rg(ln(1-B/z)-A/2B*Ln(1+b/z)+ln(0.1013*z/P))
Энтальпия dh=Rg*T(z-1-3A/2B*ln(1+B/z))
Внутренняя энергия du=-Rg*T(1+3A/2B*ln(1+B/z))
Изохорная теплоемкость dcv=Rg(3A/4B*ln(1+b/z))-1
Изобарная теплоемкость dcp=dcv+Rg*(zt2/zv-1), zt=z/(z-b)+a/(2(z+B)), zv=(z/(z-B))2-A((2z+B)/(z+B)2)
10. Определение избыточности термодинамических свойств по уравнению ВДВ.
Энтропия ds=Rg*a(7t*ln(1-w)-w)/8t
Энтальпия dh=Rg*Tb*a*(t*ln(1-w)-8tw/(1-w)+17w)/8
Внутренняя энергия du=-Rg*Tb*a*(t*ln(1-w)+9w)/8
Изохорная теплоемкость dcv=Rg*a*(9w-7t*ln(1-w))/64t
Изобарная теплоемкость dcp=dcv+Rg*(zt2/zv-1), zt=1+aw(7t/(1-w)+1)/8t
Zv=1+aw(t(2-w)/(1-w)2-2)/t
11. Определение идеально-газовых составляющих.
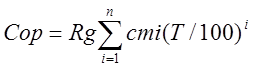
Cov=Cop-R;
S0=Rg((Cm1-1)*ln(T/100)+cm2(T/100)+cm3(T/100)2/2)
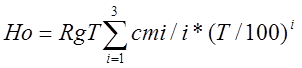
U0= H0-RgT
12. Определение термодинамических свойств при заданных условиях.
Pt’=Pzt/z*T
Pv’=-P2Zv/RgTZ2
Cv=Cov+dcv;
Cp=cop+dcp;
S=so+ds;
H=ho+dh;
U=uo+du;
Показатель адибаты kv=-Cp/Cv*Zv
Скорость звука ![]()
13. Определение коэффициентов переноса
Коэф. Вязкости
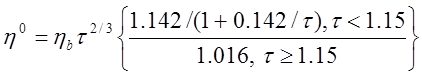
где ![]()
Коэф. Теплопроводности
![]()
где 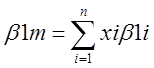
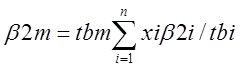
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.