Оценка функциональной эффективности классификации состояний, страница 2

                       D₂ = p( xÎ d / z Îd );                                                            (2.2.8)

где  x и z - соответственно измеренное и истинное значения параметра;

 d - поле допуска на значения параметра.

 

а) ошибка первого рода

 б) ошибка второго рода

 

в) первая достоверность

г) вторая достоверность

Рисунок 2.2.1 – Возможные исходы при двухальтернативном решении.

Разобьем множество возможных истинных значений контролируемого параметра на две области m₁ и m₂. Область m₁ включает значение параметра, находящегося в допуске, а m₂- не в допуске. Тогда вместо (2.2.5) - (2.2.8) можно записать:

       a = p(g₂  /m₁); b = p(g₁  /m₂); D₁ = p(g₁  /m₁); D₂ = p(g₂  /m₂);                  (2.2.9)

Из (2.2.9) следует для полных групп событий следующая связь между точностными характеристиками:

a + D₁=1; b + D₂= 1;                                                       (2.2.10)

Кроме того, вероятность принятия ошибочного решения на основании теоремы о полной вероятности равна:

                           P_ОШ= p(m₁)a + p(m₂)b ,                                                   (2.2.11)

а вероятность принятия правильного решения -

                           P_ПР = p(m₁)D₁ + p(m₂) D₂ ,                                              (2.2.12)

Выразив апостериорные вероятности p(g_m /m_l)  через априорные по формуле Байеса: 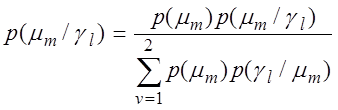                                                          (2.2.13)

и обозначив p(m₁) = p₁ и p(m₂) = p₂ с учетом (2.2.5) - (2.2.8) получим:

              

           

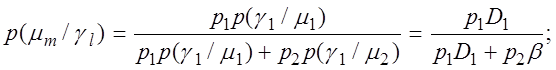
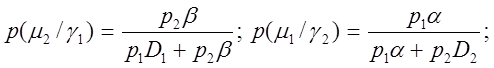
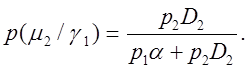                                                                                 (2.2.14)

После подстановки (2.2.14) в (2.2.4) при p₁= p₂=0.5  получим формулу для вычисления количества средней условной информации по точностным характеристикам СППР при двухальтернативном решении:

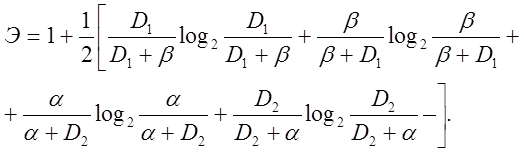                                         (2.2.15)

В общем случае, характеризующем процесс принятия решений, построенный на основании (2.2.15) график функции Э представляет поверхность в трехмерном пространстве.

На рисунке 2.2.2  показано сечение этой поверхности по биссектрисе  D₁ОD₂   угла. Кривая  получена при  p₁=0.6 и p₂ =0.4. При этом функция Э является неоднозначной. На практике эту неоднозначность можно обойти, ограничившись изменением достоверностей в интервале [0.5;1], определяющем рабочую область. Как видно из рисунка 2.2.2 в рабочей (заштрихованной) области количество информации увеличивается с увеличением достоверностей.

 

Рисунок 2.2.2 - Сечение поверхности информационного критерия (D₁=D₂).

Именно в этой области экстремальные значения параметров обучения, соответствующие максимуму критерия, являются оптимальными в информационном смысле.

 На практике точностные характеристики заменяются эмпирическими частотами. Для двухальтернативного решения введём следующие оценки точностных характеристик:

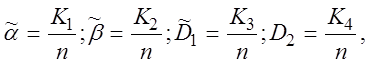                                                              (2.2.16)

где  K₁ и  K₃ число событий, заключающийся в нахождении значения параметра вне поля допусков и в поле допусков соответственно при условии, что истинное значение параметра находится в поле допусков; K₂  и K₄ - число событий, заключающихся в нахождении измеренного значения параметра в поле допусков и вне поля допусков соответственно при условии, что истинное значение параметра находится вне поля допусков; n - число испытаний. На основании (2.2.15) с учетом (2.2.16) формула (2.2.4) примет вид:

            Э_I=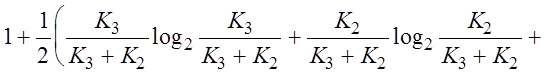

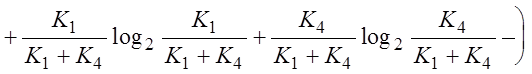            .                          (2.2.17)

Таким образом, информационный критерий (2.2.17), являясь функционалом точностных характеристик, прямо характеризует эффективность функционирования СППР в зависимости от нахождения контролируемых параметров (признаков) в своих эксплуатационных и контрольных допусках.

Для нахождения максимального значения критерия Э, строится гиперсфера с центром в вершине эталонного вектора для текущего класса, радиус d которой увеличивается от 0 до тех пор, пока текущее значение Э, не станет меньше его предыдущего значения. Для каждого значения d вычисляется расстояние (путем сложения по модулю 2) между эталонным вектором и каждой реализацией для текущего класса, а также для класса, ближайшего к текущему. В зависимости от значения кодового расстояния, получает приращение один из коэффициентов К1, К2, К3, K4 (для ближайшего к текущему класса). После определения этих коэффициентов вычисляется Э, по формуле (2.2.17). В случае, если текущее значение Э меньше предыдущего (Эдред), Эдред считается максимальным значением информационного критерия. В противном случае вычисления повторяются для радиуса, увеличенного на единицу. Значение d, соответствующее наибольшему Э, является радиусом разделяющей гиперповерхности для данного класса.

Однако существуют ситуации, в которых максимальное значение критерия является неинформативным, например, нахождение максимально удалённого в информационном смысле  класса. В таких случаях используется площадь рабочей области критерия. Алгоритм её вычисления схож с алгоритмом нахождения максимального значения с той разницей, что производится суммирование всех значений критерия в рабочей  области.