Оценка функциональной эффективности классификации состояний

2.2 Оценка функциональной эффективности классификации состояний.

В рамках теоретико-множественного подхода понятие система детализируется как комплекс способов, образующих определенную структуру, предназначенную для достижения поставленной цели с требуемой эффективностью.

Поскольку формирование критерия эффективности направлено на снятие неопределенности, то критерий имеет информационную природу. Осуществить на практике полную формализацию цели не удается из-за неполноты априорной информации. Поэтому критерий задается, как правило, содержательно в виде обобщенных интегральных характеристик (экологических, экономических, массогабаритных, функциональных, метрологических и т.д.). При этом на область существования системы накладываются ограничения, в результате которых она “сужается” до допустимой области.

Задача выбора и вычисления КФЭ является центральной проблемой оценивания функциональной эффективности сложных систем. Можно выделить два основных подхода к оцениванию, один из которых основан на экономических показателях, а другой на информационных. Промежуточным является подход, базирующийся на обобщенном КФЭ, учитывающем как экономические затраты, так и количественные информационные и другие характеристики системы (например, динамические,  массогабаритные, надежностные, энергетические).

КФЭ сложной системы с учетом специфики СППР  должен отвечать следующим основным требованиям:

-быть, по возможности, прямым, а не косвенным;

-быть физичным, математически вычисляемым и иметь геометрический смысл;

-быть количественным и выражаться одним числом, характеризующим степень соответствия системы своему назначению;

-носить конструктивный  характер, т.е. позволять разрабатывать методы анализа и синтеза СППР;

-быть универсальным, т.е. пригодным для использования в СППР широкого назначения;

-быть чувствительным к изменению параметров н характеристик СППР;

-позволять оптимизировать процесс обучения в смысле его оперативности и достоверности распознавания на экзамене;

-зависеть от точностных характеристик СППР.

 Всем этим требованиям удовлетворяют критерии, характеризующие информационную способность системы.

В данной работе для автонастройки сложной системы в качестве критерия оценки функциональной эффективности классификации состояний используется информационный критерий вида [3,4]:

                       Э_I =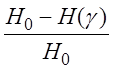,                                                                       (2.2.1)

где                            H₀ = -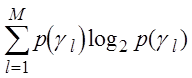                                                (2.2.2)

- априорная (безусловная) энтропия;

  H(g)=-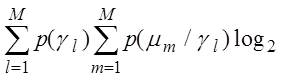,                                               (2.2.3)                                                                                                        

- условная энтропия, характеризующая неопределенность принятия решения, где p( g_e  ) – априорная вероятность принятия гипотезы, p(m_m  /  g_e) - апостериорная условная вероятность того, что имеет место событие m_m при   условии принятия гипотезы g_e   ;  M - число альтернативных гипотез.

Применение критерия (2.2.1) для оценки эффективности функционирования сложных систем представляется естественным и наиболее полно отражающим их информационную природу. 

На практике при оценивании функциональной эффективности  имеют место следующие реальные допущения:

-не учитываются затраты на получение и обработку информации;

-решение является двухальтернативным   (M=2);

-для реальной СППР априорная информация является неполной, поэтому оправдано принятие равновероятных гипотез:  p(g ₁) = p(g ₂) = 0.5;

-при каждом испытании осуществляется одношаговая процедура принятия решения.

 Тогда критерий (2.2.1) принимает простой частный вид:

            Э_{I 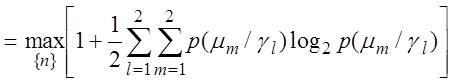,}                                     (2.2.4)

Критерий (2.2.4) в полной мере удовлетворяет сформированным выше требованиям к КФЭ.

При двухальтернативной системе оценок решений, например, при допусковом контроле в форме "В НОРМЕ" - "НЕ В НОРМЕ" в качестве основной гипотезы примем гипотезу о нахождении измеренного значения контролируемого параметра в поле допусков и в качестве альтернативной гипотезы - гипотезу о нахождении измеренного значения параметра не в поле допусков. При этом, имеют место четыре возможных исхода процесса контроля, характеризующиеся следующими вероятностями - точностными характеристиками:

- ошибка первого рода (Рисунок 2.2.1а); условная вероятность того, что измерянное значение лежит вне поля допуска при условии, что истинное значение принадлежит полю допуска: 

                       a = p( xÎ d / z Îd );                                                            (2.2.5)

- ошибка второго рода (Рисунок 2.4.1б); условная вероятность того, что измерянное значение лежит в поле допуска при условии, что истинное значение не принадлежит полю допуска:

                       b = p( xÎ d / z Îd );                                                              (2.2.6)

 - первая достоверность (Рисунок 2.4.1в); условная вероятность того, что измерянное значение лежит в поле допуска при условии, что истинное значение также принадлежит полю допуска:

                       D₁ = p( xÎ d / z Îd );                                                             (2.2.7)

- и вторая достоверность (Рисунок 2.2.1г); условная вероятность того, что измерянное значение лежит вне поля допуска при условии, что истинное значение также не принадлежит полю допуска: