


2. Опис змінних та функцій програми,математичний розв’язок.
2.1 Опис змінних та функцій програми.
1) xi, yi- координати і-ої точки на дузі;
2) sxi, syi- сума координат;
3) Xc,Yc- координати центра ваги;
4) t-параметр, що відповідає φ в (12)-(13);
5) dt-крок зміни t;
6) n- кількість кроків (точок розбиття).
Решта змінних є службовими, і використовуються для проміжних розрахунків, полегшення написання програми, тощо. Наприклад, змінні х0 і у0 мають відповідні значення координат початку координат на екрані, і при бажанні можуть бути змінені.
7) grafic_Х – функція, що рисує графік залежності центра ваги від координат;
8) titul - функція, що виводить титульний листок;
9) vikno - функція, що створює вікно ( при розрахунку центра ваги).
2.2 Математичний розв’язок
Центр ваги
твердого тіла ─ це точка, яка визначається радіус-вектором ![]() , що знаходиться за формулою:
, що знаходиться за формулою:
![]() =
= 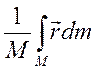 ,
(1)
,
(1)
де М ─
маса твердого тіла, ![]() ─ радіус-вектор, проведений із
початку відліку в довільну точку твердого тіла.
─ радіус-вектор, проведений із
початку відліку в довільну точку твердого тіла.
Фактично,
знайшовши вектор ![]() (його координати), ми знайдемо
координати центру ваги твердого тіла, оскільки координати вектора знаходяться
як різниця координат кінцевої і початкової точок, а в нашому випадку кінцева
точка ─ це є центр ваги, а початкова ─ початок відліку О(0;0;0).
(його координати), ми знайдемо
координати центру ваги твердого тіла, оскільки координати вектора знаходяться
як різниця координат кінцевої і початкової точок, а в нашому випадку кінцева
точка ─ це є центр ваги, а початкова ─ початок відліку О(0;0;0).
Розпишемо
радіус-вектори ![]() і
і ![]() у
вигляді:
у
вигляді:
![]() =
= ![]()
![]() +
+![]()
![]() ,
(2)
,
(2)
![]() =
= ![]()
![]() +
+![]()
![]() ,
(3)
,
(3)
де ![]() ,
, ![]() ─ це
орти відповідно осей ox і oy;
─ це
орти відповідно осей ox і oy; ![]() ,
, ![]() ─
координати довільної точки твердого тіла;
─
координати довільної точки твердого тіла; ![]() ,
, ![]() , ─ координати центру ваги твердого тіла.
, ─ координати центру ваги твердого тіла.
Підставимо (2) і (3) в (1):
![]()
![]() +
+![]()
![]() + =
+ = 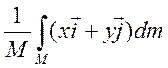 ,
(4)
,
(4)
Розбиваємо в останньому виразі інтеграл справа в (4) на два інтеграли:
![]()
![]() +
+![]()
![]() = (
= (![]()
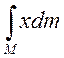 )
)![]() + (
+ (![]()
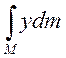 )
)![]() (5)
(5)
Із (5) випливає, що задача знаходження координат центру ваги твердого тіла звелась до знаходження інтегралів справа в (5). Використовуючи властивості інтеграла, можна перейти до додавання:
![]() =
=![]()
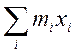 ,
(6)
,
(6)
![]() =
=![]()
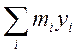 ,
(7)
,
(7)
Де хі, уі − координати точки масою mi (уі+1-уі→0, хі+1-хі→0).
Додатково покладаючи, що
![]() ,
(8)
,
(8)
і, враховуючи, що
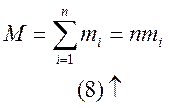 (9)
(9)
отримуємо:
![]() =
=![]()
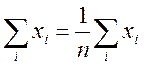 ,
(10)
,
(10)
![]() =
=![]()
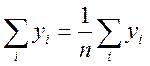 ,
(11)
,
(11)
Іншими словами, центр мас можна знайти, використовуючи формули (10)−(11), взявши за уі та хі точки, що розподілені рівномірно по всій довжині дуги, на достатньо малій відстані. На практиці це реалізується, наприклад, переходом до полярних координат:
![]() =
=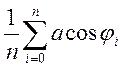 ,
(12)
,
(12)
![]() =
=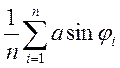 ,
(13)
,
(13)
де ![]()
Формули (12)−(13) і є розрахунковими для даної задачі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.