Методы расчета линейных цепей в стационарных режимах, страница 2

         -I₁₀+I_k5+I₉=0;

         I₁₀=I_k5+I₉=1,5+0,48=1,98 A.

Найдем токи I₁₁, I₁₂:

         I₁₁=I₅=0,3 A.

По первому закону Кирхгофа найдем ток I₁₂:

         I₁₁+I₁₂-I_k5=0;

         I₁₂=I_k5-I₁₁=1,5-0,3=1,2 A.

Токи I₁=I₂=I^*₂=0,18 A и ток I₁₅=I₄=0,148 A.

5.Составить баланс мощности в преобразованной цепи, вычислить отдельную суммарную мощность источников и суммарную мощность потребителей.

         ∑P_{потреб.}=∑P_источ.

∑P_{потреб.}=I₁²*R_6,7,8+I₂²*R_1,2+I₃²*R_9,10+I₄²*R₁₅+I₅²*R_11,12+I₆²*R_3,4,5=

=(-0,628)²*60+(-0,18)²*80+(-0,48)²*100+(0,148)²*80+(-0,3)²*80+

+(0,448)²*90=76,31 Вт.

∑P_источ.=I₃*E₁₀+I₅*E₁₁+I₆*E_2,3=0,48*100-0,3*40+0,448*90=48-

-12+40,32=76,32 Вт.

6.Рассчитать токи в преобразованной цепи методом узловых потенциалов, заземлив центральный узел цепи.

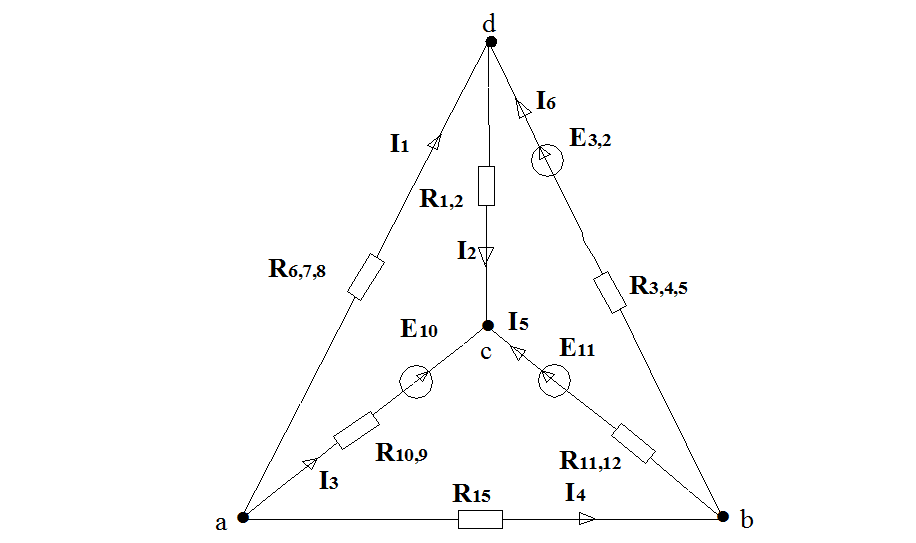
            Примем узел φ_с равным нулю тогда:

         φ_с=0;

G_aaφ_a+G_abφ_b+G_adφ_d=I_a

         G_baφ_a+G_bbφ_b+G_bdφ_d=I_b

              G_daφ_a+G_dbφ_b+G_ddφ_d=I_d

Найдем собственные проводимости узлов a, b, d:

         G_aa=1/R_6,7,8+1/R_9,10+1/R₁₅=1/60+1/100+1/80= 0,0385 Ом.

         G_bb=1/R_3,4,5+1/R_11,12+1/R₁₅=1/90+1/80+1/80= 0,036 Ом.

         G_dd=1/R_6,7,8+1/R_1,2+1/R_3,4,5=1/60+1/80+1/90= 0,0395 Ом.

Найдем взаимные проводимости:

         G_ab=G_ba= -1/R₁₅= -1/80= -0,0125 Ом.

         G_ad=G_da= -1/R_6,7,8= -1/60= -0,016 Ом.

         G_bd=G_db= -1/R_3,4,5= -1/90= -0,011 Ом.

Найдем узловые токи:

         I_aa= -E₁₀/R_9,10= -100/100= -1 A.

         I_bb= -E₁₁/R_11,12-E_2,3/R_3,4,5= -40/80-90/90= -1,5 A.

         I_dd= E_2,3/R_3,4,5= 90/90= 1A.

Запишем систему с известными значениями:

         0,0385φ_a-0,0125φ_b-0,016φ_d= -1

         -0,0125φ_a+0,036φ_b-0,011φ_d= -1,5

         -0,016φ_a-0,011φ_b+0,0395φ_d= 1

Составим четыре матрицы и найдем определители этих матриц для нахождения соответственно узловых потенциалов φ_a, φ_b, φ_d.

         φ_a=x₁/∆x, φ_b=x₂/∆x, φ_d=x₃/∆x;

         0,0385  -0,0125  -0,016

∆x=  -0,0125  0,036   -0,011       =0,0000304

         -0,016   -0,011   0,0395

           -1    -0,0125  -0,016

x₁=    -1,5   0,036   -0,011       = -0,00159

            1    -0,011   0,0395

         0,0385      -1      -0,016

x₂=   -0,0125   -1,5     -0,011       = -0,00149

         -0,016        1      0,0395

 

         0,0385  -0,0125     -1

x₃=   -0,0125  0,036     -1,5       = -0,00042

         -0,016   -0,011        1

Найдем φ_a, φ_b, φ_d:

         φ_a=x₁/∆x= -0,00159/0,0000304= -52,302 В.

         φ_b=x₂/∆x= -0,00149/0,0000304= -63,82 В.

         φ_d=x₃/∆x= -0,00042/0,0000304= -13,82 В.

Найдем токи I:

         I₁= φ_a- φ_d/R_6,7,8= -52,302+13,82/60= -0,641 A.

         I₂= φ_d- φ_c/R_1,2= -13,82/80= -0,172 A.

         I₃= φ_a- φ_c+E₁₀/R_9,10= -52,302+100/100= 0,476 A.

         I₄= φ_a- φ_b/R₁₅= -52,302+63,82/80= 0,143 A.

         I₅= φ_b- φ_c+E₁₁/R_11,12= -63,82+40/80= -0,297 A.

         I₆= φ_b- φ_d+E_2,3/R_3,4,5= -63,82+13,82+90/90= 0,444 A.    

7. Рассчитать и начертить потенциальную диаграмму для любого замкнутого контура, включающего два ЭДС.

8. Результаты работы по пунктам 3 и 6 свести в таблице и сравнить их между собой.

№	I1, A	I2, A	I3, A	I4, A	I5, A	I6, A
п. 3	-0,628	-0,18	-0,48	0,148	-0,3	0,448
п. 6	-0,641	-0,172	0,476	0,143	-0,297	0,444

Рассчитать ток в ветви с резистором R₁ и R₂ методом эквивалентного генератора.

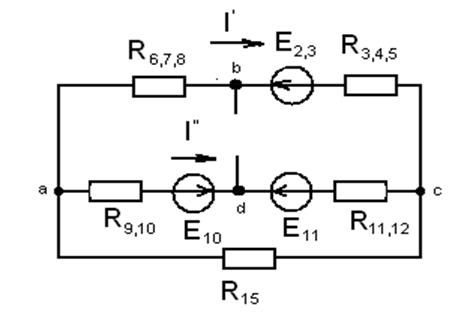
         Запишем формулу для нахождения тока I₂ методом эквивалентного генератора: I₂=E_э/R_1,2+R_э.

         Найдем методом узловых потенциалов токи I’ и I” для того чтобы найти U_b,d=E_э=φ_b- φ_d=I”R_9,10-I’R_6,7,8-E₁₀.

         Приймем   φ_a =0

                  G_cc φ_c=I_cc

         Найдем собственную проводимость узла с:

         G_cc=1/R_6,7,8+R_3,4,5+1/R_9,10+R_11,12+1/R₁₅=1/150+1/180+1/80=

= 0,0066+0,0055+0,0125=0,0246 Ом.

         Найдем узловой ток:

                  I_cc=(-E_2,3/ R_6,7,8)+(R_3,4,5+E₁₀-E₁₁/ R_9,10+R_11,12)=(-90/60+90)+( 100-40/100+80)=-0,6+0,3=-0,3 A.

         Найдем потенциал узла с:

                  φ _c=I_cc/G_cc=-0,3/0,0246=-12,2 В.

         Найдем токи I’ и I”:

               I’= φ_a- φ_c-E_2,3/R_6,7,8+R_3,4,5=12,2-90/60+90=-0,518 A.

               I”=φ_a-φ_c+E₁₀-E₁₁/R_9,10+R_11,12=12,2+(100-40)/100+80=0,401A

               φ_b= φ_d-E₁₀+I”R_9,10-I’R_6,7,8

         Найдем U_b,d=E_э:

               E_э= φ_b- φ_d=I”R_9,10-I’R_6,7,8-E₁₀=0,401*100+0,518*60-100 = =40,1 + 31,08 – 100= - 28,82 В.

         Приобразуем схему и найдем R_э:      

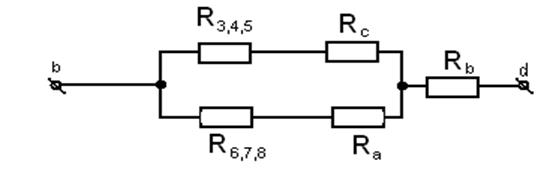
         Найдем сопротивления R_a, R_b, R_c в преобразованной цепи:

                  R’=R_9,10+R_11,12+R₁₅=100+80+80=260 Ом.

                  R_a=R_9,10*R₁₅/R’=8000/260=30,76 Ом.

                  R_b=R_9,10*R_11,12/R’=8000/260=30,76 Ом.

                  R_c=R_11,12*R₁₅/R’=6400/260=24,61 Ом.

         Найдем R_э:

                  R_э=((R_6,7,8+R_a)*(R_3,4,5+R_c)/ R_6,7,8+R_a +  R_3,4,5 + R_c ) + R_b = ((60+30,76)*(90+24,61)/60+30,76+90+24,61)+30,76=50,65+30,76=

=81,41 Ом.

         Найдем ток I₂:

                  I₂=E_э/R_1,2+R_э=-28,82/80+81,41=-28,82/161,41=-0,179 A.