Основною метою статистичної обробки при розвідувальному аналізі даних є оцінка статистичної сталості та статистичної однорідності вхідної вибіркової послідовності. Під оцінкою статистичної сталості вибіркової послідовності розуміється підтвердження статистичної гіпотези про незмінність емпіричного розподілу та його параметрів. Оцінка статистичної однорідності вибіркової послідовності дозволяє або виявити окремі ознаки розпізнавання, які не є випадковими, або, взагалі, поставити під сумнів випадковість всієї послідовності. Перехід випадкових ознак розпізнавання у невипадкові в задачах контролю та управління може бути обумовлений як виходом їх значень за свої експлуатаційні (нормовані) поля допусків, наприклад, через поступові відмови в СППР, так і через невдалий вибір рандомізуючої системи контрольних допусків на ознаки розпізнавння, внаслідок чого ймовірність знаходження відповідної ознаки в своїх контрольних допусках може набувати близьких до нуля або одиниці значень. В КАД оцінка статистичної однородності вхідної послідовності даних набуває особливої актуальності, оскільки дозволяє визначити величину відхилення поточного показника однорідності від попереднього. Тоді шляхом порівняння знайденої величини відхилення з її пороговим значенням можна встановити момент переходу ОК із одного функціонального стану в інший і саме цим ідентифікувати належність вхідної послідовності до нового класу розпізнавання. Зрозуміло, що тут мова може йти тільки про інтервальну оцінку момента зміни функціонального стану ОК з відповідним рівнем довіри.
Сьома
задача набуває важливого значення при
класифікаційному аналізі з відкритим алфавітом класів розпізнавання ![]() ^, який поповнюється або в процесі
навчання, або при виявленні нових класів у режимі самонавчання СППР.
Особливість цієї задачі в КАД полягає в тому, що її розв’язання дозволяє не
тільки оцінювати точнісні характеристики процесу навчання, які
визначають асимптотичну точність СППР, а й безпосередньо змінювати алгоритм
навчання з метою цілеспрямованого збільшення надлишковості вибіркових
послідовностей у міру введення нових класів алфавіту
^, який поповнюється або в процесі
навчання, або при виявленні нових класів у режимі самонавчання СППР.
Особливість цієї задачі в КАД полягає в тому, що її розв’язання дозволяє не
тільки оцінювати точнісні характеристики процесу навчання, які
визначають асимптотичну точність СППР, а й безпосередньо змінювати алгоритм
навчання з метою цілеспрямованого збільшення надлишковості вибіркових
послідовностей у міру введення нових класів алфавіту![]() ^.
Розв’язання цієї задачі тісно
пов’язано із застосуванням методів та ідей теорії
завадозахищеного кодування [10,15 ]. Крім того, для одержання оцінок
допустимих співвідношень між геометричними параметрами РГП класів розпізнавання
та розмірністю простору ознак важливого значення набуває розробка теорії
упакування такого простору геометричними тілами, наприклад, гіперсферами з
різними діаметрами. При цьому актуальним є розгляд укладок як недеформованих
гіперсфер (випадок прийняття гіпотези чіткої компактності реалізацій образу,
коли класи не перетинаються), так і деформованих гіперсфер (випадок нечіткої
компактності, яка обумовлює перетинність класів).
^.
Розв’язання цієї задачі тісно
пов’язано із застосуванням методів та ідей теорії
завадозахищеного кодування [10,15 ]. Крім того, для одержання оцінок
допустимих співвідношень між геометричними параметрами РГП класів розпізнавання
та розмірністю простору ознак важливого значення набуває розробка теорії
упакування такого простору геометричними тілами, наприклад, гіперсферами з
різними діаметрами. При цьому актуальним є розгляд укладок як недеформованих
гіперсфер (випадок прийняття гіпотези чіткої компактності реалізацій образу,
коли класи не перетинаються), так і деформованих гіперсфер (випадок нечіткої
компактності, яка обумовлює перетинність класів).
Розв’язання
восьмої задачі спрямовано на підтримку функціональної ефективності СППР
на належному рівні. У КАД, поряд з постановленням задачі
прогнозування зміни функціонального
стану (або інформаційної здатності) системи, існує
також специфічна задача – це
визначення моменту перенавчання СППР. Необхідність перенавчання СППР обумовлена
дрейфом у часі та в просторі
ознак W вершин випадкових векторів – реалізацій образів, а отже, й
вершин еталонних векторів при незмінних геометричних параметрах РГП відповідних
класів ![]() ,
які сформрвано на етапі навчання системи.
Одним із можливих шляхів розв’язання цієї задачі є
конструювання прогнозувальної функції у вигляді одновимірної
порядкової статистики, яка чутлива до виходу значень ознак
розпізнавання за межі своїх контрольних допусків. Тоді прогнозування
моменту перенавчання СППР може здійснюватися через оцінку виходу поточної
статистики
,
які сформрвано на етапі навчання системи.
Одним із можливих шляхів розв’язання цієї задачі є
конструювання прогнозувальної функції у вигляді одновимірної
порядкової статистики, яка чутлива до виходу значень ознак
розпізнавання за межі своїх контрольних допусків. Тоді прогнозування
моменту перенавчання СППР може здійснюватися через оцінку виходу поточної
статистики ![]() , що
обчислюється на екзамені, за межі системи довірчих інтервалів
для значення відповідної екстремальної порядкової статистики
, що
обчислюється на екзамені, за межі системи довірчих інтервалів
для значення відповідної екстремальної порядкової статистики ![]() , що обчислюється на етапі прогностичного
навчання і відповідає максимуму
, що обчислюється на етапі прогностичного
навчання і відповідає максимуму ![]() КФЕ розпізнавання
класу
КФЕ розпізнавання
класу ![]() .
.
Оскільки зміна функціонального стану СППР призводить до зміни її точнісних характеристик, то взагалі мова тут може йти про зміну інформаційної здатності системи, яка оцінюється усередненим значенням КФЕ, який є часовою функцією. Тоді в загальному випадку умовою перенавчання СППР є виконання такого співвідношення:
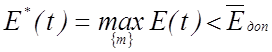 ,
,
де
![]() - допустиме мінімальне усереднене значення КФЕ СППР.
- допустиме мінімальне усереднене значення КФЕ СППР.
Безумовно, кількість типових задач КАД, наведених вище, не є повною. Відбувається невпинне формування нових задач, їх диференціація і з’являються нові області їх застосування [ ].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.