Языки моделирования и описания цифровой аппаратуры, страница 6

Третий путь – создание автономного ЯМ самый трудоёмкий, так как требует разработки собственного компилятора. Однако он и самый перспективный, потому что не ограничивает разработчика рамками уже существующего базового языка. Именно этот путь был выбран при создании наиболее мощного, эффективного и универсального языка моделирования и описания аппаратуры VHDL, принятого ныне в качестве неофициального мирового стандарта.

Рассмотрим несколько примеров наиболее популярных языков моделирования. Более подробно они будут обсуждаться в третьей теме, а здесь мы собираемся получить только «общее впечатление».

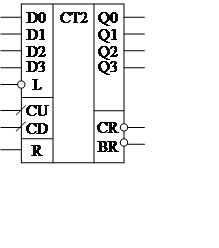
В качестве объекта описания возьмём двоичный реверсивный счётчик 555ИЕ7,графическое изображение которого показано справа. Напомним, что он имеет четыре режима работы: асинхронный сброс (наиболее приоритетная команда), асинхронная параллельная загрузка, счёт на увеличение (счёт вверх) и счёт на уменьшение (счёт вниз).

На рис.3 приведена его модель, построенная с помощью языка моделирования PML пакета автоматизированного проектирования PCAD.

555IE7()

INPUT D0,D1,D2,D3,L,CU,CD,R;

OUTPUT Q0,Q1,Q2,Q3,CR,BR;

LOCAL Q[4];

{

IF (R=="1") Q="0x0" (2,2,"D","D");                                                      /* сброс          */

ELSE

{ IF (L=="0")                                Q=[D3,D2,D1,D0]   (4,4,"D","D");   /* загрузка     */

   IF (L=="1")&&(CU=="/")        Q=Q+"0X1"             (8,8,"D","D");   /* счёт вверх */

   IF (L=="1")&&(CD=="/")        Q=Q+"0XF"            (8,8,"D","D");   /* счёт вниз   */

}

CR=~(Q[0]&Q[1]&Q[2]&Q[3]&~CU)                         (8,10,"D","D");

BR=~(~Q[0]&~Q[1]&~Q[2]&~Q[3]&~CD)                (8,10,"D","D");

Q0=Q[0] (0,2,"D","D");

Q1=Q[1];

Q2=Q[2];

Q3=Q[3];

}

Рис.3. PML-модель двоичного реверсивного счётчика 555IE7

Структура PML-модели состоит из двух частей. Первая часть (раздел описания) содержит заголовок модели и описание внешних входных и выходных сигналов. Здесь же вслед за ключевым словом LOCAL можно объявить локальную переменную или внутреннюю шину, как в нашем примере: Q[4]. Они используются для хранения текущего состояния моделируемого компонента.

Вторая часть модели (исполняемый раздел) заключена в фигурные скобки и содержит набор исполняемых операторов. В конце каждого оператора может присутствовать необязательный PCL-список, заключённый в круглые скобки. В нём указываются задержки переключения выхода из 0 в 1 и в обратном направлении.

Например, в режиме параллельной загрузки (L=="0") задержка срабатывания выходов Q0…Q3 составит 4 условные единицы времени. В PCAD’е по умолчанию условная единица равна 1нс. Если PCL-список отсутствует, то задержка принимается равной 1нс.

Два последних параметра в PCL-списке задают логическую силу выхода, косвенно отражающую его нагрузочную способность. В пакете PCAD существуют четыре уровня логической силы: S, D, R, Z. Они перечислены в порядке убывания. Выход с силой S – самый мощный. Этот простой механизм оказывается достаточным для разрешения конфликтов на шинах.

Язык PML не имеет внешней шины, поэтому при выдаче результатов приходится внутреннюю шину преобразовывать в соответствующее число одиночных узлов (проводников). В нашем примере шина Q[4] «раскладывается» на четыре одиночных сигнала Q0…Q3. Это делается с помощью последних четырёх операторов присваивания.

Для демонстрации возможностей языка PML первому из них приписан PCL-список:

Q0=Q[0] (0,2,"D","D");

Указанные в нём задержки будут просуммированы с теми, что указаны при вычислении шинного сигнала. Например, при параллельной загрузке данных суммарная задержка при переключении выхода Q0 вверх составит 4нс (4нс+0нс), а переключение вниз будет осуществляться с задержкой 6нс (4нс+2нс).