Как считают кибернетики? Двоичная система счисления, страница 3

Найдем для примера двоичное дополнение числа 101₂. Действуем по инструкции. Двоичным дополнением будет число 11₂.

Для числа 1010₂ двоичным дополнением будет число 110₂.

Для следующих двоичных чисел найди двоичные дополнения сам:

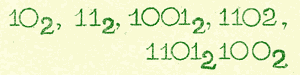
После этих предварительных объяснений переходим к изучению вычитания с помощью двоичного дополнения числа.

Пусть из числа 1101₂ следует вычесть число 1011₂. Вычисления проводим по схеме:

1. Находим двоичное дополнение вычитаемого. Это будет число 101₂.

2. Затем к данному уменьшаемому прибавляем найденное двоичное дополнение: 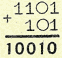и из полученной суммы вычитаем число 10 000₂.
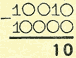это и есть ответ (искомая разность).

Еще пример:

1. Находим двоичное дополнение вычитаемого 1012. Это число 112.

2. Складываем уменьшаемое и найденное двоичное дополнение: 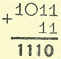из полученной суммы вычитаем число 1000₂: 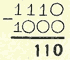это и есть разность.

Попробуй следующие примеры сделать самостоятельно:

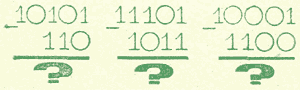
Примеры выполняй внимательно и обязательно сделай проверку.

Как ты думаешь: следует ли пользоваться двоичным дополнением числа, если вычитаемыми являются числа типа: 10₂, 100₂, 1000₂ и т. д.?

ДЕЛИТЬ ПОМОГАЕТ ВЫЧИТАНИЕ

Для деления а двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать.
Приведем такой пример:

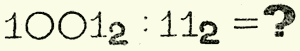
Располагаем данные числа, как при обычном делении, углом:

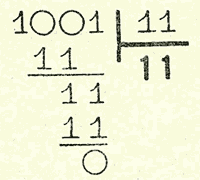
Перед началом вычисления нам пришлось сравнить 10 и 11. Заметив, что 10 меньше, чем 11, мы перешли к числу 100, которое также сравнили с числом 11. 100 больше, чем 11. Затем вычли 11 из 100 и т. д.

Еще несколько примеров:

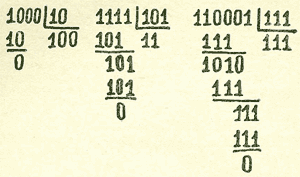
Предлагаем несколько примеров для тренировки:

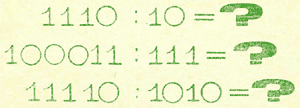
Но тебе, наверное, известно, что деление можно заменить вычитанием. Что значит 30 разделить на 3? Это значит выяснить, сколько раз 3 содержится в 30. А это можно сделать и вычитая тройки из 30. Отнимем одну тройку, вторую, третью и так до последней. Количество отнятых троек и будет частным.

Если попробуем деление заменить вычитанием, то здесь нам и понадобится вычитание с помощью двоичных дополнений.

Позже ты узнаешь, что в вычислительных машинах деление действительно заменяется вычитанием, которое проводится с привлечением двоичного дополнения.

На этом мы завершаем ознакомление с тем, как считают в кибернетике. Это очень краткое знакомство: мы познакомились лишь с одной недесятичной арифметикой (двоичной), а в кибернетике используются и другие недесятичные системы счисления— например, система с основанием, равным 8.

Рекомендуем продолжить расширение своих знаний о системах счисления, книги указаны в конце нашей «Азбуки».

РАССКАЗ КИБЫ

Я давно знаком с юными любителями кибернетики из Малой академии наук школьников Крыма «Искатель», бывал у них на занятиях школы юных кибернетиков — знакомился с изготовленными у них моделями,

Все сам видел, включал и выключал — можете верить!