Как считают кибернетики? Двоичная система счисления, страница 2

Если сложение в двоичной системе усвоено хорошо, можно переходить к умножению. Вот таблица:

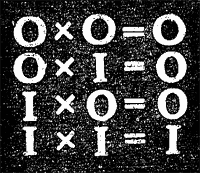
Научиться умножать нужно самому.

Рассмотри внимательно решенные примеры — это поможет тебе сообразить, как проводилось умножение:

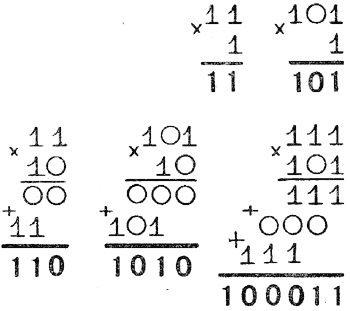
Умножение на «О» в двоичной системе проводится так же, как и в десятичной. Строки нолей приведены для наглядности.

Следующие примеры попробуй сделать самостоятельно:

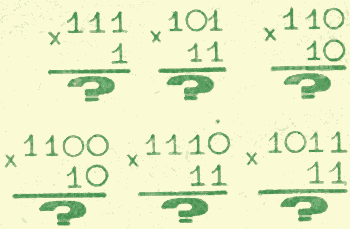
Проверь  свои  вычисления,  записав  все  примеры в десятичной системе счисления.

Упражнения на внимательность

В данных примерах восстанови пропущенные цифры, поставь их вместо знака «?» и проверь себя:

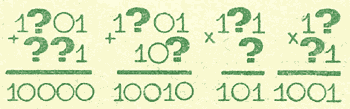
ВЫЧИТАНИЕ ТРЕБУЕТ БОЛЬШЕ ВНИМАНИЯ

Перед знакомством со следующим действием — вычитанием — постарайся правильно определить, какое из чисел в каждой паре больше другого:

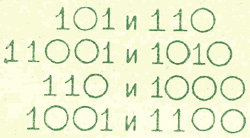
Начинай сравнение со старших разрядов. Найди среди чисел самое большое, самое малое и среднее по величине:

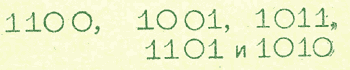
Еще одно упражнение:

Вместо знака «?» поставь «1» или «0» так, чтобы полученное число было больше другого:

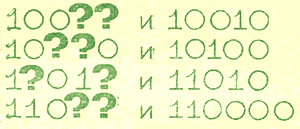
Ответов может быть несколько.

Познакомься, как следует проводить вычитание:

Как видишь, это не очень просто. Будь внимателен. Все примеры проверь сложением.

А эти примеры реши сам:

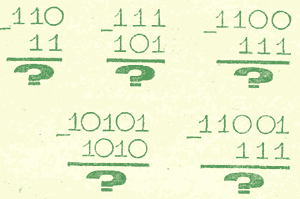
Вычитание и в десятичной системе — одно из трудных действий, поэтому вычислители всегда старались как-нибудь упростить эту работу.
Познакомься еще с одним способом вычитания.

Ты, наверное, согласишься, что в десятичной системе вычесть десятку или сотню легче, нежели какое-нибудь не круглое число — например, 9 или 57. Эти числа вычитать труднее.

Легче нам и вычитать из десятка и из сотни. Такие удобства используются в устном счете давно.

Введем новое понятие «десятичное дополнение числа» — разность между 10 или 100 и данным числом. Так, десятичным дополнением числа 7 является число 3, ведь 3=10— 7.

Десятичным дополнением числа 27 будет число 73, ибо 73=100 — 27.

Когда мы находим десятичное дополнение, мы вычитаем из десятка, сотни или тысячи, а это делать нетрудно.

Десятичное дополнение введено для того, чтобы облегчить вычитание.

Пример: Нужно от 12 отнять 7. Сделаем это так: сначала найдем десятичное дополнение вычитаемого (7). Это число 3 (10—7 = 3). Последующие вычисления располагаем так: 12 + 3—10, то есть сначала к 12 прибавляем 3 и затем из суммы вычитаем 10.

Ты, наверное, обратил внимание, что мы один раз вычли из десяти и один раз вычли десять. Вычитаний других чисел не было. Действия вычитания проводились в данном примере только с десятками. В этом преимущество этого способа.

Пользуясь десятичным дополнением вычитаемого, выполни следующие упражнения:

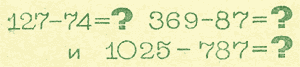
Проверь себя — хорошо ли ты все понял. Не жалей времени, прочти еще раз. Это важный раздел.

Вернемся к вычитанию в двоичной системе счисления. Введем понятие о «двоичном дополнении числа».

Двоичное дополнение числа находится по такой инструкции: