Непрерывные цепи Маркова как модель эволюции систем. Уравнения Колмогорова

71. Непрерывные цепи Маркова как модель эволюции систем. Уравнения Колмогорова.

Опр. Если переход из одного состояния в другое осуществляется скачком в случайный момент времени, то последовательность переходов описывается Марковским случайным процессом с непрерывным временем.

Для решения задач анализа и проектирования вводят понятие состояния, во вторых указываются все состояния в которых может находится система, в третьих составляется граф состояний системы, в четвертых указывается в каком состоянии находится система в начальный момент времени, в пятых для каждого возможного перехода указывается соответствующая интенсивность.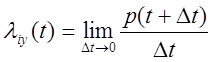

l_iy(t) – плотность вероятности

p(t+Dt) – вероятность того, что событие произойдет на интервале Dt

Если l_iy не является функцией времени, то непрерывные цепи Маркова являются однородными. Системы описываемые непрерывными цепями Маркова, называют иногда Пуассоновскими, так как для того чтобы процесс перехода был Марковским необходимо, чтобы входящий поток событий, который переводит систему из одного состояния в другое был бы простейшим Пуассоновским. Основное преимущество этих систем заключается в том, что они описываются с помощью линейных ДУ, которые составлены относительно вероятности состояния системы.

P₁(t+Dt) = P₁(t)*(1-l₁₂Dt)+P₂(t) l₂₁Dt

P₂(t+Dt)

P(a) – вероятность того, что система находится в состоянии S₁ и осталась в нем же

P(a)=P₁(t)(1-l₁₂Dt)

P(б)=P₂(t) l₂₁Dt – была в S₂

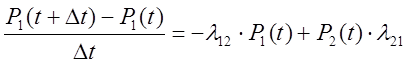
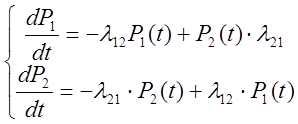- система ДУ Колмогорова

P₁(t)+P₂(t)=1

P₁ – среднее относительное время пребывания системы в состоянии 1.

Финальные или предельные вероятности имеют постоянные значения

Правило составления уравнений Колмогорова

            Если система представлена в виде графа, то для записи уравнений Колмогорова можно воспользоваться следующим правилом: производная  вероятности пребывания системы в состоянии S_i равна алгебраической сумме нескольких членов. Количество членов этой суммы равно числу дуг графа входящих и выходящих из вершины S_i. Если дуга направлена в состояние S_i, то член суммы берется со знаком ‘+’, если дуга выходит из состояния S_i, то со знаком ‘-‘. Каждый член суммы равен произведению вероятности того состояния из которого исходит дуга на интенсивность потока событий переводящего систему по данной дуге.