



Детали, необходимые для работы цеха, находятся на цеховом и центральном складах. На цеховом складе хранится 20 комплектов деталей, потребность в которых возникает через 60±10 мин и составляет один комплект. В случае снижения запасов до трех комплектов формируется в течение 60 мин заявка на пополнение цехового склада до полного объема в 20 комплектов, которая посылается на центральный склад, где в течение 60±20 мин происходит комплектование и за 60±5 мин осуществляется доставка деталей в цех.
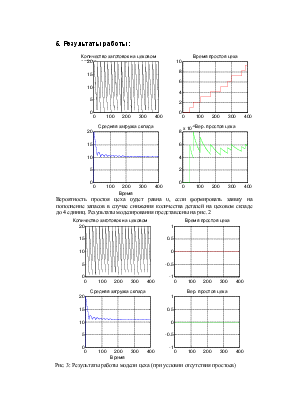
Смоделировать работу цеха в течение 400 ч. Определить вероятность простоя цеха из-за отсутствия деталей и среднюю загрузку цехового склада. Определить момент пополнения запаса цехового склада, при котором вероятность простоя цеха будет равна 0.
Разрабатываемая структура является моделью цеха с вариацией времени обработки детали, времени доставки, и времени комплектования.
Так как в условии задачи ничего не сказано о законах распределения для случайных процессов в системе, то параметры определялись случайной величиной, распределенной по равномерному закону распределения.
Так,
например, для времени обработки детали получено следующее выражение:![]() , где x – случайная
величина, распределенная по равномерному закону на интервале 0…1, а DT = 1/6 – величина
в пределах которой должно изменяться значение случайной величины.
, где x – случайная
величина, распределенная по равномерному закону на интервале 0…1, а DT = 1/6 – величина
в пределах которой должно изменяться значение случайной величины.
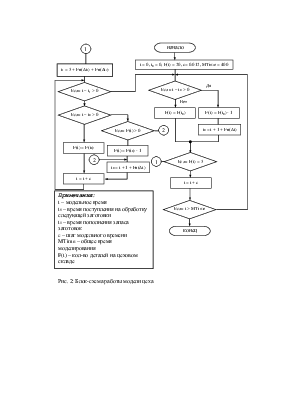
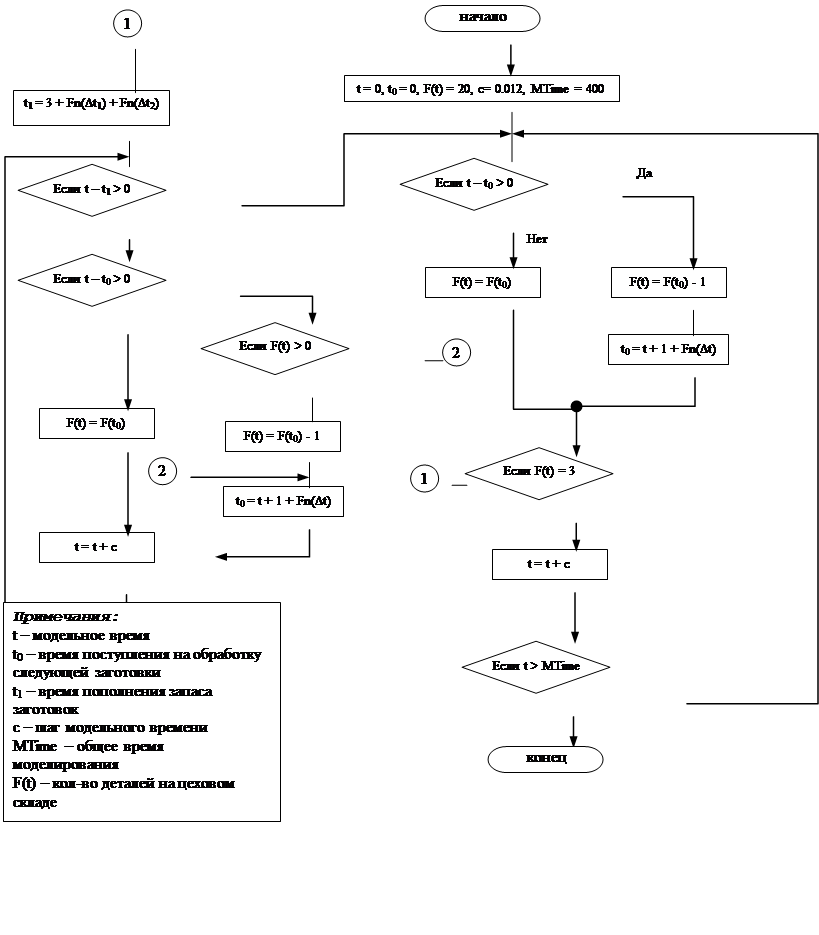
Модель работы цеха показана на рис. 2. Она позволяет отслеживать количество заготовок на цеховом складе, можно фиксировать моменты:
· взятия в работу новой заготовки, при условии окончания обработки предыдущей
· подачи заявки на пополнение цеховых запасов, комплектования нового набора заготовок и доставки его в цех при условии снижения количества заготовок на цеховом складе до критического уровня
· простоев цеха из-за отсутствия заготовок на цеховом складе
 |
||||
|
||||
Для моделирования работы цеха, по алгоритму полученному в п. 2 и в соответствии с заданием, использовался математический пакет MATLAB 5.2. Данный пакет позволяет выполнять:
· числовые и символьные вычисления
· построение графиков функций и процессов любой степени сложности
· построение математических моделей
· программирование, разработка приложений и интерфейсов
В процессе реализации модели были задействованы конструкции и команды пакета MATLAB описанные в таблице 1.
Таблица № 1: Описание использованных команд пакета MATLAB
|
Ключевое слово |
Описание |
|
function [<список выходных переменных>] = <имя функции>(<список входных переменных>) |
- объявление имени функции, входных и выходных переменных |
|
linspace(x1,x2,n) |
- формирует линейный массив размера 1´n, начальным и конечным элементами которого являются точки x1 и x2 |
|
rand() |
- без аргументов данная функция формирует одно случайное число распределенное по равномерному закону, которое изменяется при каждом последующем вызове |
|
while <логическое выражение> <операторы> end |
- цикл while…end выполняется до тех пор, пока значение логического выражения не станет ложным. Логическое выражение имеет форму: выражение <оператор отношения> выражение оператор отношения: ==, <=, >=, <, >, ~ |
|
if <логическое выражение> <операторы> else <операторы> end |
- условное выражение выполняется до тех пор, пока значение логического выражения не станет ложным. Логическое выражение имеет форму: выражение <оператор отношения> выражение оператор отношения: ==, <=, >=, <, >, ~ |
|
break |
- функция break прерывает выполнение цикла while. |
|
subplot(m, n, p) |
- данная команда выполняется перед обращением к функциям построения графиков для одновременной выдачи нескольких графиков в различных частях графического окна; значение m – указывает, на сколько частей разбивается окно по горизонтали, n – по вертикали, а р – номер подокна, куда будет выводится очередной график |
|
plot(x,y) |
- команда plot(x,y) соответствует построению обычной функции, когда одномерный массив х соответствует значениям аргумента, а одномерный массив у – значениям функции |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.