function math()
% Задаем значения погрешностей
Delta1 = 1/6; % Dt возникновения необходимости в новой заготовке
Delta2 = 1/3; % Dt комплектования нового набора заготовок
Delta3 = 1/12; % Dt доставки набора заготовок в цех
Delta_t1 = 0;
T=linspace(0,400,16000); % задаем интервал времени от 0 до 400 часов
% с ценой деления 0,025 часа
F=linspace(0,400,16000); % кол-во заготовок на цеховом складе
AverageCharge=linspace(0,400,16000); % сред. загрузка цехового склада
TimeHold=linspace(0,400,16000); % время простоя цеха
DownTimeProbability=linspace(0,400,16000) % вероятность простоя цеха
i=1; % устанавливаем значение индекса на начало интервала времени
F(i) = 20; % начальное количество заготовок в цехе
TotCharge = 20 % начальная загрузка склада
TimeHold(i)=0;
t1=T(i)+1+rand*Delta1; % момент, когда нам понадобится
% следующая заготовка
DownTimeProbability(i)=0;
while i < 16000,
i = i + 1;
if(T(i)-t1) > 0
F(i)= F(i-1)-1;
TotCharge = TotCharge + F(i);
AverageCharge(i) = TotCharge/i;
t1=T(i) + 1 + rand*Delta1;
Delta_t1 = t1-T(i);
TimeHold(i) = TimeHold(i-1);
DownTimeProbability(i)=TimeHold(i)/i;
if(F(i)) == 3 % если количество заготовок в цехе
% достигло минимально допуст. уровня
% расчитываем время доставки деталей с центрального склада
t2 = T(i)+ 3 + rand*Delta2 + rand*Delta3;
while(T(i)-t2) < 0, % смотрим на разв. событий до момента
% доставки новых заготовок
i = i + 1; % продвигаем время на один щаг
if i > 16000
break;
end
if(T(i)-t1) > 0 % есть необходимость в новой заготовке ?
if(F(i-1)-1) > 0 % если заготовки еще есть
F(i)=F(i-1)-1; % то уменьшаем их кол-во на складе
TimeHold(i) = TimeHold(i-1);
DownTimeProbability(i)=TimeHold(i)/i;
TotCharge = TotCharge + F(i);
AverageCharge(i) = TotCharge/i;
else
F(i)=0; % а если нет то увеличиваем время простоя
TotCharge = TotCharge + F(i);
AverageCharge(i) = Charge/i;
TimeHold(i) = TimeHold(i-1) + Delta_t1;
DownTimeProbability(i)=TimeHold(i)/i;
end
t1=T(i)+1+rand*Delta1;
Delta_t1 = t1 - T(i);
else
F(i)=F(i-1);
TotCharge = TotCharge + F(i);
AverageCharge(i) = TotCharge/i;
TimeHold(i) = TimeHold(i-1);
DownTimeProbability(i)=TimeHold(i)/i;
end
end
F(i)=20;
end
else
F(i)=F(i-1);
TotCharge = TotCharge + F(i);
AverageCharge(i) = TotCharge/i;
TimeHold(i) = TimeHold(i-1);
DownTimeProbability(i)=TimeHold(i)/i;
end
end
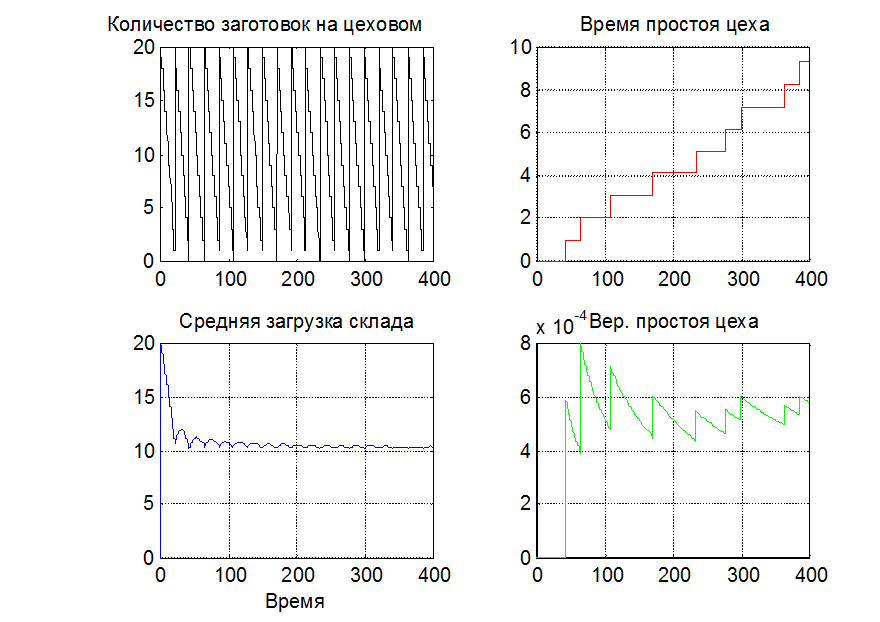
subplot(2,2,1), plot(T,F,'k-');
title('Количество заготовок на цеховом складе');
subplot(2,2,2), plot(T,TimeHold,'r-');
title('Время простоя цеха');
grid on;
subplot(2,2,3), plot(T,AverageCharge,'b-');
title('Средняя загрузка склада');
xlabel('Время');
grid on;
subplot(2,2,4), plot(T,DownTimeProbability,'g-');
title('Вер. простоя цеха');
grid on;
 |
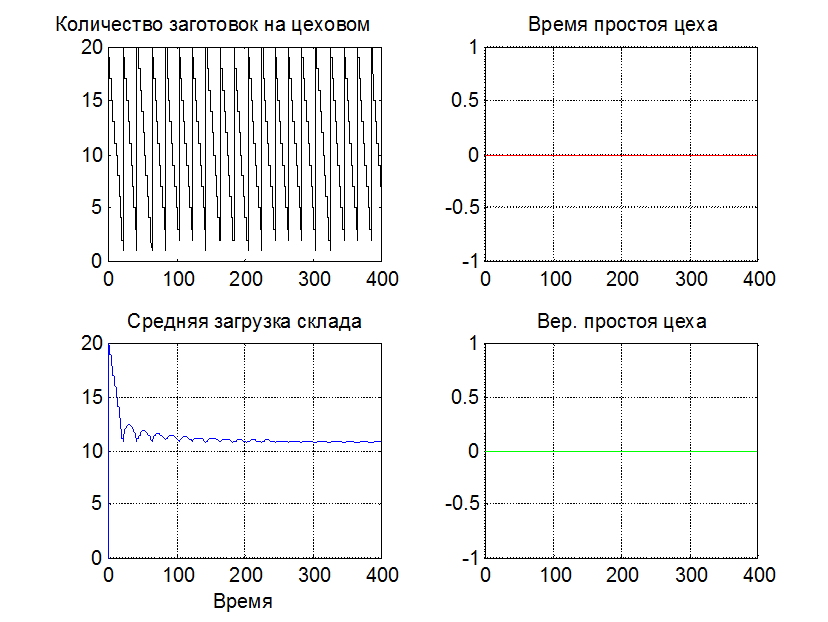 Вероятность
простоя цеха будет равна 0, если формировать заявку на пополнение запасов в
случае снижения количества деталей на цеховом складе до 4 единиц. Результаты
моделирования представлены на рис. 2
Вероятность
простоя цеха будет равна 0, если формировать заявку на пополнение запасов в
случае снижения количества деталей на цеховом складе до 4 единиц. Результаты
моделирования представлены на рис. 2
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.