Циклические коды. Кодер и декодер циклического кода, страница 4

При исследованиях циклического кода широко используется матричная форма представления. Полная образующая матрица циклического кода М^T_n,k= || I^T_k C^T_n-k,k || составляется из двух матриц: единичной транспонированной в канонической форме  I^T_k, соответствующей k информационным разрядам, и дополнительной C^T_n-k,k , соответствующей проверочным разрядам.

Обычно строки дополнительной матрицы определяются путем вычисления многочленов r(х). Для каждой строки матрицы I^T_k  соответствующий остаток r(х) находится делением информационного многочлена а(х) •х^m этой строки на образующий многочлен кода g(x). Дополнительную матрицу можно определить также делением на g(x) комбинации в виде единицы с рядом нулей и использования получающихся остатков в качестве строк дополнительной матрицы. Если степень какого-либо остатка r(х) оказывается меньше (n – k – 1), то следующие за этим остатком строки матрицы получают путем циклического сдвига предыдущей строки

влево до тех пор, пока степень r(х) не станет равной (n – k – 1). Деление производится до получения k строк дополнительной матрицы. Например, для упоминавшегося выше кода (15, 11) с образующим многочленом g (х)= х⁴ + х³ + 1 полная образующая матрица имеет вид:

Аппаратная реализация формирователей циклического кода наиболее просто осуществляется умножением многочлена исходного (информационного) кода на образующий многочлен g(x). Однако такой способ имеет один недостаток: получающиеся в результате умножения комбинации кода не содержат информацион­ных символов в явном виде и для их выделения требуется деление на образующий многочлен. Поэтому на практике используется метод, при котором в выходном коде под информационные символы k отводятся его старшие разряды, а под проверочные (n – k) – младшие. При этом применяется следующая процедура кодирования.

Многочлен а(х), соответствующий k-разрядному входному коду, умножается на х^m, где m = n – k. Степень каждого одночлена, входящего в а(х), увеличивается, что по отношению к комбинации кода означает добавление со стороны младших разрядов т нулей. Затем произведение а(х)•х^m делится на образующий многочлен g(x). В общем случае при этом получается некоторое частное q(x) той же степени, что и а(х), и остаток r(х), который прибавляется к а(х)•х^m. В результате получается многочлен f(x) = а(х)•х^m Å r(х). Поскольку степень g(x) выбирается равной m, то степень остатка r(х) не превышает (m – 1). В комбинации, соответствующей многочлену а(х)•х^m , т младших разрядов нулевые и, следовательно, указанная операция сложения равносильна приписыванию r(х) к а(х) со стороны младших разрядов.

Таким образом, циклический код можно строить, приписывая к каждой комбинации входного кода остаток от деления соответствующего этой комбинации многочлена на образующий многочлен кода. Для кодов, число информационных символов в которых больше числа проверочных, рассмотренный способ реализуется наиболее просто.

Еще один способ кодирования связан с тем обстоятельством, что циклический код является разновидностью группового, что позволяет выражать его проверочные символы через суммы по модулю 2 определенных информационных символов путем решения рекуррентного уравнения 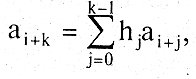 где h_j ^— двоичные коэффициенты так называемого генераторного многочлена h(x) = (хⁿ + l)/g(x). Kaк и в предыдущем случае, проверочные символы размещаются на местах младших разрядов, а при одних и тех же информационных символах комбинации кода совпадают с комбинациями, получающимися при использовании предыдущего способа кодирования. Применение данного способа целесообразно для кодов с числом проверочных символов, превышающим число информационных, например, для кодов БЧХ.

Основой кодирующих и декодирующих устройств циклических кодов являют-