Согласно определению циклического кода все многочлены, соответствующие его кодовым комбинациям, должны делиться на g(x) без остатка. Для этого достаточно, чтобы на g(x) делились без остатка многочлены, которые получаются циклическим сдвигом, что соответствует последовательному умножению g(x) на х с приведением по модулю (хn + 1).
Таким образом, чтобы g (х) мог породить идеал, а следовательно, и циклический код, он должен быть делителем многочлена (хn + 1). Если многочлен g(x) степени m = n – k является делителем (хn + 1), то любой элемент кольца либо делится на g(x) без остатка (тогда он является элементом идеала), либо в результате деления появляется остаток, представляющий собой многочлен степени не выше (m – 1).
Любая принятая по каналу связи кодовая комбинация h(x), содержащая ошибку, может быть представлена в виде суммы по модулю 2 неискаженной комбинации кода f(х) и вектора (кода) ошибки z(x): h(x) = f(x) Å z(x). При делении h(x) на образующий многочлен g(x) остаток, указывающий на наличие ошибки, будет обнаружен только в том случае, если многочлен, соответствующий вектору ошибки, не делится на g(x).
Вектор одиночной ошибки будет иметь единицу в искаженном разряде и нули во всех остальных разрядах. Ему будет соответствовать многочлен z(x) = хi, который не должен делиться на g(x). Остаток от деления любого многочлена на (х + 1) представляет собой многочлен нулевой степени и может принимать только два значения: 0 или 1. Все кольцо в данном случае будет состоять из идеала, содержащего многочлены с четным числом членов, и одного класса вычетов, соответствующего единственному остатку, равному единице. Таким образом, при любом числе информационных разрядов необходим только один проверочный разряд. Значение символа этого разряда как раз и обеспечивает четность числа единиц в любой разрешенной кодовой комбинации, а следовательно, и делимость ее на (х + 1).
Для исправления одиночной ошибки в принятой комбинации из n разрядов необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствует свой класс вычетов и свой опознаватель. Поскольку в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g(x), то g(x) должен обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. При степени многочлена m = n – k он может дать (2n-k – 1) ненулевых остатка (нулевой остаток является опознавателем безошибочной передачи). Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства
2n-k – 1 ≥ n, откуда находится степень образующего многочлена кода m = n – k ≥ log2(n + 1) и общее число символов в кодовой комбинации. Наибольшие значения k и п при различных т можно найти с помощью таблицы, фрагмент которой приведен ниже:
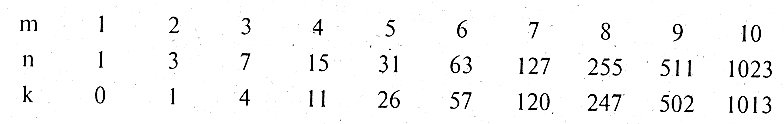
Располагая выбранными значениями m, n и используя таблицы неприводимых многочленов [2], можно выбрать образующий многочлен, после чего необходимо убедиться в том, что он обеспечивает заданное число остатков. Например, при n = 15 и m = 4 в таблице неприводимых многочленов [2] найдем один многочлен первой степени (х + 1), один многочлен второй, степени (х2 + х + 1) и три многочлена четвертой степени: (х4 + х + 1), (х4 + х3 + 1), (х4 + х3 + х2 + х + 1). Перемножив все многочлены, убеждаемся в том, что их произведением является многочлен (х15 + 1) = (хn + 1), т. е. один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Выберем, например, многочлен (х4 + х3 + 1) или 11001 в двоичном коде. Чтобы убедиться, что каждому вектору ошибок соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001, начиная с вектора 00...00001 младшего разряда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.